В настоящее время отсутствует научно-обоснованный подход, учитывающий морфологию рек при принятии проектных решений берегозащитных сооружений. Отсутствуют показатели, позволяющие качественно и количественно оценить правильность принятого проектного решения берегозащитных сооружений, применительно к морфологическим особенностям рек.
Существующие технические решения берегозащитных сооружений нуждаются в дальнейшем совершенствовании и оценке по оптимальному их применению адаптировано к морфологии рек [4,5]. Для создания базы знаний и механизма логического вывода системы поддержки принятия решений требуется алгоритм обработки, который представляет собой разветвленную последовательность логических заключений, выполненных на основании экспертной информации об объекте ранжирования и приводящих к выводу о состоянии этого объекта. Целью исследования является разработка модели ранжирования берегозащитных сооружений, с учетом неполноты исходной информации.
Для решения задачи ранжирования, исходя из имеющихся в наличии исходных данных, пользуются различными методами:
-
последовательного рассмотрения альтернатив по отдельным критериям (лексикографический метод, метод перестановок, метод последовательного сокращения и др.);
-
прямого оценивания альтернатив с использованием заранее заданных оценивающих функций;
-
теории полезности, требующими продолжительного диалога с лицом, принимающим решение, и «подчинения» последнего известной аксиоматике;
-
оценки достижимости целей.
Большинство из перечисленных выше методов приспособлены для решения задач выбора альтернатив при четкой информации. Но небольшая модификация делает их применимыми и в условиях нечеткости.
Ниже представим общую постановку задачи ранжирования сложных техноприродных систем с помощью лексикографического метода.
Пусть заданы или вычислены нечеткие оценки
![]()
множества альтернатив (техноприродных систем)![]() и множества критериев (параметров)
и множества критериев (параметров) ![]() . Необходимо расположить сравниваемые альтернативы в порядке убывания оценки качества по заданным критериям. Будем считать, что критерии упорядочены по важности, например,
. Необходимо расположить сравниваемые альтернативы в порядке убывания оценки качества по заданным критериям. Будем считать, что критерии упорядочены по важности, например, ![]() важнее Х2, Х2 важнее Х3 и т. д.
важнее Х2, Х2 важнее Х3 и т. д.
Суть метода заключается в выделении сначала множества альтернатив с наилучшей оценкой по наиболее важному критерию. Если такая альтернатива одна, то она считается лучшей. Если их несколько, то из подмножества альтернатив, выделенного на предыдущем шаге, выделяются те альтернативы, которые имеют лучшую оценку по следующему критерию в ряду упорядочения их по важности и т. д.
Применение метода при нечеткой исходной информации сводится к следующим действиям:
1. Критерии упорядочить по важности: ![]() .
.
2. С согласия лица, принимающего решения, назначить уровень ![]() , для которого определяется множество лучших альтернатив в соответствии с шагами 3.1-3.3:
, для которого определяется множество лучших альтернатив в соответствии с шагами 3.1-3.3:
3.1. Определить нижнюю ![]() и верхнюю
и верхнюю ![]() границы
границы ![]() -уровневых подмножеств для оценки альтернатив по рассматриваемому критерию [3]:
-уровневых подмножеств для оценки альтернатив по рассматриваемому критерию [3]:
![]() .
.
3.2. Для каждой пары альтернатив ![]() вычислить показатели взаимного превышения критериальных оценок
вычислить показатели взаимного превышения критериальных оценок ![]() и
и![]() :
:
а) если оценки таковы, что ![]() , то
, то
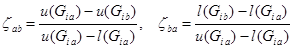 , (1)
, (1)
где ![]() ;
;
б) если оценки пересекаются и ![]() , то
, то
![]() , (2)
, (2)
где ![]() ;
;
в) если оценки не пересекаются и ![]() , то
, то
![]() . (3)
. (3)
3.3.Вычислить показатели ![]() принадлежности l-й альтернативы к множеству лучших (Л-множеству) по i-му критерию
принадлежности l-й альтернативы к множеству лучших (Л-множеству) по i-му критерию
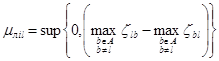 ,
,
где ![]() вычислены по (1) – (3) для i-го критерия.
вычислены по (1) – (3) для i-го критерия.
4. Если Л-множество по рассматриваемому критерию содержит ровно одну альтернативу с ![]() , то она считается лучшей. Если Л-множество содержит более чем одну альтернативу с
, то она считается лучшей. Если Л-множество содержит более чем одну альтернативу с ![]() , то выбирается следующий по важности критерий и повторяются шаги 3.1–3.3. Если все критерии просмотрены и Л-множество содержит более одной альтернативы и
, то выбирается следующий по важности критерий и повторяются шаги 3.1–3.3. Если все критерии просмотрены и Л-множество содержит более одной альтернативы и ![]() <1, то можно увеличить
<1, то можно увеличить ![]() и перейти к шагу 3. Если
и перейти к шагу 3. Если ![]() =1, то окончательный выбор лучшей альтернативы предоставляется лицу, принимающему решение.
=1, то окончательный выбор лучшей альтернативы предоставляется лицу, принимающему решение.
Применение метода при нечеткой исходной информации было использовано для сравнения сложных экологических систем, которыми выступили берегозащитные сооружения. Они сформировали множество альтернатив (техноприродных систем)![]() .
.
Каждую альтернативу сравнивали по следующим критериям: Х1 – надежность; Х2 –эффективность; Х3 – сложность проектирования; Х4 – простота эксплуатации.
Для описания параметров оцениваемых техноприродных систем будем использовать лингвистические переменные, а в качестве их значений – экспертные оценки.
1. В соответствии с алгоритмом на первом шаге упорядочим критерии по важности:
Х2, Х3, Х1, Х4.
2. Назначим уровень α = 0.5, для которого определяется множество лучших альтернатив (Л-множество), на этом этапе оно пустое, т.е. ![]() .
.
Формализация описания критерия техноприродной системы проведем с помощью лингвистической переменной, т.е. кортежа
(β, Т, U, G, M),
где β – название лингвистической переменной;
Т –{«низкая», «средняя», «высокая»};
U= [0, 100] – универсальное множество;
G – процедура, формирующая расширенное терм-множество с помощью элементов множества{«не», «очень», «слегка»};
М – процедура, позволяющая превратить каждое новое значение лингвистической переменной, образуемое процедурой G, в нечеткую переменную.
Пусть β1, β2, β3, β4 – лингвистические переменные с множеством базовых значений (термов) – {низкая, средняя, высокая}. Х=[0,100] – базовое множество [6].
3. Для каждой альтернативы проверим критерий«эффективность», т.е. β1 = «эффективность».
|
Альтернатива |
Экспертная оценка критерия «эффективность» |
|
а1 |
Высокая |
|
a2 |
Средняя |
|
a3 |
Низкая |
|
a4 |
Очень низкая |
а1 = «высокая» = ![]()
a2 =«средняя» = ![]() ;
;
a3 = «низкая» = ![]() ;
;
a4 = «очень низкая» = ![]() .
.
3. 1. Определяем степени включения a2в а1, a3в а1, a4 в а1 по формуле Лукасевича [3]:
![]()
где ![]() = 1& (1-
= 1& (1- ![]() ).
).
а)![]() = (0.5 → 0) & (0.7 → 0) & (0.9 → 0) & (1 → 0) &( 0.9 → 0) &(0.7 → 0) & (0.5 → 0) &(0 → 0.5) &(0 → 0.6) & (0 → 0.9) &( 0 → 1) & ( 0 → 1) = (1 & (1-0.5+0)) & (1 & (1-0.7+0)) & (1 & (1-0.9+0)) & (1 & (1-1+0)) & (1 & (1-0.9+0)) & (1 & (1-0.7+0)) & (1 & (1-0.5+0)) & (1 & (1-0+0.5)) & (1 & (1-0+0.6)) & (1 & (1-0+0.9)) & (1 & (1-0+1)) &(1 & (1-0+1))= 0.5 & 0.3 & 0.1 & 0 & 0.1 & 0.3 & 0.5 & 1 & 1 & 1 & 1 & 1 = 0.
= (0.5 → 0) & (0.7 → 0) & (0.9 → 0) & (1 → 0) &( 0.9 → 0) &(0.7 → 0) & (0.5 → 0) &(0 → 0.5) &(0 → 0.6) & (0 → 0.9) &( 0 → 1) & ( 0 → 1) = (1 & (1-0.5+0)) & (1 & (1-0.7+0)) & (1 & (1-0.9+0)) & (1 & (1-1+0)) & (1 & (1-0.9+0)) & (1 & (1-0.7+0)) & (1 & (1-0.5+0)) & (1 & (1-0+0.5)) & (1 & (1-0+0.6)) & (1 & (1-0+0.9)) & (1 & (1-0+1)) &(1 & (1-0+1))= 0.5 & 0.3 & 0.1 & 0 & 0.1 & 0.3 & 0.5 & 1 & 1 & 1 & 1 & 1 = 0.
Так как ![]() = 0, следовательно
= 0, следовательно ![]() не пересекаются.
не пересекаются.
![]() = 1,
= 1,![]() = 0.
= 0.
б)![]() = (1 → 0) & (0.9 → 0) & (0.7 → 0) & (0.5 → 0) & (0 → 0.5) & (0 → 0.6) & (0 → 0.9) &( 0 → 1) & ( 0 → 1) = (1 & (1-1+0)) & (1 & (1-0.9+0)) & (1 & (1-0.7+0)) & (1 & (1-0.5+0)) & (1 & (1-0+0.5)) & (1 & (1-0+0.6)) & (1 & (1-0+0.9)) & (1 & (1-0+1)) &(1 & (1-0+1))= 0 & 0.1 & 0.3 & 0.5 & 1 & 1 & 1 & 1 &1 &1 = 0.
= (1 → 0) & (0.9 → 0) & (0.7 → 0) & (0.5 → 0) & (0 → 0.5) & (0 → 0.6) & (0 → 0.9) &( 0 → 1) & ( 0 → 1) = (1 & (1-1+0)) & (1 & (1-0.9+0)) & (1 & (1-0.7+0)) & (1 & (1-0.5+0)) & (1 & (1-0+0.5)) & (1 & (1-0+0.6)) & (1 & (1-0+0.9)) & (1 & (1-0+1)) &(1 & (1-0+1))= 0 & 0.1 & 0.3 & 0.5 & 1 & 1 & 1 & 1 &1 &1 = 0.
Так как ![]() = 0, следовательно
= 0, следовательно ![]() не пересекаются.
не пересекаются.
![]() = 1,
= 1,![]() = 0.
= 0.
в)![]() = (1 → 0) & (0.81 → 0) & (0 → 0.5) & (0 → 0.6) & (0 → 0.9) &
= (1 → 0) & (0.81 → 0) & (0 → 0.5) & (0 → 0.6) & (0 → 0.9) &
( 0 → 1) &( 0 → 1) = (1 & (1-1+0)) & (1 & (1-0.81+0)) & (1-0+0.5)) & (1 & (1-0+0.6)) & (1 & (1-0+0.9)) & (1 & (1-0+1)) &(1 & (1-0+1))= 0 & 0.19 & 1 & 1 & 1 & 1 & 1=0.
Так как ![]() = 0, следовательно,
= 0, следовательно, ![]() не пересекаются.
не пересекаются.
![]() = 1,
= 1,![]() = 0.
= 0.
Вычислим показатель ![]() принадлежности l–й альтернативы к множеству лучших (Л –множеству) по первому критерию:
принадлежности l–й альтернативы к множеству лучших (Л –множеству) по первому критерию:
![]() =
= ![]()
![]() =
= ![]() =
= ![]() = 1.
= 1.
3.2. Определяем степени включения a3 в а2, a4 в а2.
а)![]() = (1 → 0) & (0.9 → 0) & (0.7 → 0) & (0.5 → 0) & (0 → 0.5) &
= (1 → 0) & (0.9 → 0) & (0.7 → 0) & (0.5 → 0) & (0 → 0.5) &
(0 → 0.7) & (0 → 0.9) &( 0 → 1) & (0 → 0.9) & (0 → 0.7) &(0 → 0.5) =
(1 & (1-1+0)) &(1 & (1-0.9+0)) & (1 & (1-0.7+0)) & (1 & (1-0.5+0)) & (1 & (1-0+0.5)) & (1 & (1-0+0.7)) & (1 & (1-0+0.9)) & (1 & (1-0+1)) & (1 & (1-0+0.9)) & (1 & (1-0+0.7)) & (1 & (1-0+0.5)) = 0 & 0.1 & 0.3 & 0.5 & 1 & 1 & 1 & 1 & 1 & 1 & 1 = 0.
Так как ![]() = 0, следовательно
= 0, следовательно ![]() не пересекаются.
не пересекаются.
![]() = 1,
= 1,![]() = 0.
= 0.
б)![]() = (1 → 0) & (0.81 → 0) & (0 → 0.5) & (0 → 0.7) & (0 → 0.9) &
= (1 → 0) & (0.81 → 0) & (0 → 0.5) & (0 → 0.7) & (0 → 0.9) &
( 0 → 1) & (0 → 0.9) & (0 → 0.7) &(0 → 0.5) = (1 & (1-1+0)) & (1 & (1-0.81+0)) & (1 & (1-0+0.5)) & (1 & (1-0+0.7)) & (1 & (1-0+0.9)) & (1 & (1-0+1)) & (1 & (1-0+0.9)) & (1 & (1-0+0.7)) & (1 & (1-0+0.5))=0 & 0.19 & 1 & 1 & 1 & 1 & 1 & 1 & 1 = 0.
Так как ![]() = 0, следовательно,
= 0, следовательно, ![]() не пересекаются.
не пересекаются.
![]() = 1,
= 1,![]() = 0.
= 0.
![]() =
= ![]() =
= ![]() = 1.
= 1.
3.3. Определяем степень включения a4 в а3.
![]() = (1 → 1) & (0.81 → 0.9) & (0 → 0.7) & (0 → 0.5) =(1 & (1-1+1)) & (1 & (1-0.81+0.9)) & (1 & (1-0+0.7)) & (1 & (1-0+0.5)) = 1 & 1 & 1 & 1 = 1.
= (1 → 1) & (0.81 → 0.9) & (0 → 0.7) & (0 → 0.5) =(1 & (1-1+1)) & (1 & (1-0.81+0.9)) & (1 & (1-0+0.7)) & (1 & (1-0+0.5)) = 1 & 1 & 1 & 1 = 1.
Так как ![]() = 1, следовательно,
= 1, следовательно, ![]() включено в
включено в ![]() .
.
Определяем нижнюю (l) и верхнюю (u) границы α – уровневых подмножеств для оценки альтернатив по рассматриваемому критерию, т.е. эффективности: l(![]() ) =
) = ![]() ,u(
,u(![]() ) =
) = ![]() .
.
l(![]() ) = 20;u(
) = 20;u(![]() ) = 5;
) = 5;
l(![]() ) = 10; u(
) = 10; u(![]() ) = 5.
) = 5.
![]() =
= ![]() =
= ![]() = 0;
= 0;![]() =
= ![]() =
= ![]() = 0.7
= 0.7
![]() =
= ![]() =
= ![]() = 0.
= 0.
4. Так как Л-множество содержит две альтернативы с ![]() α (т.е.
α (т.е.![]() ), то выбираем следующий по важности критерий и повторяем шаг 3.
), то выбираем следующий по важности критерий и повторяем шаг 3.
Для оставшихся альтернатив проверяем критерий «сложность проектирования».
β2 = «сложность проектирования».
|
Альтернатива |
Оценка критерия «сложность проектирования» |
|
а1 |
Высокая |
|
а2 |
Слегка высокая |
а1 = «высокая»=![]()
а2 =«слегка высокая»={![]() .
.
Определим степень включения a2 в а1.
![]() = (0.55 → 0) & (0.71 → 0.5) & (0.77 → 0.6) & (0.95 → 0.9) & (1 → 1) & (1 → 1) = (1 & (1-0.55+0))& (1 & (1-0.71+0.5)) & (1 & (1-0.77+0.6)) & (1 & (1-0.95+0.9)) & (1 & (1-1+1)) & (1 & (1-1+1)) = 0.45 & 0.79 & 0.83 & 0.95 & 1 & 1 = 0.45.
= (0.55 → 0) & (0.71 → 0.5) & (0.77 → 0.6) & (0.95 → 0.9) & (1 → 1) & (1 → 1) = (1 & (1-0.55+0))& (1 & (1-0.71+0.5)) & (1 & (1-0.77+0.6)) & (1 & (1-0.95+0.9)) & (1 & (1-1+1)) & (1 & (1-1+1)) = 0.45 & 0.79 & 0.83 & 0.95 & 1 & 1 = 0.45.
Так как ![]() = 0.45, следовательно
= 0.45, следовательно ![]() пересекаются.
пересекаются.
l(![]() ) = 80;u(
) = 80;u(![]() ) = 100;
) = 100;
l(![]() ) = 75; u(
) = 75; u(![]() ) = 95.
) = 95.
![]() = 1 -
= 1 -![]() = 1 -
= 1 -![]() = 1 -
= 1 - ![]() = 1 – 0.25 = 0.75
= 1 – 0.25 = 0.75
r(a) = u(![]() ) - l(
) - l(![]() ) = 100 - 80 = 20,r(b) = u(
) = 100 - 80 = 20,r(b) = u(![]() ) - l(
) - l(![]() ) = 95 - 75 = 20.
) = 95 - 75 = 20.
![]() = 0.
= 0.
![]() =
= ![]() =
= ![]() = 0.75.
= 0.75.
Также определим степень включения a1 в а2, для того чтобы определить лучшую альтернативу.
![]() = (0.5 → 0.71) & (0.6 → 0.77) & (0.9 → 0.95) &(1 → 1) & (1 → 1) = (1 & (1-0.5+0.71))& (1 & (1-0.6+0.77)) & (1 & (1-0.9+0.95)) & (1 & (1-1+1)) & (1 & (1-1+1)) = 1 & 1 & 1 & 1 & 1= 1.
= (0.5 → 0.71) & (0.6 → 0.77) & (0.9 → 0.95) &(1 → 1) & (1 → 1) = (1 & (1-0.5+0.71))& (1 & (1-0.6+0.77)) & (1 & (1-0.9+0.95)) & (1 & (1-1+1)) & (1 & (1-1+1)) = 1 & 1 & 1 & 1 & 1= 1.
Так как ![]() = 1, то отсюда следует, что
= 1, то отсюда следует, что ![]() включено в
включено в ![]() .
.
Определяем нижнюю (l) и верхнюю (u) границы α – уровневых подмножеств для оценки альтернатив по рассматриваемому критерию.
l(![]() ) = 80;u(
) = 80;u(![]() ) = 100;
) = 100;
l(![]() ) = 75; u(
) = 75; u(![]() ) = 100.
) = 100.
![]() =
= ![]() =
= ![]() = 0;
= 0;![]() =
= ![]() =
= ![]() = -0.25
= -0.25
![]() =
= ![]() =
= ![]() = 0.25.
= 0.25.
Т.к. ![]() = 0.75 >α, а
= 0.75 >α, а ![]() = 0.25 <α, следовательно, альтернатива а1 считается лучшей и записывается во множество лучших альтернатив Л. Выполняем шаг 4, описанного выше алгоритма, со множеством альтернатив
= 0.25 <α, следовательно, альтернатива а1 считается лучшей и записывается во множество лучших альтернатив Л. Выполняем шаг 4, описанного выше алгоритма, со множеством альтернатив ![]() .
.
Осуществляя, в соответствии с описанным алгоритмом, последовательный перебор всех альтернатив был получен результат. Предложенные альтернативы были упорядочены следующим образом: а1, a2, a3, a4.
Описанный алгоритм лег в основу программного модуля, который является составной частью подсистемы блока управления компьютерной системы управления склоновой эрозией [1,2].
Рецензенты:
Псху А.В., д.ф.-м.н., зав. отделом Дробного исчисления ФГБНУ «Институт прикладной математики и автоматизации», г. Нальчик;
Анахаев К.Н., д.т.н., профессор, заслуженный деятель науки КБР, зам. директора по селевой проблематике ФГБУ «Высокогорный геофизический институт», г. Нальчик.
Библиографическая ссылка
Эдгулова Е.К., Хаширова Т.Ю., Апанасова З.В. МОДЕЛИРОВАНИЕ ЗАДАЧИ РАНЖИРОВАНИЯ БЕРЕГОЗАЩИТНЫХ СООРУЖЕНИЙ В УСЛОВИЯХ НЕПОЛНОТЫ ИСХОДНОЙ ИНФОРМАЦИИ // Современные проблемы науки и образования. – 2014. – № 6. ;URL: https://science-education.ru/ru/article/view?id=16032 (дата обращения: 19.04.2024).



