В данной работе исследуются и оцениваются погрешности расчета температурных полей для тепловой модели плат микроблоков электронной аппаратуры подробно описанной в статьях [1-3]. В частности исследуются погрешности, связанные с дискретизацией, обусловленной применением численных методов расчета.
Цель исследования
Выявление причин появления погрешностей, их оценка и рекомендации по выбору параметров тепловой модели.
Материал и методы исследования
При расчете теплового режима возникают погрешности, связанные с недостоверностью исходных данных и погрешности, обусловленные использованием численных методов, в основу которых положена дискретизация областей расчета.
Недостоверность исходных данных связана с отклонениями реальных значений физических характеристик материалов от декларируемых в справочниках и другой нормативной документации, а также с отклонением размеров и координат размещения элементов конструкции, усилий прижатия поверхностей в пределах допусков, предусмотренных технологиями производства.
В настоящей статье исследуются погрешности, обусловленные применением численных методов решения, то есть погрешности дискретизации области расчета. Анализируется случай, когда плата имеет теплопроводный сердечник и преобладает радиальный отвод тепла.
В зависимости от координат расположения источника тепла количество узлов, попавших на его посадочное место, может изменяться. Это приводит фактически к тому, что его посадочные размеры будут представлены с погрешностью ± 1 узел, что, в свою очередь, приведет к погрешности значения теплового сопротивления «источник тепла – поверхность платы». На рис. 1 показаны примеры вариантов размещения тепловыделяющего элемента относительно узлов сетки.
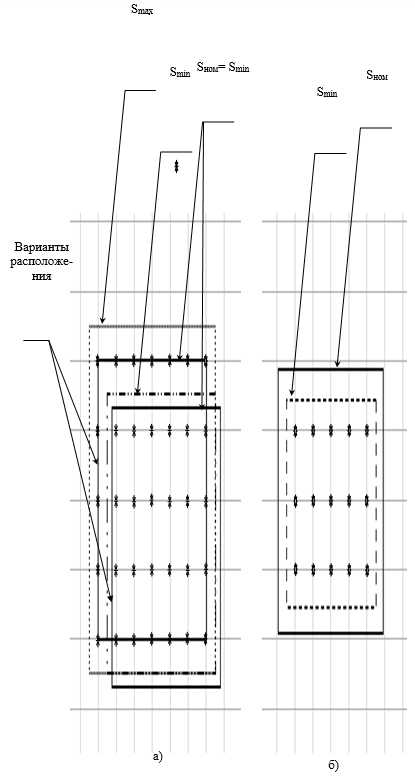
Рис. 1. Варианты расположения посадочной площади источника тепла относительно узлов сетки: а) - размеры a и b кратны шагу сетки и учитываются узлы, попавшие на границу; б) - размеры a и b не кратны шагу сетки.
Рассмотрим общий случай. Пусть источник тепла имеет посадочные размеры: а – ширина, b – длина. Шаг сетки по координатам X и Y будем считать одинаковым и равным Dx. Тогда в зависимости от расположения источника на плате на его посадочную площадь могут попасть как максимум nmax, так и минимум узлов nmin:
![]()
![]() (1)
(1)
![]() , (2)
, (2)
где ![]() - целые части от деления a и b на Dx.
- целые части от деления a и b на Dx.
В случае, когда имеет место nmax, посадочная площадь будет вычислена как Smax= nmax*(Dx)2. В противном случае – как Smin= nmin*(Dx)2. Таким образом, разница при определении посадочной площади может составить DS= Smax- Smin. С учетом выражений (1) и (2):
![]() . (3)
. (3)
После преобразований (3) получим:
![]() (4).
(4).
Анализ выражения (4) показывает, что максимальное значение DS будет иметь в случае, когда размеры a и b кратны Dx, то есть a и b точно делятся на Dx и учитываются узлы, попавшие на границу посадочной площади. На рис. 1 а) представлен этот случай. При этом номинальная площадь Sном=Smin=a*b, а Smax= Sном+ Dx*(a+b)+ (Dx)2. Таким образом, максимальная положительная относительная погрешность вычисления посадочной площади d+max определится по формуле:
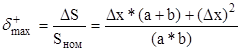 (5).
(5).
Введем коэффициент формы k=b/a и коэффициент ma=a/Dx. Тогда выражение (5) можно преобразовать к виду:
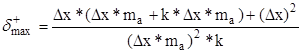 (6).
(6).
Если посадочное поле представляет собой квадрат, то есть k=1, то выражение (6) упрощается:
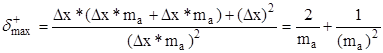 (7).
(7).
График зависимости d+max(ma) приведен на рис. 2. Нетрудно провести математические выкладки, чтобы придти к выводу: максимальная отрицательная относительная погрешность будет иметь место, когда a и b не кратны Dx и выполняется условие (8), что демонстрирует рис.1 б).
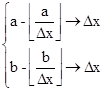 (8)
(8)
В модели, предложенной в [1], эта погрешность исключается простым приемом: при вычислении температурного потенциала между источником тепла и посадочной поверхностью в расчетной формуле используется номинальное значение посадочной площади Sном =a*b. Но необходимо еще учесть отклонение теплового сопротивления Rt теплопроводного сердечника платы от источника тепла до теплостока при изменении размеров источника тепла. Для оценки можно использовать из [4] преобразованную приближенную инженерную формулу (9):
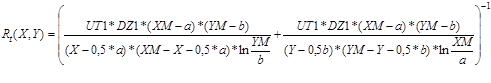 (9),
(9),
где UT1 – коэффициент теплопроводности теплопроводного сердечника платы; DZ1 – толщина теплопроводного сердечника платы; X,Y – координаты центра источника тепла; XM и YM – длина и ширина платы; a и b – ширина и длина источника тепла.
Для случая, когда a=b , a = ma *Dx , XM=YM=D, X=Y=D/2 и D=100*Dx (посадочная площадь источника является квадратом, и он расположен в центре квадратной платы) выражение (9) примет вид:
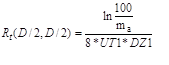 .
.
Наибольшая ошибка при определении посадочной площади источника тепла дает увеличение ее размеров на один шаг сетки, то есть ma увеличится на 1. Так, например, при изменении ma от 10 до 9 тепловое сопротивление Rt изменится в (Rt(ma=9)/Rt(ma=10))=ln(100/9)/ ln(100/10)=1,0457 раз, то есть на 4,57%. Соответственно, на такую же величину изменится температурный перепад на Rt.
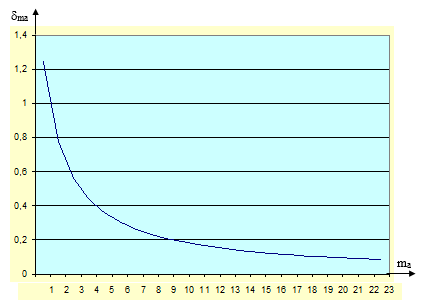
Рис. 2. График зависимости +max(ma).
Результаты исследования и их обсуждение
Для сравнения с приближенными аналитическими оценками был проведен вычислительный эксперимент с помощью пакета прикладных программ расчета температурного поля [2]. Расчеты температурного поля квадратного теплопроводного сердечника были проведены для двух случаев:
- посадочная площадь источника представляет квадрат размером 10´10 узлов и расположена в центре теплопроводного сердечника (в центре платы);
- посадочная площадь источника представляет квадрат размером 9´9 узлов и расположена в центре теплопроводного сердечника (в центре платы).
Мощность, рассеиваемая источником, в обоих случаях была равна 1 ватту, материал сердечника – алюминий, размеры сердечника 94 мм ´ 94 мм ´ 0,25 мм. Шаг сетки по осям X и Y Dx = 1,5 мм, а тепловые сопротивления «сердечник - источник тепла» и «теплосток – сердечник» взяты нулевыми, чтобы получить температурный перепад непосредственно на сердечнике.
Результаты расчета представлены на рисунках 3 и 4. Плоские вершины температурных полей являются следствием усреднения температуры на посадочной площади источника (это заложено в программе). При этом температура теплостока равнялась 25° С. Как видно из рисунков, уменьшение размеров посадочной площади источника тепла на один узел по каждой координате, привело к увеличению перегрева на 0,8 ° С. В первом случае, перегрев составил 40-25=15 градусов, а во втором случае 40,8-25=15,8 градусов.
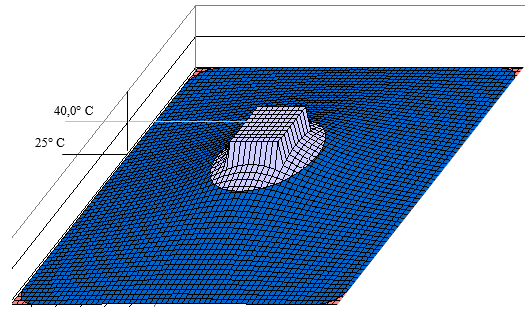
Рис. 3. Температурное поле сердечника при размерах посадочной площади источника тепла 1010 узлов.
Если оценить изменение перегрева в процентах, то получим: (15,8-15)/15´100%=5,3%. Как видим приближенная аналитическая (4,57%) и экспериментальная вычислительная (5,3%) оценки достаточно близки.
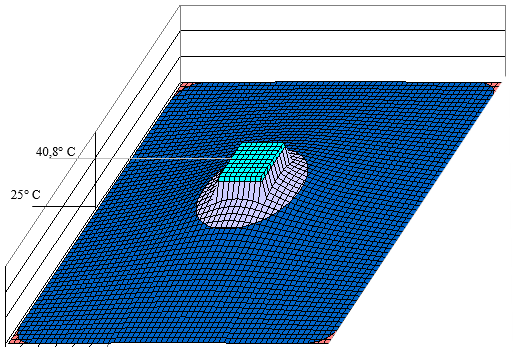
Рис. 4. Температурное поле сердечника при размерах посадочной площади источника тепла 99 узлов.
Выводы
Проведенные исследования позволяют сделать вывод, что ошибки дискретизации при расчете температурных полей зависят от соотношения размеров источников тепла и шага дискретизации. Слишком мелкий шаг дискретизации увеличивает размерность задачи и увеличивает время расчета. Оптимальный выбор шага дискретизации позволяет уменьшить влияние этих ошибок на общую точность расчета. Аналитические оценки и вычислительные эксперименты показали, что выбор шага дискретизации, обеспечивающий попадание 8 – 10 узлов по каждому измерению источников тепла дает ошибку расчета перегрева в районе ±5%. Это вполне приемлемо, так как суммарные ошибки тепловых расчетов, как показывает практика [5], могут достигать 15%.
Рецензенты:
Баламирзоев А.Г., д.т.н., профессор, профессор кафедры Математики и информатики Махачкалинского филиала ФГБОУ ВПО «Московский автомобильно-дорожный государственный технический университет (МАДИ)», г. Махачкала;
Кобзаренко Д.Н., д.т.н., заведующий лабораторией Информационных технологий в энергетике ФГБУН «Институт проблем геотермии ДНЦ РАН», г. Махачкала.
Библиографическая ссылка
Меркухин Е.Н. ИССЛЕДОВАНИЕ ПОГРЕШНОСТЕЙ РАСЧЕТА ДЛЯ ТЕПЛОВОЙ МОДЕЛИ ПЛАТ МИКРОБЛОКОВ ЭЛЕКТРОННОЙ АППАРАТУРЫ // Современные проблемы науки и образования. – 2014. – № 6. ;URL: https://science-education.ru/ru/article/view?id=15864 (дата обращения: 23.04.2024).



