Как известно, задача оптического распознавания символов является трудно формализуемой и имеет множество приближенных методов решений, каждый из которых обладает своими преимуществами и недостатками.
Большинство методов, которые применяются для решения задачи оптического распознавания символов, схожи с методами, которые используются для других задач классификации изображений. Как правило, такие методы предполагают использование искусственных нейронных сетей или аналогичных классификаторов, которые не позволяют отследить логику процесса классификации [5].
Однако существуют методы, специально разработанные для бинаризированных изображений, и, в частности, изображений печатного текста. В таких методах для каждого пиксела известна его принадлежность к начертанию символа или фону. Особую роль среди подобных подходов к решению задачи оптического распознавания символов играет группа методов, основанных на идее анализа пересечений графического представления символа с некоторым набором отрезков. Подобный подход получил название «метод пересечений» [1].
Идею метода пересечений можно интерпретировать огромным количеством способов – можно варьировать набор отрезков, способ геометрического представления символа, правила учета количества и общей длины пересечений каждого из отрезков с этим представлением.
Особый интерес вызывает выбор способа геометрического представления символа. Наиболее простым вариантом можно назвать анализ пересечений символа именно в исходном виде, но такой подход обладает некоторыми недостатками.

Рис.1. Пример нежелательного многократного пересечения отрезка и символа
Для случая, изображенного на рис. 1, характерно многократное пересечение отрезком графического представления символа. Фактически, группа пересекаемых пикселов до растеризации представляла собой отрезок, который не может иметь более одного интервала пересечения. Следовательно, такое представление символа зачастую искажает информацию о пересечениях символа с отрезком.
Наиболее точно описывает геометрию символа лишь его векторное представление. В общем случае символ будет представлен набором графических примитивов, которые будут ограничивать некоторые области изображения. Часть областей будет принадлежать символу, часть – фону.
При подобном представлении символа интервалы пересечения любого отрезка с начертанием этого символа можно определить максимально точно. Но в таком случае возникает проблема высокой вычислительной стоимости анализа интервалов пересечения. Для того чтобы избежать высокой вычислительной сложности и трудной программной реализации, необходимо некоторым образом перевести каждый из отрезков в растровый формат, что приведет к существенному упрощению анализа пересечений. Остается лишь выбрать способ перевода отрезков из векторного формата в растровый.
Описание алгоритма Брезенхэма. Существует множество способов перевести векторный отрезок в растровый формат изображения. Для того чтобы определить, какие пикселы двумерного растра необходимо отнести к изображению отрезка, требуется анализировать их расположение относительно этого отрезка. Джек Е. Брезенхэм в 1962 году предложил способ определения принадлежности каждого из пикселов двумерного растра отрезку с использованием лишь целочисленной арифметики [3].
В ходе алгоритма предполагается проход по каждому значению координат одной из осей и определение значения координаты на другой оси для размещения очередного пиксела.
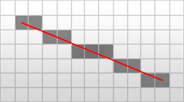
Рис. 2. Иллюстрация работы алгоритма Брезенхэма
Для того чтобы определить наиболее подходящее значение на другой оси координат, необходимо выбрать наиболее близкий к отрезку пиксел двумерного растра. Такую задачу можно решить, используя только целочисленную арифметику, с помощью уравнения прямой в отрезках.
Алгоритм Брезенхэма в методе пересечений. При использовании растрового представления отрезков в методе пересечений анализ интервалов наложения изображения отрезка на изображение символа существенно упрощается. Наиболее простым из допустимых вариантов оценки меры пересечения является тривиальный подсчет количества общих пикселов у двух растровых представлений. В таком случае геометрические потери при растеризации гораздо меньше влияют на результат распознавания. Для более точного описания геометрических потерь можно воспользоваться иллюстрацией.

Рис. 3. Пример геометрических потерь
На рис. 3 оттенками красного цвета показаны пикселы, принадлежащие растеризации изображенного отрезка. Темный оттенок соответствует пикселам, которые относятся к графическому представлению символа, светлый оттенок соответствует остальным пикселам растрового представления отрезка. Как можно заметить, темно-красные пикселы в виду некоторой погрешности растрового представления образуют множество непрерывных интервалов наложения, что при точном геометрическом представлении соответствовало бы лишь одному интервалу наложения. При статистическом подсчете количества общих точек такая погрешность не выглядит столь существенной, сколь может оказаться при более детальном геометрическом анализе. Для приведенного на рис. 3 примера вместо одного интервала наложения можно увидеть сразу пять интервалов, что может привести к затруднениям при проведении анализа количества непрерывных пересечений.
Теперь можно описать алгоритм оптического распознавания символов на основе метода пересечений и алгоритма Брезенхэма.
Шаг 1. Сформировать некоторый набор отрезков.
Шаг 2. Получить растровое представление каждого из отрезков, используя алгоритм Брезенхэма.
Шаг 3. Сформировать набор изображений символов – шаблонов, с которыми будет осуществляться сравнение.
Шаг 4. Для каждого изображения-шаблона произвести наложение каждого из отрезков набора. Для каждого из таких наложений Oi запомнить количество общих пикселей Ci. В дальнейшем вектор значений V = {C1, C2, … , CK} будет использоваться для представления данного изображения – шаблона.
Шаг 5. Для каждого из изображений, класс которого необходимо определить, описанным в шаге 4 образом получить вектор V = {C1, C2, … , CK}. Найти наиболее похожий вектор в наборе шаблонов, определить класс, к которому относится символ, соответствующий этому вектору. Отнести к этому классу данное изображение.
Поиск набора прямых с помощью генетического алгоритма. Задача выбора оптимального набора прямых для решения задачи оптического распознавания символов с использованием метода пересечений является трудно формализуемой и существенно зависит от типа графического представления символов, размеров изображения, а также от набора шаблонных изображений символов.
Одним из способов нахождения оптимального набора прямых является использование генетического алгоритма [2, 4]. Для применения генетического алгоритма необходимо выбрать способ кодирования генетической информации, методы кроссинговера и мутации, способ селекции и функцию приспособленности.
Наиболее простым способом описания прямой являются уравнения прямой с угловым коэффициентом:
![]()
Существенным недостатком такого представления прямой является невозможность описания вертикальной прямой таким образом. Для описанного метода пересечений такой недостаток не критичен, ведь в роли вертикальной прямой может выступать прямая, сколь угодно близкая к вертикальной. При растеризации методом Брезенхэма такая прямая будет неотличима от вертикальной, и, следовательно, можно считать, что уравнение прямой с угловым коэффициентом позволяет задавать прямую для предложенного метода пересечений без потерь. Основным преимуществом такого описания прямой является необходимость хранить лишь два вещественных числа – значения углового коэффициента прямой и свободного члена. Следовательно, хранить набор из n прямых для метода пересечений можно с использованием лишь 2n вещественных чисел.
Как уже ранее было отмечено, хранить набор прямых можно с использованием 2n вещественных чисел. Следовательно, для хранения отдельной особи популяции рационально использовать вещественное кодирование. Для описанного способа вещественного кодирования можно использовать двухточечный или одноточечный операторы кроссинговера. Существенным недостатком двухточечного оператора кроссинговера можно назвать его сравнительно высокую разрушительную способность. Также двухточечный кроссинговер требует чуть более существенных вычислительных затрат. В роли оператора мутации в таком случае может выступать изменение одной из хромосом на некоторую малую величину. Другими словами, в процессе мутации с заданной вероятностью на некоторую небольшую величину может измениться либо угловой коэффициент, либо свободный член одной из прямых набора.
В качестве метода селекции был выбран рулеточный метод селекции, при котором вероятность участия особи в кроссинговере пропорциональна значению его функции приспособленности. В качестве функции приспособленности можно использовать долю успешно распознанных символов некоторого оценочного набора.
Эксперименты и полученные результаты. Изначально для получения оптимального набора прямых был использован генетический алгоритм со следующими значениями параметров:
-
количество особей в популяции равно 16;
-
количество прямых у одной особи равно 8 (16 хромосом);
-
количество эпох эволюции равно 20.
На стадии инициализации начальной популяции был получен набор случайных особей, затем они были отсортированы в порядке убывания значений функции приспособленности. Набор прямых, соответствующий лучшей особи, можно назвать исходным набором прямых. После того, как было осуществлено 20 эпох эволюции, был получен окончательный набор особей, который также был отсортирован по убыванию значений функции приспособленности. Набор прямых, соответствующий лучшей особи, в таком случае можно назвать окончательным набором прямых. На изображении ниже приведены исходные и окончательные наборы прямых для трех различных запусков.
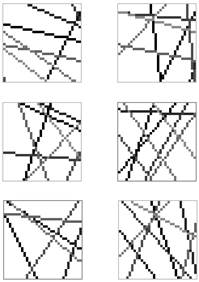
Рис. 4. Исходные (слева) и соответствующие им окончательные (справа) наборы прямых
Аналогичным образом был апробирован генетический алгоритм со следующими значениями параметров:
-
количество особей в популяции равно 32;
-
количество прямых у одной особи равно 16 (32 хромосомы);
-
количество эпох эволюции равно 20.
Исходные и окончательные наборы прямых представлены на рис. 5:

Рис. 5. Исходные (слева) и соответствующие им окончательные (справа) наборы прямых
Выводы. В результате проделанной работы был выявлен ряд закономерностей формирования оптимального набора прямых. По окончании работы генетического алгоритма образуется набор прямых, который заполняет наибольшее количество пространства в центральной области изображения. То есть набор прямых изменяется так, чтобы среднее количество пересечений с начертанием символа было максимально. Важно заметить, что в результате эволюции особи с регулярной структурой не выживают, уступая место особям, у которых интервал различных углов наклона прямых достаточно обширен.
Рецензенты:
Ким В.Л., д.т.н., профессор кафедры вычислительной техники Института Кибернетики ФГБОУ ВПО НИ ТПУ, г. Томск;
Авдеева Д.К., д.т.н., профессор, директор ООО «Медприбор», г. Томск.
Библиографическая ссылка
Хаустов П.А., Спицын В.Г., Максимова Е.И. ГЕНЕТИЧЕСКИЙ АЛГОРИТМ ПОИСКА МНОЖЕСТВА КРИВЫХ ДЛЯ ОПТИЧЕСКОГО РАСПОЗНАВАНИЯ СИМВОЛОВ С ИСПОЛЬЗОВАНИЕМ МЕТОДА ПЕРЕСЕЧЕНИЙ // Современные проблемы науки и образования. – 2014. – № 6. ;URL: https://science-education.ru/ru/article/view?id=15814 (дата обращения: 25.04.2024).



