Рамные конструкции получили широкое распространение в различных отраслях промышленного хозяйства в силу относительной простоты конструктивной формы, влияющей на скорость изготовления и монтажа, а также удобства организации технологических процессов [5].
В зависимости от геометрических параметров (пролет, высота, угол наклона ригеля), а также интенсивности нагружений различают рамы сплошного сечения и решетчатого сечения постоянного и переменного очертания.
При этом расчетным сечением в рассматриваемых рамах является сечение карнизного узла с максимальным изгибающим моментом [1]. В указанном карнизном узле применение сплошного сечения приводит к необоснованному перерасходу материала, а применение решетчатого сечения в наиболее напряженном узле достаточно сложно с позиции трудоемкости изготовления и монтажа.
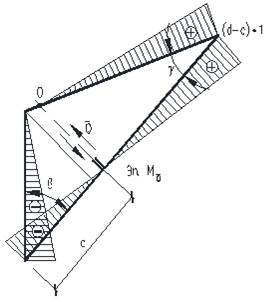
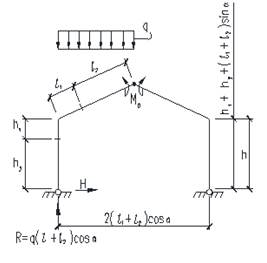
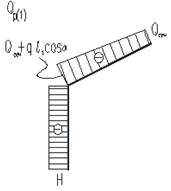
Наиболее рационально применение в указанном узле упрощенного сквозного сечения рамы, включающей стойки, ригели постоянного по длине сечения, и подкосы карнизной части. При этом каждый подкос образован путем продольной резки профилей стыкуемых концов стойки и ригеля с последующим отгибом их нижних частей и соединенных между собой, например, на болтах [2] (рис. 1).
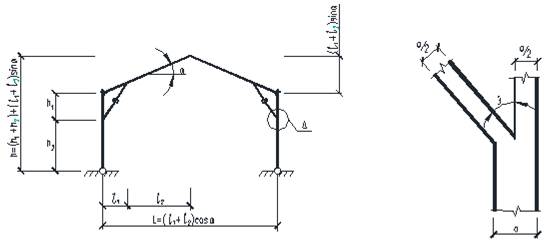
Рис. 1. Геометрическая схема рамы и узла
Постановка задачи
Рассматриваемая рама изготовлена из однотипного профиля. При этом в наиболее напряженном (карнизном) узле имеет развитое поперечное сечение, что позволяет воспринимать большие усилия. По статической схеме рама является статически неопределимой как внешне, так и внутренне, и для изучения работы рамы необходимо получить аналитические зависимости распределения внутренних усилий в ее элементах.
Решение задачи
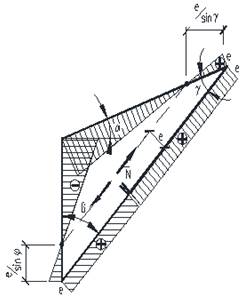
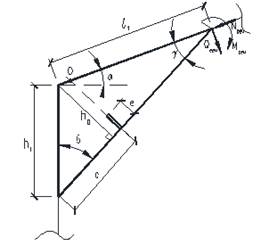
Для решения задачи использован суперэлементный подход с реализацией метода сил [3, 4], поскольку рама регулярна и осесимметрична, имея в своем составе замкнутый контур. При этом рама разбита на подконструкции в виде треугольного замкнутого суперэлемента (рис. 2) и элемент стойки и ригеля.
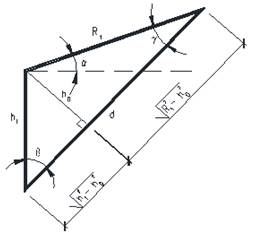
Рис. 2. Геометрическая схема “суперэлемента”
Канонические уравнения для “суперэлемента” записаны методом сил, используя предпосылки упругого линейного расчета, геометрических условий при 
; 
и следующего правила знаков:
а) Осевая сила “+N” – растяжение; “-N” – сжатие;
б) Перерезывающая сила “+Q” – если отсеченная часть вращается по часовой стрелке, либо ось вращения до совмещения с эпюрой “М” по часовой стрелке.
в) Изгибающие моменты: “-М” – для левой части против часовой стрелки; “+М” – для правой по часовой стрелке.
Геометрические соотношения для “суперэлемента” записаны в виде:
;
, то есть 
;
или 
.
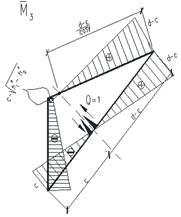
Определение характера распределения эпюры моментов внутри “суперэлемента” выполнено за счет введения “фиктивных” консолей с приложением к ним единичной усилий 
(рис. 3).
В частности, для сдвигающего усилия 
из условия равенства нулю суммы площадей эпюры моментов, определено расстояние “с”, характеризующего положение консоли по длине подкоса (рис. 3).
Исходя из соотношения площадей:
1. 
2. 
и геометрических параметров элемента:
, 
|
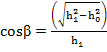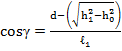
а)
|
б)
|
Рис. 3 Схема распределения изгибающих моментов в “суперэлементе” от единичных усилий.
(а) и 
.
получено:
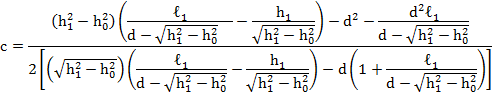
Аналогично для 
1. 
2. 
Эксцентриситет приложения усилия :
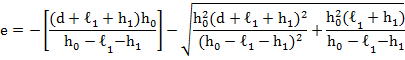
Каноническое уравнение метода сил для контура без консолей можно записать в виде:
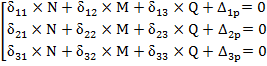
При наличии консолей:
тогда:
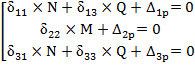
или:
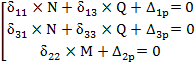
По правилу Крамера для первых двух уравнений:
(1) 
Для третьего:
(2) 
(3) 
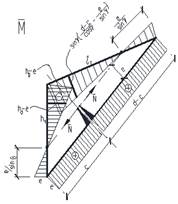
Определение перемещений для замкнутого контура в месте рассечения (пренебрегая перемещениями от усилий Q) – первое неизвестное (рис. 4)
|
|
|
|
Рис. 4. К определению перемещений от единичных усилий
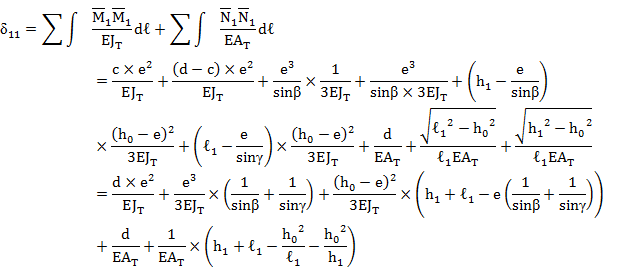
- второе неизвестное (рис. 5)
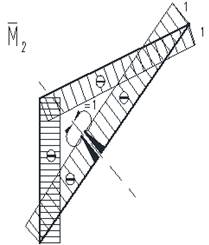
Рис. 5. К определению перемещений от единичной нагрузки
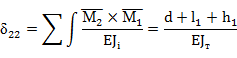
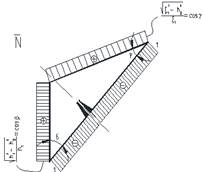
- третье неизвестное (рис. 6)
|
|
|
|
Рис. 6. К определению перемещений от единичной нагрузки
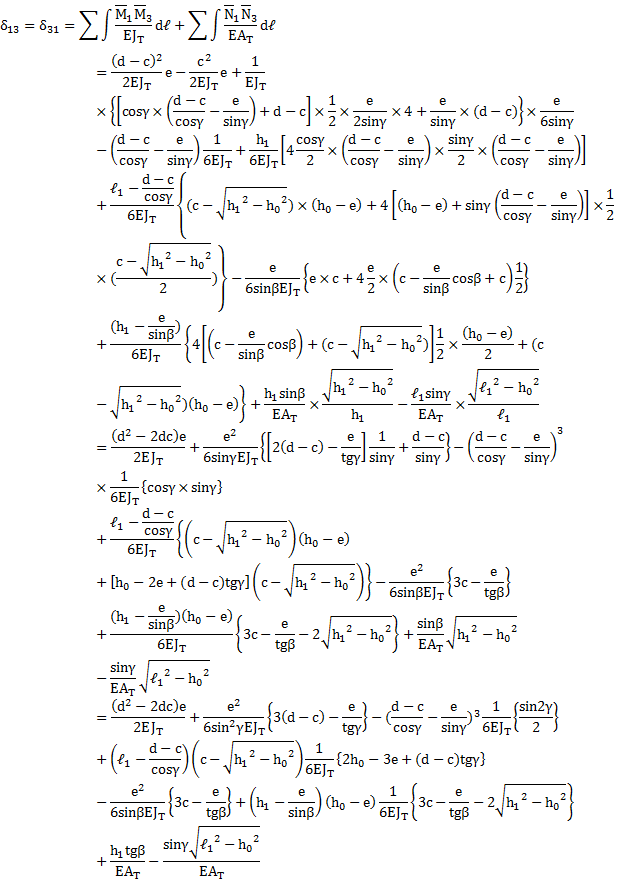
В качестве внешнего воздействия на основную систему рассмотрено загружение рамы (включая “суперэлемент”) равномерно-распределенной нагрузкой “q” (рис. 7) при условии полученного решения на границах контура.
|
|
|
Рис. 7. Вариант загружения основной системы равномерно-распределенной нагрузкой
Исходя из условия равновесия:
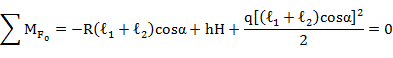
получим распор рамы (рис. 8):
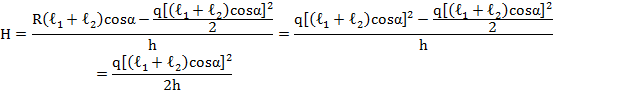
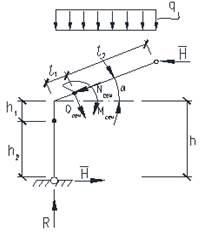
Рис. 8. Расчетная основная схема для определения внутренних усилий от равномерно-распределенной нагрузки
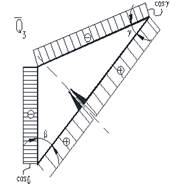
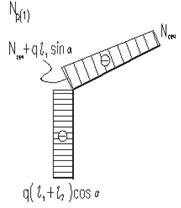
Эпюры внутренних усилий в “суперэлементе” при действии внешней нагрузки, приведены на рис. 9
|
|
|
|
Рис. 9. Эпюры внутренних усилий в “суперэлементe“ при действии нагрузки “q“
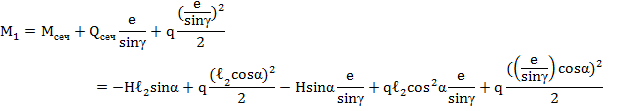
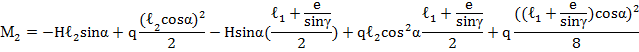
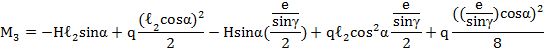
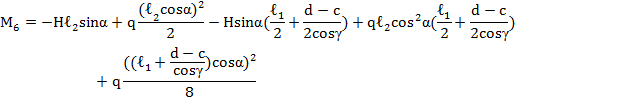
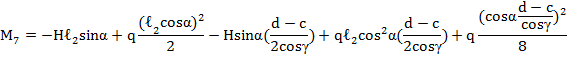
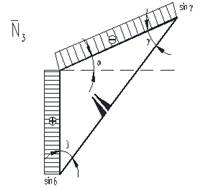
В случае загружения основной системы (ОС) единичной нагрузкой (распор Рис. 10) получим решение в следующем виде:
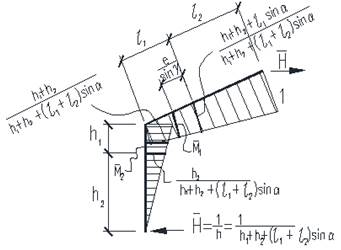
Рис. 10. Загружение ОС единичной нагрузкой распора
Таким образом:
Решение для «супер элемента» по 1 случаю (загружение основной общей системой внешней нагрузкой).
Внутренние усилия в месте рассечения:
(
Решение для «супер элемента» по 2 случаю (загружение общей основной системы единичной нагрузкой):
(
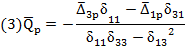
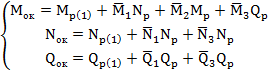
Окончательные эпюры для «супер элемента» по второму случаю
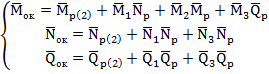
Для общей основной системы, учитывая рассмотренные варианты загружений, записано каноническое уравнение в виде:
, где 
.
Определение неизвестных выполнено методом сил, пренебрегая компонентами перерезывающих усилий (в силу малости и упрощения задачи), при учете распределения внутренних усилий в «суперэлементе» от действия единичной силы (единичное состояние по рис. 10) и внешней нагрузки на ригель рамы (грузовое состояние по рис. 9).
, 
.
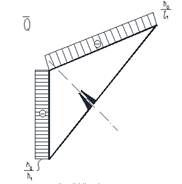
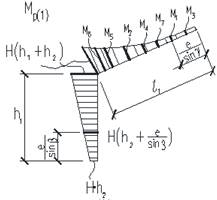
Характер эпюр распределения моментов, полученных на основе решения, в общей основной системе, приведены на рис. 11.
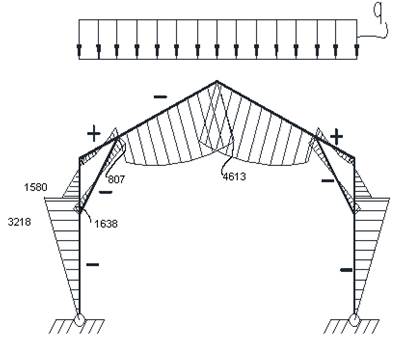
Рис. 11. Эпюры распределения моментов
Рассмотрим пример определения внутренних усилий в раме при действии равномерно-распределенной нагрузки q=2000кг/м, соответствующей сочетанию нагрузок от собственного веса (g=600кг/м) и снеговой (g=1400кг/м). Геометрические параметры рамы: L=6м, l1=1.2м, h1=1м, h0=0.71м, d=1.71м, α=150.
Положение консоли, определяемое по уравнению равновесия внутренних эпюр моментов от фиктивной перерезывающей силы: с=0.834м, а величина консоли е=-0.212м. Распределение внутренних усилий в «суперэлементе» приведено на рис. 6, где значения неизвестных от единичных усилий составляют: δ11=8,8*104, δ22=1,5*106, при усилии распора от внешней нагрузки H=2016кг.
Значения изгибающих моментов на участке l1 (по длине «суперэлемента») от «грузового состояния» (рис. 9):
М1=3024кгм, М2=3152кгм, М3=2613кгм, М4=3339кгм, М6=3890кгм, М7=2611кгм.
При этом в уровне карниза момент: 
, а значения усилий на границах «суперэлемента» (рис. 8) составляют:
,
,
,
Характер распределения моментов от единичного распора, приведен на рис. 10, где значения моментов в карнизном узле от «единичного состояния»:
,
а значения усилий на границах «суперэлемента» (рис. 10) составляют:
, 
,
Окончательный результат, получаемый перемножением эпюр «единичного» и «грузового» состояния, приведен на рис. 11.
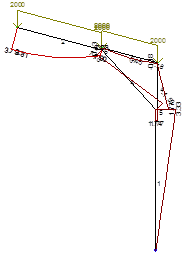
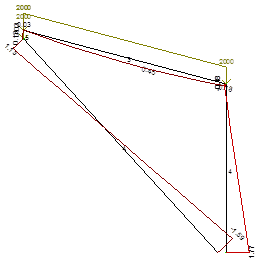
Рассматривая аналогичную расчетную схему, реализованную в виде конечно-элементной стержневой системы в ВК «ЛИРА», получено качественное и количественное совпадение эпюр внутренних усилий (рис. 12) с точностью 3-20%, что объясняется упрощением точного решения.
При этом точное решение, не смотря на трудоемкость математического аппарата, позволяет установить аналитические зависимости, такие как влияние геометрических параметров на весовые показатели рамы.
|
|
|
Рис. 12. Характер и значения изгибающих моментов (тн·м) для рамы
Рецензенты:
Кузнецов И.Л., д.т.н, профессор, заведующий кафедрой «Металлических конструкций и испытаний сооружений» ФГБОУ ВПО «Казанский государственный архитектурно-строительный университет», г. Казань.
Каюмов Р.А., д.ф-м.н., профессор, профессор кафедры «Механики» ФГБОУ ВПО «Казанский государственный архитектурно-строительный университет», г. Казань.
Библиографическая ссылка
Вахтель Р.Р., Исаев А.В., Ефимов О.И., Закиров Р.А. К РАСЧЕТУ РАМЫ С РАСЩЕПЛЕНИЕМ СЕЧЕНИЯ В УРОВНЕ КАРНИЗНОГО УЗЛА // Современные проблемы науки и образования. – 2014. – № 6. ;URL: https://science-education.ru/ru/article/view?id=15704 (дата обращения: 20.04.2024).