При построении популярных блоковых помехоустойчивых кодов (Боуза – Чоудхори –Хоквингема (БЧХ-кодов), Рида – Соломона) используются полиномы Жегалкина. БЧХ-коды [4] имеют чёткие рекомендации выбора образующего полинома, но такие коды ограничены фиксированной длиной кодового слова. Остальные длины кодовых слов получаются путём укорачивания более длинных кодовых слов за счёт уменьшения разрядности информационного блока при сохранении количества контрольных разрядов. Укорачивание БЧХ-кодов вводит лишнюю избыточность, которая не несёт в себе дополнительных корректирующих возможностей, а лишь уменьшает эффективность кода. При поиске образующих полиномов, необходимых для построения кодов, более эффективных, чем укороченные БЧХ-коды, известны только необходимые начальные условия для поиска, такие как минимальные вес образующего полинома, минимальная длина кодового слова, а значит, и минимальная длина образующего полинома. Для того чтобы найти подходящий полином, необходимо перебрать все полиномы, подходящие под выше озвученные необходимые условия, и, если среди них не найдётся полином, который будет удовлетворять достаточным условиям, то поиск продолжится среди полиномов, длина которых на единицу больше, чем предыдущих [5]. В связи с приведёнными необходимыми и достаточными условиями задача по поиску образующего полинома является достаточно трудоёмкой. Таким образом, чтобы значительно ускорить выполнение данной задачи, следует применять технологии параллельных и распределённых вычислений.
Алгоритм поиска образующих полиномов
Алгоритм поиска образующих полиномов заключается в полном переборе всех полиномов – претендентов и проверке их на выполнение достаточных [1, 5] условий, что является ресурсоемкой задачей. Среди достаточных условий образующего полинома являются два основных: 1) строящийся на основе этого образующего полинома код должен иметь расстояние Хэмминга не меньшее, чем d=2t+1; 2) остатки от деления всех комбинаций ошибок на образующий полином в рамках заданной t должны быть уникальными. Полное описание алгоритма поиска образующих полиномов приведено в [5].
Для поиска образующего полинома задаются входные параметры, такие как: разрядность информационного блока (m) и количество исправляемых независимых ошибок (t). Выходным значением является образующий полином в двоичном представлении.
При анализе алгоритма поиска образующего полинома было установлено, что при больших значенияx входного параметра m значительное время работы алгоритма занимает вычисление расстояния Хэмминга помехоустойчивого кода, а также при увеличении значений входного параметра t увеличивается время проверки синдромов на уникальность.
Для анализа возможности распараллеливания программа была условно разбита на 2 этапа, с замером времени выполнения для каждого этапа. Первым этапом является проверка расстояния Хэмминга, второй этап – проверка синдромов ошибок на уникальность. Анализ алгоритма показал, что при поиске образующего полинома практически все полиномы-кандидаты проходят через первый этап, в то время как через этап проверки синдромов на уникальность проходит 1–2 полинома, которые, как правило, являются образующими. Таким образом, в данном алгоритме этап проверки расстояния Хэмминга требует временных затрат за счет большого количества проверяемых полиномов, в то время как второй этап требует временных затрат для проверки каждого полинома из множества [6].
Из анализа можно сделать вывод, что для достижения наилучшей оптимальности следует использовать технологию MPI в совокупности с OpenMP. Так, технологию OpenMP с распараллеливанием вычислений на потоки можно в данном случае применить для оптимизации этапа проверки синдромов на уникальность, а технология MPI позволит оптимизировать этап проверки расстояния Хэмминга за счет распределения большого числа проверяемых полиномов на группы для уменьшения области перебора.
Применение технологий OpenMP и MPI для поиска образующего полинома
Для увеличения быстродействия поиска образующего полинома были применены технологии параллельных и распределённых вычислений, такие как OpenMP [2] и MPI [3]. С использование технологии OpenMP был оптимизирован этап проверки синдромов ошибок на уникальность [1]. При использовании технологии MPI осуществляется межпроцессорный обмен полиномами заданной длины и веса в распределённой системе (суперкомпьютерный кластер) [7]. Главный процессор с помощью команды MPI_Send пересылает списки полиномов другим процессорам, которые принимают данные с помощью команды MPI_Recv и осуществляют поиск образующего полинома среди принятого набора. В случае если среди полиномов заданной длины и веса образующий полином не найден, то согласно алгоритму поиска [5] увеличивается вес полинома, и обмен сообщений между процессорами повторяется. Если же вес полинома становится равным его длине, а полином не найден, то длина полинома-кандидата увеличивается на единицу и поиск осуществляется среди нового набора кандидатов. На рис. 1 приведена схема применения технологий OpenMP и MPI для задачи поиска образующего полинома.
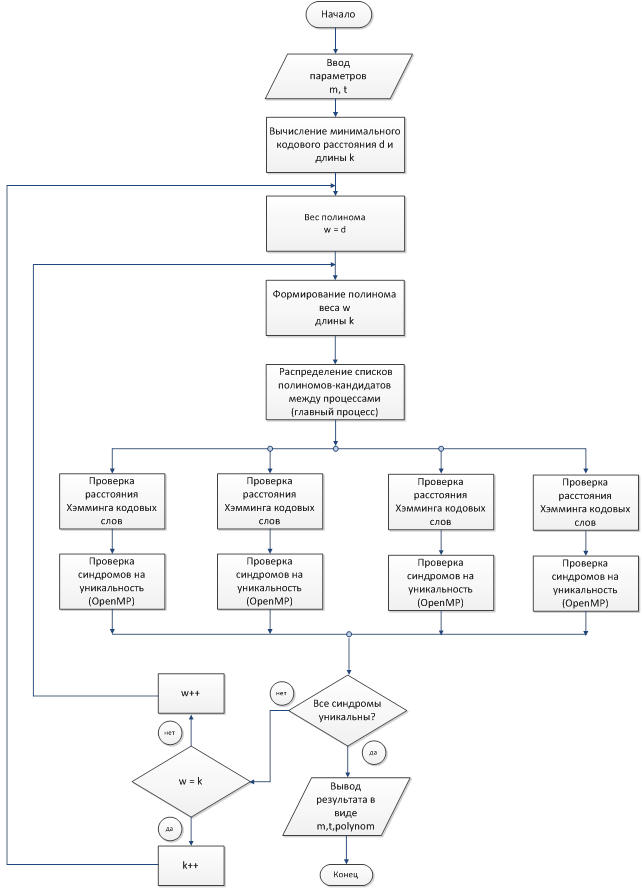
Рис. 1. Схема применения OpenMP и MPI для поиска образующего полинома
Результаты компьютерного эксперимента по поиску образующих полиномов
Для получения статистики по времени поиска образующих полиномов было произведено по 20 запусков исполняемого файла программы, разработанной с применением технологий OpenMP и MPI, на процессорах Intel XEON 5150 2.66Ghz. Для компьютерного эксперимента входной параметр m (длина информационного блока) был выбран в диапазоне от 16 до 24, а параметр t (кратность исправляемых ошибок) равным 3 и 4.
Далее представлены результаты по времени поиска образующего полинома с применением технологии MPI при использовании 30 ядер процессора Intel XEON 5150 в распределённой системе (суперкомпьютерный кластер). В таблице 1 приведены средние значения по времени поиска образующего полинома (с доверительными интервалами) с применением технологий OpenMP и MPI на 30 ядрах процессора Intel XEON 5150 2.66Ghz.
Таблица 1
Средние значения по времени поиска образующего полинома с применением OpenMP и MPI для t = 3 с доверительными интервалами в %
|
m, t |
Исходный, с, (%) |
MPI + OpenMP (30 ядер), c, (%) |
Ускорение, % |
|
16,3 |
1,8 (±0,7) |
0,5 (±2,4) |
247,5 |
|
17,3 |
15,9 (±0,2) |
1,8 (±3,2) |
774,8 |
|
18,3 |
16,4 (±0,1) |
2,4 (±2,7) |
562 |
|
19,3 |
82,7 (±0,2) |
8,8 (±2,8) |
839,9 |
|
20,3 |
261,8 (±0,03) |
20,8 (±1,1) |
1157,5
|
|
21,3 |
267,3 (±0,4) |
24,4 (±0,9) |
994,5 |
|
22,3 |
283,1 (±0,05) |
31,1 (±2,1) |
808,7 |
|
23,3 |
402,5 (±0,04) |
42,9 (±1,4) |
837,6 |
|
24,3 |
678,2 (±0,2) |
76,05 (±0,1) |
791,8 |
Для наглядного представления результатов на рис. 2 приведён график столбца «Ускорение» из таблицы 1.
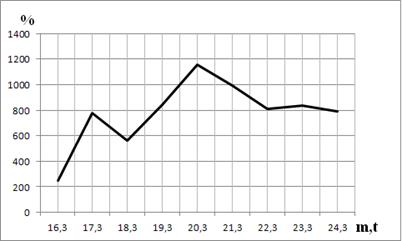
Рис. 2. Ускорение поиска полинома с применением MPI для t = 3 (30 ядер)
В данном случае максимальное ускорение составляет 1157 % (m=20,t=3), что незначительно больше, чем при использовании 20 ядер кластера. В среднем ускорение составляет 779 %. В таблице 2 представлены результаты по времени поиска полинома с применением OpenMP и MPI для t = 4.
Таблица 2
Средние значения по времени поиска образующего полинома с применением OpenMP и MPI для t = 4 с доверительными интервалами в %
|
m, t |
Исходный, с, (%) |
MPI + OpenMP (30 ядер), c, (%) |
Ускорение, % |
|
16,4 |
300,4 (±1,2) |
6,3 (±0,1) |
4599,8 |
|
17,4 |
436,5 (±1,6) |
10,1 (±1,5) |
4212,3 |
|
18,4 |
484,4 (±0,6) |
10,5 (±0,5) |
4509,9 |
|
19,4 |
566,5 (±1,2) |
11,5 (±0,5) |
4814 |
|
20,4 |
640,3 (±0,7) |
13,3 (±0,1) |
4683,2 |
|
21,4 |
736,9 (±0,4) |
17,4 (±0,2) |
4121,6 |
|
22,4 |
12173,9 (±0,7) |
380,9 (±0,08) |
3095,3 |
|
23,4 |
37043,4 (±0,5) |
1479,3 (±0,3) |
2404 |
|
24,4 |
38634,8 (±0,5) |
1570,4 (±0,1) |
2360 |
Для наглядного представления результатов на рис. 3 приведён график столбца «Ускорение» из таблицы 2.
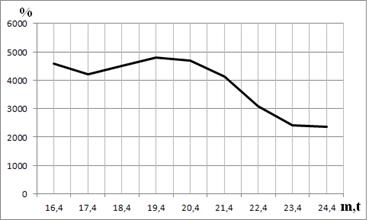
Рис. 3. Ускорение поиска полинома с применением MPI для t = 4 (30 ядер)
В данном случае при t = 4 ускорение варьируется от 2360 % до 4814 %, что является довольно высоким показателем (от 24 до 49 раз). В среднем ускорение составляет 3866 %, т.е. для заданных входных параметров при использовании 30 ядер суперкомпьютерного кластера время поиска образующего полинома уменьшается до 40 раз.
Заключение
В данной работе было рассмотрено применение технологий параллельных и распределённых вычислений для выполнения трудоёмкой задачи по поиску образующих полиномов. При использовании 30 ядер суперкомпьютерного кластера (что являлось максимально доступным для эксперимента) в среднем ускорение составляет 779 % при t = 3 и 3866 % при t = 4, то есть для заданных входных параметров время поиска образующего полинома уменьшается до 8 и 40 раз соответственно. Данные результаты показывают, что относительное быстродействие увеличивается при повышении трудоёмкости задачи. Данный факт позволяет применять программу, разработанную с использованием технологии MPI для поиска образующих полиномов, участвующих в построении помехоустойчивых кодов, исправляющих ошибки большой кратности. В целом полученные результаты эксперимента говорят о том, что, применяя технологии OpenMP и MPI, можно ускорить выполнение такой трудоёмкой задачи, как поиск образующего полинома до 40 раз и более в зависимости от длины информационного блока, кратности исправляемых ошибок и используемых ядер распределённой системы.
Работа выполнена в рамках ФЦП «Исследования и разработки по приоритетным направлениям развития научно-технологического комплекса России на 2014–2020 годы». Государственный контракт № 14.578.21.0032.
Рецензенты:
Авдеева Д.К., д.т.н., профессор, директор ООО «Медприбор», г. Томск.
Ким В.Л., д.т.н., профессор кафедры вычислительной техники Институт кибернетики, ВГАОУ ВО НИ ТПУ, г. Томск.
Библиографическая ссылка
Мыцко Е.А., Мальчуков А.Н. ПРОГРАММНАЯ РЕАЛИЗАЦИЯ АЛГОРИТМА ПОИСКА ОБРАЗУЮЩИХ ПОЛИНОМОВ С ПРИМЕНЕНИЕМ ТЕХНОЛОГИЙ OPENMP И MPI // Современные проблемы науки и образования. – 2014. – № 6. ;URL: https://science-education.ru/ru/article/view?id=15685 (дата обращения: 25.04.2024).



