Создание российских государственных корпораций (ГК) преследует цель совершенствования экономического механизма развития промышленности в соответствующих секторах. [1,2,4,6] Решение задачи идентификации состояния ГК требует нахождения их функций принадлежности (ФП) к выделенным классам. Например, госкорпорации можно относить к «мало эффективным», «стабильно функционирующим», «высоко эффективным» хозяйствующим субъектам. Число классов, их сущностное содержание определяет эксперт, лицо, принимающее решение (ЛПР), исходя из сформулированной задачи управления ГК.
Если удастся решить задачу принадлежности ГК к выделенным классам в каждый конкретный момент времени в зависимости от значений характеризующих их признаков, то тем самым можно будет отследить и спрогнозировать динамику изменения состояния корпорации в заданном признаковом пространстве, и рассчитать необходимые изменения параметров функционирования для перевода ГК в нужное состояние.
В связи с вышесказанным, целью исследование является попытка объединения статистических методов, содержащих достаточно репрезентативную информацию, и теории нечетких множеств, использующей интуитивные механизмы, которые содержат слишком высокий уровень субъективизма исследователя. Что позволит максимально использовать данные наблюдений для формирования и коррекции гипотез ЛПР.
Материалы и методы исследования. Для исследования и иллюстрации применения разрабатываемых механизмов и моделей выбрано четыре российские госкорпорации: РОСНАНО, РОСТЕХ, ОАК и РОСАТОМ, обозначенные далее соответственно: Н, Т, О и А. В качестве признаков, характеризующих их эффективность, в связи с учетом ключевых задач госкорпораций (получение дохода от производственной деятельности, инновационное развитие перспективных проектов в соответствующей отрасли) выбраны: доход от продажи производимых продуктов на одного штатного работника (переменная х1) и расходы от инвестиционной деятельности, также приведенные в одной штатной единице (переменная х2). Всего анализировалось 35 характеристик госкорпораций [7,8,9,10]. Обозначенные выше исходные данные сведены в таблицу 1.
Таблица 1
Исходные данные для расчетов [7,8,9,10]
|
Признаки госкорпораций, (тыс. р) |
Н |
Т |
О |
А |
|
х1 |
434,3 |
8955,5 |
22195,2 |
251,6 |
|
х2 |
818,7 |
2076,5 |
1690,1 |
2582,7 |
Согласно положениям теории нечетких множеств, для определения функции принадлежности [3, 5] можно использовать уже известные данные о структурных особенностях и специфики функционирования объекта, кроме этого в основе определения может лежать мнение группы выбранных экспертов. Так же, в качестве частного случая, данную функцию можно определить статистическими приемами, при котором функция принадлежности вполне может явиться функцией распределения случайной величины.
В первом случае в силу полной априорной определенности задача построения ФП не стоит. Второй случай требует репрезентативной (статистически однородной, стационарной, достаточной по объему) информации, которой, как правило, в рассматриваемой сфере нет (ГК функционируют еще в очень коротком периоде, в неопределенной и нестационарной среде). Поэтому рассматривать статистические методы идентификации ФП нецелесообразно.
Далее целесообразным представляется осуществить построение функции принадлежности на основе привлечения экспертов, а именно функции принадлежности
![]() элементов Х некоего пространства, выбранного в качестве базового, к нечеткому множеству А [3,5]. Решение указанной задачи может быть достигнуто, если эксперты напрямую установят весовые коэффициенты. Для этого можно привлекать одного эксперта или создавать экспертную группу. Но это не является единственным возможным вариантом. В результате решения некоторых смежных задач может быть получено опосредованное определение информативности. Для примера рассмотрим случай работы с группой экспертов, в количестве n, которые должны определить принадлежность некоего элемента Х (показатель, характеризующий ГК) расплывчатому множеству А (например, множеству мало эффективных ГК). Предположим, что ответ «
элементов Х некоего пространства, выбранного в качестве базового, к нечеткому множеству А [3,5]. Решение указанной задачи может быть достигнуто, если эксперты напрямую установят весовые коэффициенты. Для этого можно привлекать одного эксперта или создавать экспертную группу. Но это не является единственным возможным вариантом. В результате решения некоторых смежных задач может быть получено опосредованное определение информативности. Для примера рассмотрим случай работы с группой экспертов, в количестве n, которые должны определить принадлежность некоего элемента Х (показатель, характеризующий ГК) расплывчатому множеству А (например, множеству мало эффективных ГК). Предположим, что ответ «![]() », дали n1 экспертов, а другие n2 = n – n1, отвечают что «
», дали n1 экспертов, а другие n2 = n – n1, отвечают что «![]() ». Тогда следует:
». Тогда следует:
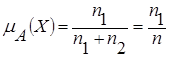 . (1)
. (1)
Пример. Пяти экспертам предложены для оценки на принадлежность к множеству «мало эффективных» госкорпораций по выше названному признаку х2. Результаты опроса приведены в таблице 2. Последняя строка таблицы содержит значения ![]() , рассчитанные по формуле (1). Указанный способ определения
, рассчитанные по формуле (1). Указанный способ определения ![]() достаточно прост, но обладает известной грубостью оценки.
достаточно прост, но обладает известной грубостью оценки.
Таблица 2
Исходные данные и результаты статистического расчета функции принадлежности
|
х2 |
500 |
1000 |
1500 |
2000 |
2500 |
3000 |
|
n1 |
5 |
4 |
3 |
2 |
1 |
0 |
|
|
1 |
0,8 |
0,6 |
0,4 |
0,2 |
0 |
Значения переменной х2 в таблице 2 задавались равномерно с целью более точно представить весь диапазон изменения выбранной переменной. Реально наблюдаемые значения (см. табл. 1) «не попадают» в выбранные ЛПР, и возникает задача аппроксимации ФП во всех точках признака. Кроме того, данные, анализируемые экспертами, «не привязаны» к конкретным ГК.
В ряде случаев предпочтительной представляется методика работы с несколькими экспертами.
Каждому из N экспертов предъявляется набор значений критериальной переменной:
Х = ![]() (2)
(2)
и предлагается дать численную оценку ![]() . В данной итерационной процедуре реализуется элемент обучения экспертов: они имеют возможность познакомиться с мнением других экспертов и на этом основании пересмотреть свое мнение. В результате опроса получаем таблицу вида 3. Здесь j – номер эксперта. Шкала оценок у экспертов может быть различной (двухбалльной: принадлежит – не принадлежит; пятибалльной, десятибалльной и др.) в зависимости от опыта и знаний эксперта. В этом случае необходимо предусмотреть обработку данных таблицы 3, сводящую все высказывания к единой системе измерений, потому что, например, оценка 4 в десятибалльной и пятибалльной системах имеет разное значение. Заблаговременно устанавливать шкалу не рекомендуется, чтобы обеспечить свободное изъявление мнений экспертами (в рамках их компетенций).
. В данной итерационной процедуре реализуется элемент обучения экспертов: они имеют возможность познакомиться с мнением других экспертов и на этом основании пересмотреть свое мнение. В результате опроса получаем таблицу вида 3. Здесь j – номер эксперта. Шкала оценок у экспертов может быть различной (двухбалльной: принадлежит – не принадлежит; пятибалльной, десятибалльной и др.) в зависимости от опыта и знаний эксперта. В этом случае необходимо предусмотреть обработку данных таблицы 3, сводящую все высказывания к единой системе измерений, потому что, например, оценка 4 в десятибалльной и пятибалльной системах имеет разное значение. Заблаговременно устанавливать шкалу не рекомендуется, чтобы обеспечить свободное изъявление мнений экспертами (в рамках их компетенций).
Таблица 3
Результаты опроса n экспертов по N сравниваемым ситуациям
|
j |
х1 |
х2 |
. . . . . . |
хN |
|
1 |
a11 |
a12 |
. . . . . . |
a1N |
|
. . . |
. . . |
. . . |
. . . . . . |
. . . . |
|
N |
an1 |
an2 |
. . . . . . |
anN |
В редких случаях, когда привлечение группы экспертов по объективным причинам не представляется возможным, целесообразным является использования метода парных сравнений. Суть данного метода в том, что единственный эксперт выносит суждение отдельно по каждой паре ситуаций. Данную процедуру можно сравнить с проведением ![]() независимых экспериментов, число которых определяется числом независимых элементов матрицы размерности N х N) [10]. Первым шагом этого процесса является численная оценка лингвистических высказываний, для чего эксперт заполняет таблицу, определяя качественные соотношения между вариантами, с последующим присвоением им «цены». [5].
независимых экспериментов, число которых определяется числом независимых элементов матрицы размерности N х N) [10]. Первым шагом этого процесса является численная оценка лингвистических высказываний, для чего эксперт заполняет таблицу, определяя качественные соотношения между вариантами, с последующим присвоением им «цены». [5].
Таблица 4
Численная оценка лингвистических высказываний
|
№№ |
Смысловое отношение |
Цена mij |
|
1 |
хi примерно соответствует хj |
1 |
|
2 |
Важность хi немного выше хj |
3 |
|
3 |
Важность хi выше хj |
5 |
|
4 |
Важность хi много выше хj |
7 |
В случае необходимости эксперт использует и другие значения «цены» важности, они будут промежуточными, например 2, 4, 6. Заполнение таблицы 4 осуществляется на основе знаний, интуиции и опыта конкретного эксперта. Составление таблицы парных сравнений объектов, в данном случае это таблица 5, основано на следующем определении: mii º 1, mji = 1/ mij . Целесообразно проиллюстрировать указанную процедуру следующим примером. Примем N = 6 и допустим, что с учетом этого эксперт сформулировал матрицу, характеризующую высказывания эксперта, идентифицирующего «мало эффективную» госкорпорацию. На пересечении первой строки и четвертого столбца m14 = 5. Экспертная оценка будет такая: «значение ситуации х1 выше значения ситуации х4». Далее, m23 = 3 значит следующее: «значение х2 немного выше значения х3». Единицы на главной диагонали матрицы означают, что она отражает отношения признака к себе. Часть матрицы под главной диагональю взаимна части, расположенной над нею. Ситуация с номером j относится к ситуации с номером i в обратном отношении, чем i к j.
Таблица 5
Матрица парных сравнений объектов, характеризующих «мало эффективную» госкорпорацию
|
|
х1 |
х2 |
х3 |
х4 |
х5 |
х6 |
|
х1 |
1 |
2 |
4 |
5 |
6 |
7 |
|
х2 |
1/2 |
1 |
3 |
4 |
5 |
6 |
|
х3 |
1/4 |
1/3 |
1 |
2 |
4 |
5 |
|
х4 |
1/5 |
1/4 |
1/2 |
1 |
2 |
3 |
|
х5 |
1/6 |
1/5 |
1/4 |
1/2 |
1 |
2 |
|
х6 |
1/7 |
1/6 |
1/5 |
1/3 |
1/2 |
1 |
Далее для каждого столбца матрицы найдем относительные значения важности ситуаций:
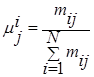 . (3)
. (3)
В результате расчетов получим следующую таблицу ![]() (табл. 6).
(табл. 6).
Таблица 6
Промежуточные результаты расчетов
|
|
х1 |
х2 |
х3 |
х4 |
х5 |
х6 |
|
х1 |
0,442 |
0,051 |
0,447 |
0,389 |
0,324 |
0,292 |
|
х2 |
0,221 |
0,253 |
0,335 |
0,312 |
0,270 |
0,250 |
|
х3 |
0,111 |
0,084 |
0,112 |
0,156 |
0,216 |
0,208 |
|
х4 |
0,088 |
0,063 |
0,056 |
0,078 |
0,108 |
0,167 |
|
х5 |
0,073 |
0,051 |
0,028 |
0,039 |
0,054 |
0,040 |
|
х6 |
0,063 |
0,042 |
0,022 |
0,026 |
0,027 |
0,020 |
Степени относительной важности ситуаций друг к другу, выраженные с разных точек зрения характеризует каждый столбец. Эти степени отличаются друг от друга от столбца к столбцу, что указывает на ошибочные высказывания в экспертном опросе. Для получения более надежных характеристик степеней важности ситуаций их значение следует усреднить:
![]() {0,400; 0,273; 0,148; 0,093; 0,048; 0,033}. (4)
{0,400; 0,273; 0,148; 0,093; 0,048; 0,033}. (4)
Полученное соотношение еще не может считаться функцией принадлежности нечеткого множества «мало эффективных» ГК, т.к. отражает лишь относительные веса принадлежности. Учитывая, что данное понятие имеет наиболее типичного представителя – госкорпорацию с х2 = 500, следует все полученные значения ![]() (Х) разделить на 0,4. Тогда соответствующая госкорпорация будет иметь
(Х) разделить на 0,4. Тогда соответствующая госкорпорация будет иметь ![]() (500) = 1. Окончательно получим:
(500) = 1. Окончательно получим:
![]() . (5)
. (5)
Примечание: поскольку числовые данные в таблице 6 и соотношение (4) являются промежуточными, они даны с точностью до трех знаков после запятой (вместо двух, как в (5)).
Смысл опосредованного определения сравнительной информативности параметров (иначе функции принадлежности) заключается в следующем. Решается некоторая конкретная задача: классификация объектов, строится регрессионная зависимость, определяется мера сравнения и т.д. Результат решения проявляет наиболее информативные для этой задачи ситуации, признаки и позволяет дать численную оценку степеней их информативности (значений функции принадлежности).
Результаты исследования. Применение вышеприведенных методов позволило оценить эффективность функционирования рассмотренных госкорпораций с отнесением к определенному классу. Однако при этом следует:
- различать абсолютную и относительную эффективность госкорпораций;
- ФП строить не относительно признаков, а относительно собственно наблюдаемых корпораций.
Абсолютная эффективность определяется «извне» посредством задания эталонных значений ключевых (критериальных) показателей и сравнения с ними существующих. Например, пусть различаются два класса госкорпораций: эффективные и неэффективные, а оценка госкорпораций ведется на основе признака х1 и правительством задано пороговое значение х1п = 10000 тыс. рублей. Тогда в соответствие с табл. 1 к эффективным госкорпорациям следует отнести только корпорацию ОАК, остальные не достигают установленного предела и относятся к неэффективным.
Функция принадлежности μЭ1(Вi) строилась по переменной x1, а μЭ2(Вi) по переменной x2.Анализ соотношений (9) и (10) показывает, что выбор критерия оценки существенно влияет на ее результат. Так, например, РОСАТОМ в первом случае является менее всего эффективным в выбранной группе госкорпораций, а во втором случае показывает пример наивысшей эффективности.
Очевидно, что, попав во вторую группу, три корпорации не равнозначны по степени неэффективности и требуется оценить это различие. Удобно выполнить это введя степень принадлежности μЭ(Вi) корпорации Вi к классу Э эффективных корпораций. В нашем случае это осуществим с помощью следующей формулы:
μЭ(Вi) = х1(Вi)/х1п , если х1(Вi) ≤ х1п и μЭ(Вi) = 1, если х1(Вi) ≥ х1п (6)
Разделив в (6) соответствующие значения ключевого показателя на пороговое значение, мы получаем долю выполнения установленного требования. В нашем случае согласно (6) получим функцию принадлежности:
μЭ(Вi) = (0,025/А; 0,043/Н; 0,90/Т; 1,0/О) (7)
Под чертой указаны госкорпорации, над чертой соответствующие значения функции принадлежности. Анализ (6) позволяет заключить, что госкорпорация РОСТЕХ приблизилась к заданному эталону, а РОСАТОМ и РОСНАНО находятся только в начале пути.
Определение относительной эффективности госкорпораций опирается на сравнение между собой существующих показателей госкорпораций. Оценка значений функции принадлежности в этом случае ведется по формуле:
μЭ(Вi) = (xi - min xi)/(max xi - min xi), (8)
где xi любая из исследуемых переменных. Это процедура масштабирования переменных. Она переводит произвольный промежуток изменения переменной в отрезок от 0 до 1. Минимальное значение исследуемого ряда данных соответствует 0, максимальное - 1. То есть в нашей постановке (приведенном определении относительной эффективности) значение функции принадлежности объекта с худшим показателем приравнивается нулю, а с максимальным - 1.
Построим функции принадлежности относительной эффективности по переменным табл. 1. Получим:
μЭ1(Вi) = (0,00/А; 0,01/Н; 0,40/Т; 1,0/О) (9)
μЭ2(Вi) = (0,00/Н; 0,49/О; 0,71/Т; 1,0/А) (10)
Функция принадлежности μЭ1(Вi) строилась по переменной x1, а μЭ2(Вi) по переменной x2.Анализ соотношений (9) и (10) показывает, что выбор критерия оценки существенно влияет на ее результат. Так, например, РОСАТОМ в первом случае является менее всего эффективным в выбранной группе госкорпораций, а во втором случае показывает пример наивысшей эффективности.
Второй подход к расчету функций принадлежности состоит в присвоении госкорпорации с наилучшими показателями значения 1, а для остальных оно рассчитывается как доля от этого значения. В этом случае получим:
μЭ1(Вi) = (0,01/А; 0,02/Н; 0,40/Т; 1,0/О) (11)
μЭ2(Вi) = (0,32/Н; 0,65/О; 0,80/Т; 1,0/А) (12)
Очевидно, что выводы по отдельным критериям не являются исчерпывающими. Нужны обобщающие характеристики. Здесь можно реализовать два подхода:
- сформировать на основе операций над нечеткими множествами более сложное определение эффективности;
- построить многомерную функцию принадлежности.
Формирование нового определения эффективности основывается на нескольких логических установках, задаваемых экспертом. Проведем это обобщение для случая двухкритериальных переменных.
В первом случае, если эксперт считает, что для оценки эффективности хозяйствующего субъекта достаточно учитывать или первый показатель, или второй (логическая сумма), то имеем объединение нечетких множеств и функция принадлежности рассчитывается по формуле:
μЭ(Вi) = (μЭ1(Вi) + μЭ2(Вi))/maxi (μЭ1(Вi) + μЭ2(Вi)) (13)
Используя (11) и (12), и правило (13), получим для объединения нечетких множеств «госкорпорация эффективная по доходу» и «госкорпорация эффективная по инвестициям»:
μЭо(Вi) = (0,21/Н; 0,61/А; 0,73/Т; 1,0/О) (14)
Во втором случае, если эксперт считает, что для оценки эффективности хозяйствующего субъекта, следует учитывать и первый показатель, и второй одновременно (логическое произведение), то имеем пересечение нечетких множеств и функция принадлежности рассчитывается по формуле:
μЭ(Вi) = (μЭ1(Вi) * μЭ2(Вi ))/maxi (μЭ1(Вi) * μЭ2(Вi)) (15)
Ниже по (11) и (12), и правилу (15), получена функция принадлежности для пересечения нечетких множеств «госкорпорация эффективная по доходу» и «госкорпорация эффективная по инвестициям»:
μЭп(Вi) = (0,01/Н; 0,02/А; 0,49/Т; 1,0/О) (16)
Проанализируем (14) и (16). Обе оценки дают одинаковое распределение исследуемых госкорпораций по эффективности (чего не наблюдалось при частной оценки на основе одного критериального показателя): эффективность РОСНАНО низшая, самой эффективной является ОАК. Оценки по (16) более жесткие, чем по (14) и это соответствует принятой логике рассуждений: удовлетворить и требованию 1, и требованию 2 одновременно сложнее, чем соответствовать или требованию 1, или требованию 2.
Выводы
1. Противоречие между статистическими и интуитивными (экспертными) методами анализа сложных ситуаций предлагается решить сочетанным использованием в допустимых пределах численных и логико-лингвистических приемов анализа данных. Это выражается во включение в процедуру построения ФП механизмов обучения экспертов, многократного экспертного мнения (метод парных сравнений), в переходе к зависимостям ФП не от признаков хi, а от хозяйствующих субъектов Bi.
2. Введено различие в понимание эффективности хозяйствующего субъекта. Снижение абсолютных показателей деятельности может быть вызвано изменениями среды погружения предприятия (экономический кризис), но если его сравнительное положение на рынке не ухудшается, то признается сохранение (повышение) относительной эффективности.
Публикация подготовлена в рамках поддержанного РГНФ научного проекта №14-02-00293.
Рецензенты:
Гриненко С.В., д.э.н., профессор, заведующий кафедрой инноватики и экономического проектирования ФГАОУ ВПО «Южный федеральный университет», г. Таганрог;
Макареня Т.А., д.э.н., профессор, заведующий кафедрой инженерной экономики ФГАОУ ВПО «Южный федеральный университет», г. Таганрог.
Библиографическая ссылка
Бабикова А.В., Лябах Н.Н., Федотова А.Ю., Ханина А.В., Шевченко И.К. ПРИМЕНЕНИЕ ТЕОРИИ НЕЧЕТКИХ МНОЖЕСТВ ДЛЯ ОЦЕНКИ ЭФФЕКТИВНОСТИ ФУНКЦИОНИРОВАНИЯ ГОСУДАРСТВЕННЫХ КОРПОРАЦИЙ // Современные проблемы науки и образования. – 2014. – № 6. ;URL: https://science-education.ru/ru/article/view?id=15581 (дата обращения: 19.04.2024).



