Слоистые магнитострикционно-пьезоэлектрические (МП) структуры интересны тем, что в них, в результате механического взаимодействия магнитострикционной и пьезоэлектрической компонент, возникают эффекты, которые отсутствуют по отдельности и в магнитострикционной и пьезоэлектрической фазах. Магнитоэлектрический (МЭ) эффект является одним из таких эффектов, который заключается в возникновении напряжения на обкладках конденсатора, диэлектриком которого является МП композит, при помещении его в магнитное поле. Двухслойные МП-структуры обладают определенными преимуществами по сравнению с объемными композитами [3]. В таких структурах величина МЭ-эффекта, как правило, больше, чем в объемных композитах. Это позволяет рассматривать слоистые композиты как перспективные материалы для создания устройств на основе МЭ-эффекта.
Теория МЭ-эффекта в таких структурах, развитая в работах [4‑6] и [1; 8; 11], основана на совместном решении уравнений эластодинамики и электростатики для магнитострикционной и пьезоэлектрической фаз с учетом условий на границе раздела. При этом учет клеевого соединения на границе раздела учитывался формально либо введением коэффициента связи между слоями [4-6] и [8], либо предполагалось, что связь идеальная и смещения пьезоэлектрической и магнитострикционной фаз одинаковы и не зависят по толщине слоя [1; 11]. Теория МЭ-эффекта в двухслойных структурах с учетом неоднородности смещений феррита и пьезоэлектрика по толщине слоев была построена в работе [7; 9], однако в этой работе не учитывалась клеевая прослойка, и связь между ферритом и пьезоэлектриком предполагалась идеальной. Недавно в работах [2; 10] была построена теория МЭ-эффекта в слоистых МП-структурах с учетом клеевого соединения магнитострикционной и пьезоэлектрической компонент. Однако в этих работах не было представлено пространственное распределение смещений и влияние толщины клея на величину смещений в магнитострикционной и пьезоэлектрической фазе.
В данной работе на основе совместного решения уравнений эластодинамики и электростатики получены выражения для зависимости амплитуды смещений с учетом клеевой прослойки. Построены теоретические зависимости смещений в магнитострикционной и пьезоэлектрической фазе по толщине образца при разных значениях толщины клея между слоями. Рассмотрено влияние клеевой прослойки на величину МЭ-эффекта в двухслойной МП-структуре.
Модель
В качестве модели рассмотрим структуру, представляющую собой клеевое соединение феррита и пьезоэлектрика в форме прямоугольной пластинки (рис. 1). Будем считать, что длина пластинки L много больше ее ширины W, в то время как толщину магнетика ![]() пьезоэлектрика
пьезоэлектрика ![]() и клея
и клея ![]() будем считать конечной величиной. Выберем систему координат таким образом, чтобы начало совпадало с границей раздела «клей – пьезоэлектрик», а ось Z направим вертикально вверх, перпендикулярно границе раздела.
будем считать конечной величиной. Выберем систему координат таким образом, чтобы начало совпадало с границей раздела «клей – пьезоэлектрик», а ось Z направим вертикально вверх, перпендикулярно границе раздела.
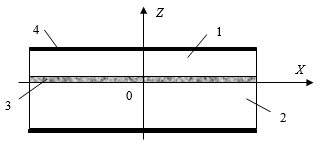
Рис. 1. Схематичное изображение структуры:
1 - магнитострикционный слой, 2 - пьезоэлектрический слой, 3 - клеевой слой, 4 - электроды
Пьезоэлектрический слой предварительно поляризован перпендикулярно плоскости контактов (ось Z). Ограничимся рассмотрением продольного эффекта. В этом случае магнитные поля (подмагничивающее ![]() и переменное
и переменное ![]() ) совпадают с направлением вектора поляризации.
) совпадают с направлением вектора поляризации.
Полагая пластинку узкой, в первом приближении можно считать, что вдоль оси Y смещения будут однородными, и отличными от нуля компонентами будут только компоненты напряжений ![]() и
и ![]() . Уравнение движения для x–проекции вектора смещения среды
. Уравнение движения для x–проекции вектора смещения среды ![]() запишем в виде:
запишем в виде:
![]() , (1)
, (1)
где индекс α равен соответственно m для магнитострикционного, p для пьезоэлектрического и G для клеевого слоя, ![]() – плотность феррита, пьезоэлектрика или клея соответственно,
– плотность феррита, пьезоэлектрика или клея соответственно, ![]() – тензор напряжений.
– тензор напряжений.
Уравнения для тензора деформаций ![]() для магнитострикционной, клеевой и пьезоэлектрической фазы имеют следующий вид:
для магнитострикционной, клеевой и пьезоэлектрической фазы имеют следующий вид:
![]() , (2)
, (2)
![]() , (3)
, (3)
![]() , (4)
, (4)
![]() , (5)
, (5)
![]() , (6)
, (6)
![]() , (7)
, (7)
![]() . (8)
. (8)
Здесь ![]() – пьезомагнитный тензор,
– пьезомагнитный тензор, ![]() – пьезоэлектрический тензор,
– пьезоэлектрический тензор, ![]() – тензор диэлектрической проницаемости пьезоэлектрика,
– тензор диэлектрической проницаемости пьезоэлектрика, ![]() – модули Юнга и модули сдвига,
– модули Юнга и модули сдвига, ![]() и
и ![]() – z-проекция вектора напряженности электрического и магнитного полей в пьезоэлектрике и магнетике соответственно.
– z-проекция вектора напряженности электрического и магнитного полей в пьезоэлектрике и магнетике соответственно.
Так как имеется неоднородность вдоль оси Z, решение уравнение для вектора смещения среды представим в виде плоских волн, амплитуда которых изменяется по толщине образца
![]() , (9)
, (9)
где ![]() и
и ![]() – постоянные интегрирования, ω – угловая частота, k – волновое число,
– постоянные интегрирования, ω – угловая частота, k – волновое число, ![]() – некоторая функция.
– некоторая функция.
Условия механического равновесия на свободных боковых поверхностях образца в точках ![]() дают следующие граничные условия:
дают следующие граничные условия:
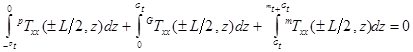 . (10)
. (10)
Используя эти граничные условия и уравнение (9), для смещения магнитострикционной и пьезоэлектрической среды получим следующие выражения:
![]() , (11)
, (11)
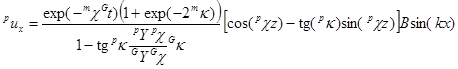 , (12)
, (12)
где
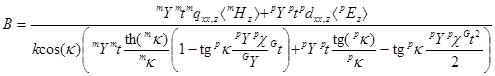 ;
; ![]() и
и ![]() безразмерные параметры;
безразмерные параметры; 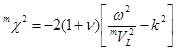 ,
, 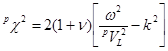 ,
, 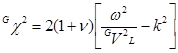 ;
; ![]() ,
, ![]() – скорости продольных волн,
– скорости продольных волн, ![]() – коэффициент Пуассона. Как видно из уравнений (11) и (12), решения представляют собой плоские волны, амплитуда которых изменяется по толщине образца. Эта зависимость имеет нелинейный характер и в общем случае зависит не только от частоты колебаний, но и от толщины клея. Легко показать, что в случае низких частот, когда безразмерные параметры
– коэффициент Пуассона. Как видно из уравнений (11) и (12), решения представляют собой плоские волны, амплитуда которых изменяется по толщине образца. Эта зависимость имеет нелинейный характер и в общем случае зависит не только от частоты колебаний, но и от толщины клея. Легко показать, что в случае низких частот, когда безразмерные параметры ![]() меньше единицы, амплитуда перестает зависеть по толщине образца.
меньше единицы, амплитуда перестает зависеть по толщине образца.
На рис. 2 и 3 представлены рассчитанные по уравнениям (11) и (12) теоретические зависимости смещений магнитострикционной и пьезоэлектрической фазы для двухслойной структуры никель – цирконат-титанат свинца (Ni‑PZT), приклеенной эпоксидным клеем, толщина которой меняется.
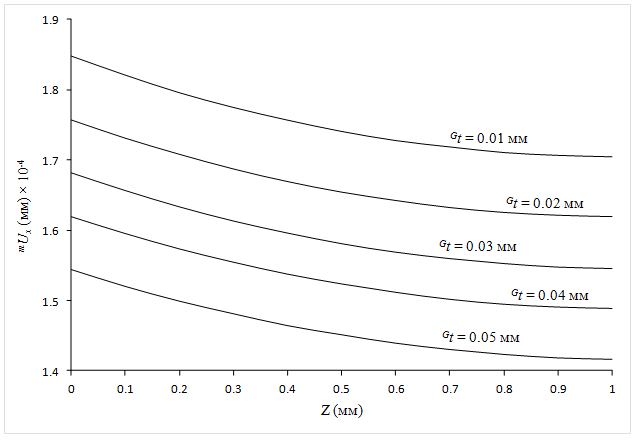
Рис. 2. Зависимость смещений среды магнитострикционной фазы по толщине образца. Толщина магнитострикционной фазы 1 мм. Толщина клея меняется от 0.01 до 0.05 мм. Частота переменного магнитного поля f = 300 кГц
При расчетах использовались следующие параметры: для никеля – ![]() ,
, ![]() ,
, ![]() ; для ЦТС –
; для ЦТС – ![]() ,
, ![]() ,
, ![]() ,
, ![]() ; для клея –
; для клея – ![]() ,
, ![]() . Напряженность переменного магнитного поля при расчетах принималась равной H=100 Э.
. Напряженность переменного магнитного поля при расчетах принималась равной H=100 Э.
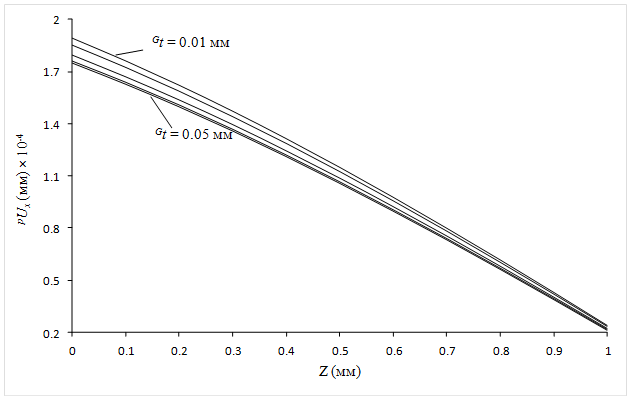
Рис. 3. Зависимость смещений среды пьезоэлектрической фазы по толщине образца. Толщина пьезоэлектрической фазы 1 мм. Толщина клея меняется от 0.01 до 0.05 мм. Частота переменного магнитного поля f = 300 кГц
Как следует из рис. 2 и 3, амплитуда колебаний магнитострикционной фазы практически не изменяется по толщине слоя магнетика. Это объясняется тем, что переменное магнитное поле возбуждает колебания магнитострикционной среды одновременно по всей толщине слоя магнетика. В пьезоэлектрическом слое колебания возбуждаются посредством сдвиговых деформаций через границу раздела «клей – пьезоэлектрик». Это приводит к тому, что амплитуда колебаний пьезоэлектрического слоя значительно уменьшается с глубиной. Из рисунков также следует, что величина смещений магнитострикционной и пьезоэлектрической фазы уменьшается с увеличением толщины клея.
Магнитоэлектрический коэффициент по напряжению
Магнитоэлектрический коэффициент по напряжению определяется как отношение среднего значения напряженности электрического поля в структуре к среднему значению напряженности внешнего магнитного поля, ее вызвавшей т.е.:
![]() , (13)
, (13)
где ![]() – среднее значение напряженности электрического поля в структуре, U ‑ возникающая разность потенциалов между электродами.
– среднее значение напряженности электрического поля в структуре, U ‑ возникающая разность потенциалов между электродами.
Подставляя в уравнение (8) тензор напряжения из (6), с использованием условия разомкнутой цепи для МЭкоэффициента по напряжению, при продольном эффекте получим следующее выражение:
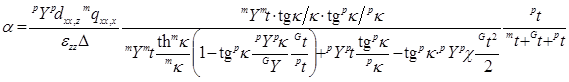 , (14)
, (14)
где
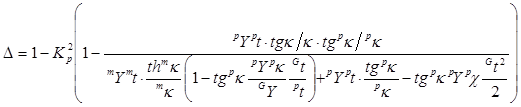 ,
,
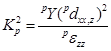 ‑ квадрат коэффициента электромеханической связи.
‑ квадрат коэффициента электромеханической связи.
Как следует из выражения (14), частотная зависимость МЭ-коэффициента по напряжению в одинаковой мере зависит от параметров магнитострикционного, клеевого и пьезоэлектрического слоев. Легко показать, что в случае, когда толщина клея стремится к нулю, выражение для МЭ-коэффициента переходит в выражение для МЭ-коэффициента по напряжению для случая идеальной связи, полученное ранее в работе [8; 9]. Таким образом, представленное уравнением (14) выражение для МЭ-коэффициента по напряжению является более общим, чем выражения, полученные ранее.
Вывод. Неоднородность структуры, связанная с наличием клеевой прослойки между ферритом и пьезоэлектриком, приводит к неоднородному распределению амплитуды смещений по толщине образца. Величина смещений магнитострикционной и пьезоэлектрической фазы уменьшается с увеличением толщины клея. Учет межслоевой клеевой прослойки в двухслойной МП-структуре приводит к изменению величины МЭ-коэффициента по напряжению. Полученное соотношение в предельном случае, когда толщина клея стремится к нулю, переходит в соотношение, полученное ранее для случая идеальной связи.
Рецензенты:
Филиппов Д.А., д.ф.-м.н., профессор, Новгородский государственный университет, заведующий кафедрой технологии машиностроения, г. Великий Новгород;
Швецов И.В., д.т.н., профессор, Новгородский государственный университет, заведующий кафедрой промышленной теплоэнергетики, г. Великий Новгород.
Библиографическая ссылка
Галичян Т.А. ВЛИЯНИЕ КЛЕЕВОЙ ПРОСЛОЙКИ НА МАГНИТОЭЛЕКТРИЧЕСКИЙ ЭФФЕКТ В МАГНИТОСТРИКЦИОННО-ПЬЕЗОЭЛЕКТРИЧЕСКИХ СТРУКТУРАХ // Современные проблемы науки и образования. – 2014. – № 6. ;URL: https://science-education.ru/ru/article/view?id=15436 (дата обращения: 26.04.2024).



