Расчет многих электротехнических устройств предполагает необходимость учета поверхностного эффекта в массивных проводниках в установившемся режиме при периодических токах. В этих устройствах массивными проводниками могут быть обмотки электрических машин, трансформаторов и устройств индукционного нагрева, а также шинопроводы электропитания разнообразных электроэнергетических установок.
Учет поверхностного эффекта существенно упрощается с использованием таких эквивалентных параметров массивных проводников как глубина проникновения электромагнитного поля в проводник (толщина скин-слоя) и его температура, сопротивление и внутренняя индуктивность [1–6].
Поэтому расчет эквивалентных параметров массивных проводников с учетом поверхностного эффекта и нагрева в установившемся режиме при периодических токах представляется актуальной задачей.
Цель данной работы заключается в получении аналитических формул для инженерного расчета эквивалентных параметров массивных проводников с учетом их нагрева в установившемся режиме.
Допущения
Для получения расчетных формул сделаем следующие допущения.
1. Вся толща проводника характеризуется постоянными значениями температуры 
(°С), магнитной проницаемости 
(Гн/м) и удельной проводимости 
(1/Ом·м), причем [6]:
, (1)
где 
– удельная проводимость при температуре окружающей среды 
(°С);
– постоянный температурный коэффициент (1/°С).
2. Растекание тока вдоль проводника (краевой эффект) и влияние соседних проводников с токами (эффект близости) учитывать не будем, считая при этом, что площадь поперечного сечения проводника S0 (м2) и его внешний периметр 
(м) постоянны.
3. Коэффициент теплообмена поверхности проводника с окружающей средой 
[Вт/(м2 °С)] неизменен и определяется условиями теплоотвода благодаря конвекции и теплоизлучению [6].
4. Размеры массивных проводников и радиусы кривизны их поверхности существенно превосходят глубину проникновения в них электромагнитного поля, изменяющегося c частотой f, поэтому будем исходить из представления о плоской одномерной электромагнитной волне, проникающей в проводящее полупространство перпендикулярно его поверхности и полностью затухающей в его теле [1, 5].
Методика расчета
В самом общем случае периодический ток в проводнике может быть представлен так [3]:
(2)
при активной потребляемой мощности
, (3)
где R0 и Rk – активные сопротивления массивного проводника постоянной составляющей I0 и k-гармонике тока соответственно;
Ik – действующее значение k-гармоники тока;
n – число учитываемых гармоник.
При этом для инженерных вычислений может быть использован метод эквивалентных синусоид [4], когда ток и напряжение, записанные в виде:
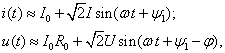(4)
отражают результирующее энергетическое воздействие тока (2) на проводник, характеризуемое активной мощностью:
, (5)
и следующими действующими значениями эквивалентных синусоид:
; 
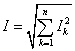, (6)
где R и L – активное сопротивление и внутренняя индуктивность проводника эквивалентной синусоиде тока;
L0 – индуктивность внешнего магнитного поля;
– угловая частота эквивалентной синусоиды (первой гармоники) тока.
Для метода эквивалентных синусоид были бы удобны аналитические выражения для эквивалентных параметров массивных проводников R0, R и L, учитывающие поверхностный эффект и нагрев проводника, а также гармонический состав тока. Для этого подобно синусоидальному режиму [1, 2, 5] запишем для несинусоидального тока (2):
; 
; 
, (7)
где 
– длина проводника;
ΔR и ΔL – эквивалентная толщина скин-слоя для эквивалентной синусоиды тока и для её магнитной энергии соответственно.
При этом для первой гармоники тока с угловой частотой 
активное сопротивление и внутренняя индуктивность согласно (7) и [1, 2, 5] составят:
; 
, (8)
где 
– эквивалентная глубина проникновения в проводник как проводящее полупространство первой гармоники тока.
Очевидно, при увеличении угловой частоты в k-раз эти величины для гармоник тока составят
; 
. (9)
Далее воспользуемся активной и реактивной мощностью для эквивалентной синусоиды тока
; 
, (10)
которые на основании (3, 5, 8, 9) представим так
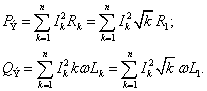(11)
С учетом выражений (6, 7, 8, 10, 11) имеем
; 
, (12)
где через N обозначен безразмерный параметр:
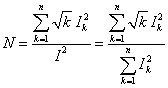. (13)
Из соотношения (13) нетрудно заметить, что 
, причем этот параметр тем больше, чем существеннее несинусоидальность тока. Величина N не зависит от начальных фаз гармоник тока, а определяется лишь их действующими значениями. При этом из выражений (12) следует, что чем заметнее несинусоидальность, тем меньше эквивалентная толщина скин-слоя для эквивалентной синусоиды тока ΔR и больше эквивалентная толщина скин-слоя для её магнитной энергии ΔL. Однако, как и для синусоидального тока выполняется известное равенство для проводящего полупространства [5]:
,
т.е. с увеличением несинусоидальности одинаково возрастают активное и индуктивное сопротивления массивного проводника.
Для определения температуры проводника θ воспользуемся уравнением теплового баланса [6]:
(14)
и соотношениями (1, 3, 5, 6, 7, 12, 13), на основании которых при коэффициенте теплообмена
(15)
получаем установившуюся температуру проводника
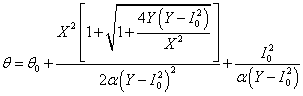(16)
при расчетных параметрах
; 
(17)
и эквивалентной глубине проникновения в проводник первой гармоники тока при температуре проводника, равной температуре окружающей среды :
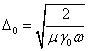. (18)
Результаты расчета
По формулам (1–18) для периодических токов с амплитудой 
(А) и периодом T проведены расчеты эквивалентных параметров массивного проводника из отожженной меди с параметрами [6, 7]: 
(Гн/м); 
(°С); 
(См/м); 
(1/°С); 
[Вт/(м2 °С)]; 
(м); 
(м); 
(м2); 
(Гц); 
(с); 
(1/с); 
(мм).
1. При переменном токе (рис. 1)
и N=1 результаты расчета приведены в табл. 1.
2. Для тока в виде однополярных прямоугольных периодических импульсов длительностью τ (рис. 2) при скважности
и постоянной составляющей
,
для действующих значений гармоник [3]
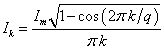
и 
результаты расчета приведены в табл. 2.
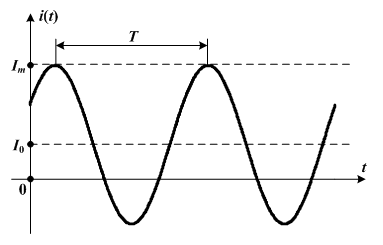
Рис. 1. Переменный ток: Im – амплитуда; I0 – постоянная составляющая; T – период
Таблица 1
Параметры массивного проводника из отожженной меди при переменном токе с амплитудой (А), при частоте (Гц) и N=1
|
|
– |
0 |
0,2 |
0,4 |
0,6 |
0,8 |
0,999 |
|
|
°С |
167 |
112 |
85 |
80 |
99 |
157 |
|
|
– |
0,612 |
0,717 |
0,783 |
0,796 |
0,746 |
0,630 |
|
|
мм |
11,95 |
11,04 |
10,56 |
10,48 |
10,82 |
11,77 |
|
|
мм |
5,97 |
5,52 |
5,28 |
5,24 |
5,41 |
5,88 |
|
R0 |
мкОм |
2,82 |
2,41 |
2,20 |
2,17 |
2,31 |
2,74 |
|
R |
мкОм |
5,90 |
5,45 |
5,21 |
5,17 |
5,34 |
5,81 |
|
L |
мкГн |
0,019 |
0,017 |
0,017 |
0,016 |
0,017 |
0,018 |
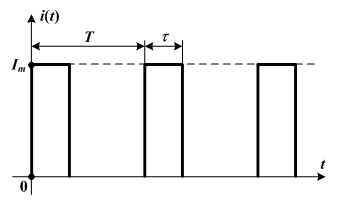
Рис. 2. Однополярные прямоугольные периодические импульсы тока: 
– длительность импульсов
Таблица 2
Параметры массивного проводника из отожженной меди при однополярных прямоугольных периодических импульсах тока с амплитудой (А) и при частоте (Гц)
|
|
– |
32 |
16 |
8 |
4 |
2 |
1,02 |
|
|
– |
0,031 |
0,063 |
0,125 |
0,250 |
0,500 |
0,980 |
|
N |
– |
3,429 |
2,542 |
1,919 |
1,511 |
1,334 |
4,205 |
|
|
°С |
45 |
57 |
75 |
103 |
149 |
186 |
|
|
– |
0,903 |
0,862 |
0,808 |
0,736 |
0,643 |
0,583 |
|
|
мм |
2,87 |
3,96 |
5,42 |
7,209 |
8,74 |
2,91 |
|
|
мм |
16,87 |
12,80 |
9,98 |
8,231 |
7,77 |
25,73 |
|
R0 |
мкОм |
1,91 |
2,00 |
2,14 |
2,34 |
2,68 |
2,96 |
|
R |
мкОм |
16,65 |
12,63 |
9,85 |
8,12 |
7,67 |
25,40 |
|
L |
мкГн |
0,053 |
0,040 |
0,031 |
0,026 |
0,024 |
0,081 |
Заключение
1. Предложена методика для аналитического определения эквивалентных параметров массивных проводников с учетом поверхностного эффекта и нагрева в установившемся режиме при периодических токах, которая может использоваться для инженерного расчета обмоток электрических машин, трансформаторов и устройств индукционного нагрева, а также шинопроводов электропитания разнообразных электроэнергетических установок.
2. Температура массивного проводника, эквивалентная толщина скин-слоя для эквивалентной синусоиды тока и для её магнитной энергии, сопротивление и внутренняя индуктивность зависят от удельной проводимости и магнитной проницаемости, частоты первой гармоники, постоянной составляющей и действующих значений гармоник тока, периметра и площади поперечного сечения, температурного коэффициента и теплообмена с окружающей средой.
3. Разработанная методика может использоваться для расчета эквивалентных параметров неферромагнитных и ферромагнитных массивных проводников при постоянной магнитной проницаемости и периодических токах любой формы, в том числе и синусоидальной.
Рецензенты:
Усов Ю.П., д.т.н., профессор кафедры ЭСиЭ ЭНИН ФГАОУ ВО НИ ТПУ, Национальный исследовательский Томский политехнический университет, г. Томск;
Канев Ф.Ю., д.ф.-м.н., ведущий научный сотрудник института оптики атмосферы им. В. Е. Зуева СО РАН, г. Томск.
Библиографическая ссылка
Носов Г.В. ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ МАССИВНЫХ ПРОВОДНИКОВ ПРИ ПЕРИОДИЧЕСКИХ ТОКАХ // Современные проблемы науки и образования. – 2014. – № 6. ;URL: https://science-education.ru/ru/article/view?id=15378 (дата обращения: 11.10.2024).