Как отмечено авторами в работе [6], работоспособность технологического оборудования обеспечивается рядом параметров механизма привода, основными из которых являются силовые параметры, которые должны обеспечивать передачу движения между звеньями механизмов с требуемыми кинематическими параметрами согласно заданным законам движения. Величины силовых факторов в зонах контакта звеньев зависят от особенностей структуры и условий дальнейшей эксплуатации механизма. Результатом силового взаимодействия звеньев механизмов являются силовые параметры, которые подразделяются на статические и динамические силы. Статические силовые факторы условно считаются постоянными величинами, а динамические силовые факторы изменяютcя пропорционально скорости движения звеньев содержащихся в структуре механизма.
Процесс модернизации и развития промышленного потенциала России показывает актуальность поиска новых структурных схем механизмов, позволяющих реализовывать сложные движения звеньев при минимально возможном числе подвижных соединений. Это дает возможность формировать привода технологического оборудования с требуемыми свойствами и показателями качества, что возможно только при правильном определении силовых параметров механизмов используемого вида. Перечисленным свойствам соответствуют механизмы с замкнутой системой тел качения (ЗСТК). Коллектив авторов проводит исследования параметров исполнительных механизмов технологического оборудования разработанного на базе механизмов с ЗСТК с диаметрами разной (эксцентриковые) [1-2, 6-9] или равной (соосные) [3-5, 10] величины. В ходе исследований
[1-10] установлено, что задача определения номинальных значений геометрических параметров механизмов с ЗСТК имеет решение только при двух направлениях ввода поправки, т. е. либо 
, либо 
.
Для механизмов с ЗСТК с диаметрами разной величины характерно наличие нескольких видов симметричных структурных схем механизмов (рис. 1). Наличие сепаратора в структуре механизмов с ЗСТК позволяет исключить контакт тел качения друг с другом, обеспечив между ними наличие зазора. Передача движения между звеньями в этом случае осуществляется посредством контакта тел качения с дорожками качения обоих колец. Механизмы данного вида относятся к фрикционным эпициклическим механизмам. В этом случае для обеспечения работоспособности механизмов с ЗСТК обладающих требуемыми свойствами и показателями качества необходимо сформировать достаточное по величине прижатие контактирующих поверхностей звеньев, что возможно только при правильном определении как статических, так в последующем и динамических силовых параметров.
В работе [6] авторами предложен алгоритм решения поставленной задачи на примере зоны тел качения с максимальными диаметрами. Однако, особенности геометрии и состава структуры каждого вида механизма с ЗСТК (рис. 1) не позволяют полностью применить полученный алгоритм для зоны тел качения с минимальными диаметрами.
Настоящее исследование проводится с целью дальнейшей разработки алгоритма расчета величин статических сил, действующих в точках контакта дорожек качения обоих колец с телами качения, расположенных в пределах зоны силового нагружения минимальных диаметров механизмов с ЗСТК. Полученный алгоритм обеспечивает учет обоих направлений ввода поправки в расчет номинальных величин геометрических параметров, а также наличия или отсутствия зазора между телами качения. Результаты выполненных исследований позволят обеспечить работоспособность приводов технологического оборудования на базе механизмов с ЗСТК с диаметрами разной величины для любого вида симметричной структурной схемы (рис. 1) обладающих требуемыми свойствами и показателями качества.
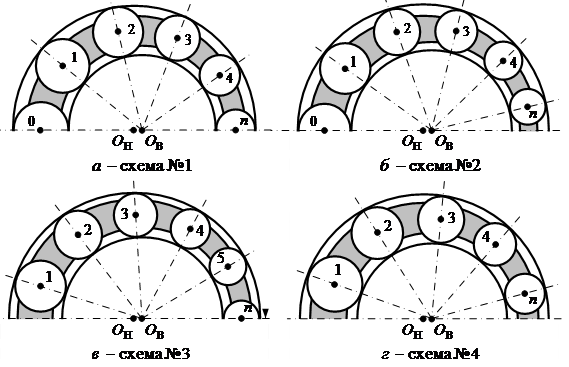
Рис. 1 Виды симметричных структурных схем механизмов с ЗСТК с диаметрами разной величины
Методы исследования, применяемые в настоящей работе, основаны на принципах силового анализа эпициклических фрикционных механизмов при использовании положений геометрии и тригонометрии.
В соответствии с вышеуказанной целью рассмотрим ход решения поставленной задачи на примере расчета величин статических сил при действии внешней радиальной силы на внутреннее кольцо механизма с ЗСТК. При этом учитываем оба направления ввода поправки в расчет номинальных величин геометрических параметров как при наличии зазора между телами качения, так и при отсутствии в структуре данного параметра для всех видов симметричных структурных схем (рис. 1). Составим расчетную модель (рис. 2) и примем следующие исходные условия и обозначения: все звенья являются абсолютно твердыми телами; 
, 
– дорожки качения внутреннего и наружного колец; RВ, RН, ОВ и
OН – радиусы и геометрические центры дорожек качения внутреннего и наружного колец;
e – эксцентриситет; S – сепаратор (водило); c – зазор между телами качения; rn, r(n-1), ri, n,
, i, 
, 
, 
и 
, 
, 
– радиусы, геометрические центра и точки контакта минимального, следующего и i-ого тел качения с дорожками качения внутреннего и наружного колец; bi и 
– углы положения i-ого тела качения; 
– угол клина, образованный дорожками качения колец; XВ OВ YВ – неподвижная система координат с центром в точке ОВ; Q – внешняя радиальная сила, действующая на внутреннее кольцо.
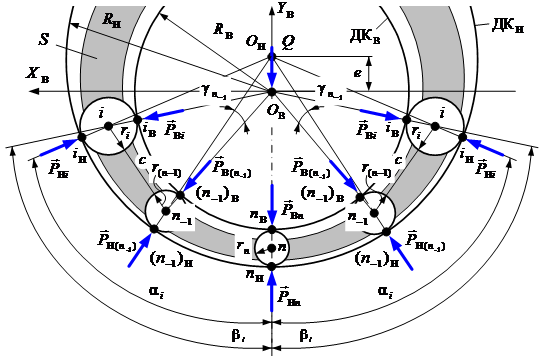
Рис. 2 Расчетная модель механизма с ЗСТК для зоны минимальных диаметров
Анализ расчетной модели (рис. 2) при рассматриваемых условиях показывает, при действии на внутреннее кольцо механизма с ЗСТК внешней радиальной силы Q минимальное тело качения находится под действием двух равных статических сил 
и 
, приложенных в точки и , которые соответствуют точкам контакта этого ролика с дорожками качения обоих колец. В тоже время i-ое тело качения находится под действием двух статических сил 
и 
, приложенных в точки 
и 
соответствующие точкам контакта этого ролика с дорожками качения внутреннего и наружного колец. Так как точки и не лежат на одной прямой, то силовые факторы не будут равны по величине, т. е. 
. Для определения величин силовых факторов, представим уравнение силового равновесия всех статических сил действующих в точках контакта дорожки качения внутреннего кольца с телами качения в зоне минимальных диаметров, в виде суммы проекций всех сил на ось Y в неподвижной системе координат XВ OВ YВ. В результате преобразования уравнения силового равновесия в соответствии с работой [1] будем иметь
(1)
где n – число тел качения механизма с ЗСТК в пределах половины зоны силового нагружения тел качения с минимальными диаметрами, соответствующей углу положения тел качения (bi) в пределах от 00 до 900.
В соответствие с работой [1] статические силы, приложенные в точки 
и 
, представим как
(2)
(3)
С учетом равенства (2), выражение (1) примет вид
(4)
здесь 
– геометрический параметр тел качения, определяемый по формуле
(5)
Проведя преобразование равенства (4), получим
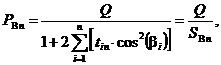(6)
где 
– геометрический параметр механизма с ЗСТК.
Выражение (6) позволит рассчитать значения статических сил и , приложенных в точки 
и 
соответствующие точкам контакта минимального тела качения с дорожками качения обоих колец принимающих одинаковые значения.
Подставив в формулу (2) равенство (6), получим
(7)
С учетом выражения (7) приведем формулу (3) к виду
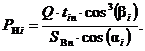(8)
Выражения (7) и (8) позволяют рассчитать статические силы, приложенные в точки и соответствующие точкам контакта i-ого тела качения с дорожками качения обоих колец, в пределах половины зоны силового нагружения тел качения с минимальными диаметрами. Геометрические параметры тел качения механизма с ЗСТК в выражениях (7) и (8) рассчитываются по формулам (5) и (6) соответственно.
Используя программный комплекс «Эксцентрик», по формулам (5)-(8) выполняем расчет величин статических сил, приложенных в точки контакта тел качения с дорожками качения обоих колец, расположенных в пределах половины зоны силового нагружения тел качения с минимальными диаметрами. Вычисления проводим для всех видов симметричных структурных схем механизмов рассматриваемого вида для обоих направлений ввода поправки в расчет номинальных величин геометрических параметров как при наличии зазора между телами качения, так и при отсутствии в структуре данного параметра. При расчетах считаем, что механизм с ЗСТК обладает основными геометрическими параметрами RН = 100 мм, RВ = 50 мм, е = 6 мм, с = 6 мм, а внешняя радиальная сила Q = 10000 Н. По полученным результатам выполняем синтез диаграмм статических сил (рис. 3).
Анализ диаграмм статических сил, действующих в точках контакта тел качения с минимальными диаметрами с дорожками качения внутреннего кольца (рис. 3, кривые 1в, 2в, 3в, 4в) и наружного кольца (рис. 3, кривые 1н, 2н, 3н, 4н) показывает на незначительное расхождение их величин пропорциональное изменению угла клина (gi). Совпадение значений сил для кривых 1в и 1н, а также 3в и 3н наблюдается только для минимального тела качения находящегося в зоне силового нагружения не зависимо от наличия или отсутствия зазора между телами качения. Отсутствие зазора между телами качения приводит к смещению кривых 2в и 2н, а также 3в и 3н вдоль оси радиусов тел качения в направлении роста значений этих параметров.
Особенности состава структуры каждого вида механизма с ЗСТК (рис. 1) с диаметрами разной величины и направление ввода поправки в расчет номинальных величин геометрических параметров для зоны минимальных диаметров также как и для зоны максимальных диаметров не оказывают влияния на вид кривых статических сил для каждой зоны в отдельности. Однако при сравнении обоих зон диаметров видим, что для зоны минимальных диаметров кривые статических сил имеют убывающий характер изменения, хотя в зоне максимальных диаметров данные кривые являются возрастающими [6].
В тоже время особенности состава сказываются на диапазонах величин статических сил. Так диапазон значений статических сил соответствующий кривым 1в и 1н объясняется наличием в структуре механизма на горизонтальной оси симметрии максимального и минимального тел качения и наибольшим числом тел качения в зоне силового нагружения.
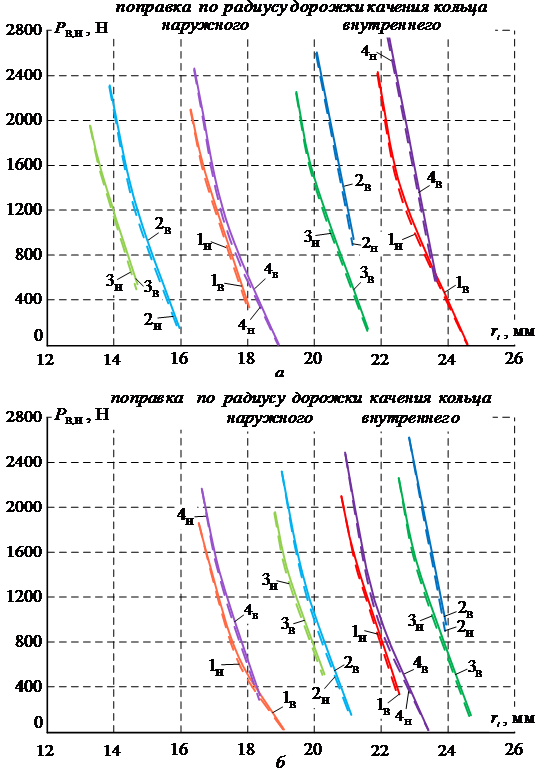
Рис. 3 Диаграммы статических сил для зоны минимальных диаметров
механизмов с ЗСТК: а – с зазором между телами качения, б – без зазора
При вводе поправки по радиусу дорожки качения наружного кольца кривым 2в и 2н (рис. 3) соответствует более широкий диапазон статических сил, сформированный в результате роста максимальных значений при уменьшении границы минимальных величин. Это является следствием отсутствия на горизонтальной оси симметрии минимального тела качения и снижением величин радиусов тел качения. Ввод поправки по радиусу дорожки качения внутреннего кольца для кривых 2в и 2н (рис. 3) соответствует более узкий диапазон статических сил, что объясняется снижением числа тел качения в зоне силового нагружения.
Более узкий диапазон значений статических сил соответствующий кривым 3в и 3н (рис. 3) по сравнению с кривыми 1в, 1н, 2в и 2н объясняется наличием в структуре механизма с ЗСТК на горизонтальной оси симметрии только минимального тела качения. Направление ввода поправки не оказывает влияния на число тел качения в зоне силового нагружения. Однако при вводе поправки по дорожке качения внутреннего кольца статические силы рассматриваемого вида принимаю большие значения.
Кривым 4в и 4н (рис. 3) соответствует наибольший диапазон статических сил, сформированный в результате отсутствия на горизонтальной оси симметрии и максимального и минимального тел качения. При вводе поправки по дорожке качения внутреннего кольца практически для всех видов симметричных структурных схем (рис. 1) статические силы рассматриваемого вида принимаю наибольшие значения, а при наличии зазора наблюдается снижение числа тел качения в зоне силового нагружения.
Заключение. В результате получены формулы для расчета величин статических сил, приложенных в точки контакта дорожек качения обоих колец с телами качения с минимальными диаметрами, расположенных в пределах зоны силового нагружения для любого вида симметричной структурной схемы механизмов с ЗСТК (рис. 1). Данные вычисления можно выполнять для обоих направлений ввода поправки в расчет номинальных величин геометрических параметров как при наличии зазора между телами качения, так и при отсутствии в структуре данного параметра. Установлен характер изменения и диапазон возможных значений статических сил данного вида. Это позволяет обеспечить работоспособность приводов технологического оборудования разработанных на базе механизмов с ЗСТК обладающих требуемыми свойствами и показателями качества.
Рецензенты:
Меновщиков В.А., д.т.н., профессор, профессор кафедры «Прикладная механика», ФГАОУ ВПО «Сибирский федеральный университет», г. Красноярск;
Еркаев Н.В., д.ф.-м.н.., профессор, профессор кафедры «Прикладная механика», ФГАОУ ВПО «Сибирский федеральный университет», г. Красноярск.
Библиографическая ссылка
Мерко М.А., Меснянкин М.В., Мерко И.С., Митяев А.Е., Колотов А.В., Кайзер Ю.Ф., Лысянников А.В., Лысянникова Н.Н. РАСПРЕДЕЛЕНИЕ СТАТИЧЕСКИХ СИЛ ПО ТОЧКАМ КОНТАКТА ЗВЕНЬЕВ МЕХАНИЗМОВ С ЗАМКНУТОЙ СИСТЕМОЙ ТЕЛ КАЧЕНИЯ В ЗОНЕ МИНИМАЛЬНЫХ ДИАМЕТРОВ // Современные проблемы науки и образования. – 2014. – № 6. ;URL: https://science-education.ru/ru/article/view?id=15346 (дата обращения: 19.04.2024).