Обработка большого объема экспериментальных данных требует, как правило, их классификации по существенным признакам. Одним из распространенных и эффективных алгоритмов классификации данных является методика кластерного анализа. В настоящей работе дано описание алгоритма и особенностей выполненной автором реализации функции построения кластерного дерева в среде программирования Mathematica 9.0.
В 1939 году американский психолог Роберт Трион в своих статьях, посвященных психометрике, и работах об индивидуальных различиях человека дал первоначальное описание основных методик кластерного анализа, определив главное назначение как разбиение множества исследуемых объектов и признаков на однородные группы – кластеры. Достоинство данного метода заключалось в том, что с его помощью можно проводить разбиение множества объектов по целому ряду признаков, а не только по одному параметру. Кластерный анализ позволяет изучать огромное множество данных, имеющих произвольную природу, не накладывая ограничений на изучаемые объекты.
Существует целый ряд пакетов прикладных программ, позволяющих провести кластерный анализ, а также отразить его результаты в виде кластерного дерева – дендрограммы. Однако для более точной классификации и построения таксономий объектов и последующего прогнозирования на основе дискриминантного анализа требуется использование нестандартных мер расстояния, что не предусмотрено в пакетах прикладных программ специализированного назначения. Помимо этого, построение кластерных деревьев для больших объемов данных стандартные процедуры кластеризации (реализованные, например, в расчетных средах Statistica 8.0, Язык программирования R, Matlab 6.5) зачастую неоптимально используют пространство рисунка, а получаемые с их помощью кластерные деревья порой сложно использовать для визуального определения принадлежности разных объектов кластерам.
В настоящей работе ставится и решается задача разработки алгоритма кластеризации большого объема данных на основе произвольной (определяемой пользователем) функции расстояния в пространстве кластеризуемых объектов. При этом предъявляются высокие требования к формату изображения кластерного дерева: при изображении дерева программа кластеризации должна оптимально использовать отведенное для рисунка место, то есть, количество узлов дерева на единицу площади рисунка должно быть приблизительно постоянным.
1. Алгоритм кластеризации данных большого объема и особенности его программной реализации
Напомним, что в математической статистике под кластером понимается объединение нескольких однородных элементов, которое может рассматриваться как самостоятельная единица, обладающая определенными свойствами. Всюду на протяжении настоящей работы мы будем исходить из следующего определения.
Определение. Пусть на множестве объектов X задана функция расстояния (метрика), то есть, рефлексивная и симметричная функция d:X×X →
. Элементы x, y множества X лежат в одном кластере при заданном уровне значимости p, если а) либо d(x,y) ≤ p; б) либо существует набор элементов 
множества X, такой, что 
и d(
) ≤ p для всех k=1,…,n-1.
Результатом работы алгоритма кластеризации является, в частности, изображение кластерного дерева, которое содержит информацию о виде кластеров для всех значений уровня значимости из диапазона от наименьшего из расстояний между элементами множества X до диаметра данного множества.
Существующие реализации алгоритмов кластеризации позволяют строить изображения кластерных деревьев, которые, однако, обладают рядом недостатков.
При разработке процедуры кластеризации большого объема данных автор исходил из следующих требований к формату изображения кластерного дерева: 1 – базовым элементом рисунка, в котором изображается сегмент кластерного дерева, является круговой сектор; 2 – угловая мера сектора, выделяемого для изображения поддерева, пропорциональна числу узлов дерева в нем; 3 – радиус сектора, выделяемого для изображения поддерева, пропорционален количеству ярусов в данном поддереве.
На рис. 1 изображено кластерное дерево, построенное при помощи разработанной автором программы. Здесь 
– параметр высоты ребер кластерного дерева, T – узел кластерного дерева. Выделяемое пространство для изображения элементов кластерного дерева зависит от числа элементов его поддеревьев. Узел T кластерного дерева изображается кругом, радиус которого обратно пропорционален доле узлов поддерева, находящихся на данном ярусе, в общем числе узлов дерева. Высота ребер кластерного дерева прямо пропорциональна количеству узлов, расположенных на нижнем ярусе по отношению ко всем узлам кластерного дерева. На рис. 1 видно, что высота яруса 
меньше высоты нижнего яруса 
, а радиусы узлов 
,
,
также существенно различаются.
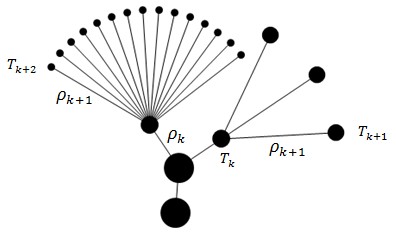
Рис. 1. Фрагмент кластерного дерева
Здесь – параметр высоты ребра, 
– обозначение узла кластерного дерева.
2. Описание разработанной программы: основные функции
Для реализации процедуры кластерного анализа в среде Mathematica 9.0 исследователем задается необходимый массив данных в виде матрицы, которую всюду в дальнейшем мы будем обозначать через m. Одним из важнейших параметров является уровень значимости p, который классифицирует расстояния между объектами массива данных. Исследуемые объекты считаются «близкими», если расстояние между ними не превышает уровня значимости p. Параметр p задается произвольно пользователем. При этом пользователь имеет возможность задавать собственную произвольную функцию расстояния, что не предусмотрено в пакетах прикладных программ специализированного назначения.
Перечислим основные функции, реализованные автором в пакете, предназначенном для выполнения кластерного анализа большого объема данных.
Функция dist является функцией расстояния, определяемой пользователем. Пользователь имеет возможность выбрать одну из перечисленных функций, либо задать собственную.
Переменная T представляет собой вложенный список, отражающий структуру кластерного дерева. Функция Draw Cluster Tree [T_, x_, y_, α_, β_,
_] – строит элементарный блок дерева, представляющий собой ветвь дерева, состоящую из узла и делящийся на несколько ветвей нижний ярус.
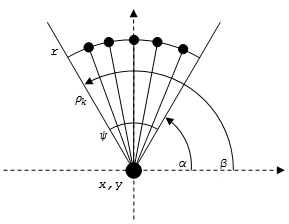
Рис. 2. Изображение элементарного блока кластерного дерева
Здесь x,y– координаты верхнего узла кластерного дерева; r – высота сторон сектора, выделяемого для изображения кластерного дерева; 
– параметр высоты ребер элементарного блока дерева; β, α – углы между осью абсцисс и сторонами сектора; 
– угол сектора, выделяемого для изображения кластерного дерева.
Высота ребра вычисляется по формуле:
,
здесь – параметр высоты ребра поддерева; vertices []– процедура подсчета узлов T на заданном ярусе k, vertices [
]– процедура подсчета всех узлов T кластерного дерева.
Функция Draw Cluster Tree имеет список вспомогательных внутренних переменных: {data, vertex Radius, ρ, φ, ψ, θ, z, w, s, t, T2, γ, δ}, основная функция которых основывается на рекурсивном построении всех элементов кластерного дерева.
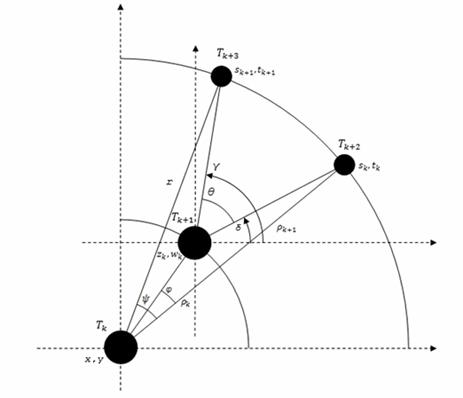
Рис. 3. Формирование фрагмента кластерного дерева
Здесь x,y - координаты верхнего узла кластерного дерева; 
- координаты узлов нижних ярусов поддерева; δ,γ – углы от оси абсцисс до ребер поддерева; 
– угол между ребрами поддерева; ψ - угол сектора, выделяемого для изображения кластерного дерева; φ – угол между ребрами кластерного дерева; - параметр высоты ребра поддерева; r - высота сторон сектора, выделяемого для изображения кластерного дерева.
Радиус узлов обратно пропорционален доле узлов поддерева, находящихся на данном ярусе, в общем числе узлов дерева и вычисляется по формуле:
,
здесь r - высота сторон сектора, выделяемого для изображения кластерного дерева; β, α – углы между осью абсцисс и сторонами сектора, vertices []– процедура подсчета узлов T на заданном ярусе k.
– угол между ребрами кластерного дерева, так же как и радиус узлов, имеет обратно пропорциональную зависимость и вычисляется по формуле:
,
здесь 
– угол между ребрами кластерного дерева; β, α – углы между осью абсцисс и сторонами сектора, vertices []– процедура подсчета узлов T на заданном ярусе k, vertices []– процедура подсчета всех узлов T кластерного дерева.
Координаты узлов и углов между ребрами поддерева имеют рекурсивный вызов и вычисляются по формулам:
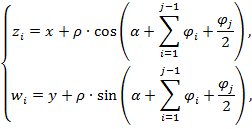
здесь
- координаты узлов поддеревьев; x,y - координаты верхнего узла дерева; – угол между ребрами кластерного дерева; - параметр высоты ребра поддерева;
Формулы для нахождения угла от оси абсцисс до ребер поддерева k+1.
,
,
,
здесь δ, γ – углы от оси абсцисс до ребер поддерева;
–угол между ребрами поддерева;;
- координаты узлов поддеревьев.
Описанные функции позволяют оптимально использовать отведенное для графика место, удовлетворяя требования, предъявленные к формату изображения кластерного дерева.
3. Примеры построения кластерных деревьев с помощью реализованной автором программы
На рис. 4 изображены кластерные деревья с различными исходными данными параметров m, p и dist.
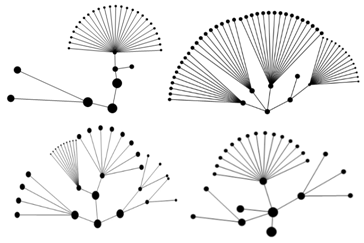
Рис. 4. Кластерные деревья с различными исходными данными параметров m, p и dist.
4. Анализ данных предприятия розничной торговли
Для тестирования программы была рассмотрена таблица параметров предприятия интернет – торговли, характеризующих продукцию по четырем параметрам: качество материалов, качество пошива, узнаваемость бренда и спрос. Каждый параметр оценивается специалистом по десятибалльной шкале.
Данные таблицы в матричной форме имеют вид:
m = {10,9,6,9},{10,9,4,8},{10,9,4,9},{8,8,6,7},{10,9,6,9} ,{10,9,6,8},{10,9,7,8},{10,9,5,8},{8,8,6,7},{8,8,5,7},{8,8,5,7},{10,9,6,8},{10,9,5,7},{10,9,4,7},{10,9,5,7},{6,7,9,9},{6,7,9,8},{6,7,9,9},{6,7,9,9},{6,7,4,9},{6,6,9,9},{6,6,9,9},{6,6,8,9},{6,6,3,7},{6,6,9,9},{6,6,5,8},{6,6,6,8},{6,6,5,7},{6,6,6,8},{6,6,5,8},{6,6,6,8},{6,6,4,8},{6,6,4,7},{6,6,5,7},{10,9,8,10},{9,9,7,8},{10,9,9,9},{8,9,7,8},{8,9,8,9},{7,6,3,3},{8,9,9,9},{10,9,8,9},{8,9,6,9},{9,9,8,9},{10,9,7,10},{10,9,8,9},{10,9,8,9},{10,8,9,9},{10,8,9,9}}.
Функция расстояния dist задана как сумма расстояний Евклида и расстояния городских кварталов (манхэттенского расстояния):dist[{{a_, b_, c_, d_}, {k_, j_, m_, n_}}] := Sqrt [(a - k)^2 + (b - j)^2 + c - m)^2 + (d - n)^2] + Abs[a - k] + Abs[b - j] + Abs[c - m] + Abs[d - n].
Исследуемые объекты считаются «близкими», если расстояние между ними не превышает уровня значимости p. Параметр p задается произвольно пользователем. В данном случае параметр определяется значением p = 0.5.
На рис.5. видно образование совокупностей, каждый из которых обладает общими свойствами. Также при дальнейшем исследовании полученных результатов можно выявить существенные факторы, влияющие на товарооборот предприятия интернет-торговли, и получить функциональное уравнение, описывающее эту зависимость.
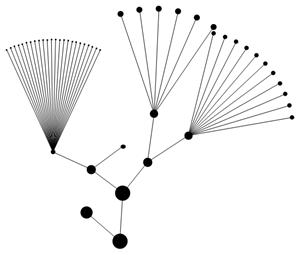
Рис. 5. Кластерное дерево таблицы оценки качества продукции
Выводы
Предложенный в работе алгоритм изображения кластерного дерева для большого объема данных и его программная реализация в системе компьютерной алгебры Mathematica 9.0 позволяют эффективно решать задачу разделения множества исследуемых объектов по их существенным признакам с применением определяемой пользователем метрики в пространстве их параметров.
Рецензенты:
Садыков Т.М., д.ф.-м.н., профессор кафедры Вычислительных систем и телекоммуникаций факультета математической экономики и информатики Российского экономического университета им. Г.В. Плеханова, г. Москва.
Родионов В.Н., д.ф.-м.н., профессор кафедры информатики Российского экономического университета им. Г.В. Плеханова, г.Москва.
Библиографическая ссылка
Нормов А.И. ИЗОБРАЖЕНИЕ КЛАСТЕРНОГО ДЕРЕВА ДЛЯ БОЛЬШОГО ОБЪЕМА ДАННЫХ В СРЕДЕ MATHEMATICA 9. 0 // Современные проблемы науки и образования. – 2014. – № 5. ;URL: https://science-education.ru/ru/article/view?id=14799 (дата обращения: 25.04.2024).