Рассматривается гибкая шарнирно опертая железобетонная колонна, нагруженная силой 
(рис. 1).
Для любого сечения железобетонного стержня можно записать следующие интегральные условия:
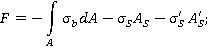(1)
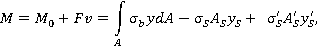(2)
где 
, если сила приложена с эксцентриситетом 
, или 
, если стержень имеет начальную погибь 
; 
— напряжения в бетоне; 
— напряжения в наименее сжатых арматурных стержнях площадью 
; 
— напряжения в наиболее сжатой арматуре площадью 
; 
и 
— координаты арматурных стержней (см. рис. 1).
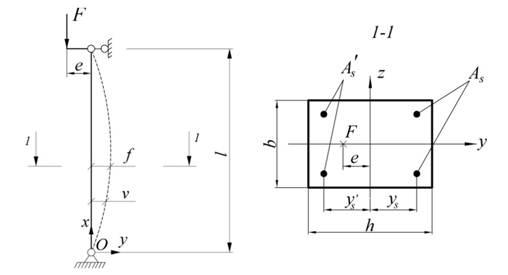
Рис. 1. Расчетная схема и поперечное сечение колонны
Полная деформация бетона представляет собой сумму осевой деформации 
и изгибной деформации, обусловленной изменением кривизны:
(3)
где 
— кривизна стержня.
Деформации бетона и арматуры должны быть равны между собой, откуда:
(4)
В модели упруго ползучего тела, полная деформация бетона представляется в виде суммы упругой деформации 
и деформации ползучести 
:
(5)
где 
— модуль упругости бетона, 
— напряжения в бетоне.
Из (5) напряжение в бетоне выражается:
(6)
А для напряжений в арматуре при условии 
:
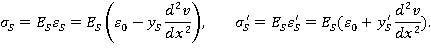(7)
После подстановки (6) и (7) в (2) для случая симметричного армирования (
и 
), основное разрешающее уравнение принимает вид:
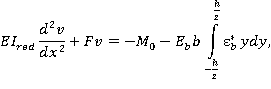(8)
где 
— приведенная жесткость поперечного сечения при изгибе; 
— момент инерции бетона; 
— момент инерции арматуры.
Величина определяется подстановкой (6) в (1):
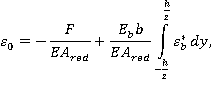(9)
где 
— приведенная жесткость поперечного сечения при растяжении–сжатии.
В качестве уравнения, связывающего деформации ползучести и напряжения, в данной статье будет рассмотрена упрощенная нелинейная теория ползучести нестареющего бетона Ю. А. Гурьевой [2, 3]. Согласно [2] деформация ползучести бетона представляется в виде суммы линейной и нелинейной составляющей:
где 
— линейная составляющая, определяемая так же, как и в теории Арутюняна–Маслова [1].
Выражение для скорости роста нелинейной составляющей ползучести 
имеет вид:
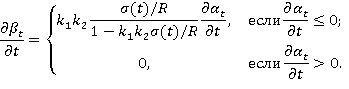(10)
Сжимающие напряжения в выражение (10) подставляются со знаком «+». Произведение коэффициентов 
и 
обычно полагается равным 1.
Если мера ползучести представляется в виде: 
, то для скорости роста линейной составляющей можно записать:
Методика решения задачи. Поперечное сечение разбивается по высоте на 
частей. На первом этапе решается упругая задача (
, 
). Решение уравнения (8) выполняется методом конечных разностей. Временной интервал, на котором рассматривается процесс ползучести, разбиваем на 
шагов 
. Определив прогиб в каждой точке, можно вычислить по формуле (6) напряжения, и далее определяются скорости роста составляющих деформации ползучести. Деформация ползучести в следующий момент времени находится при помощи линейной аппроксимации:
Решена задача для железобетонного стержня при следующих исходных данных: бетон класса B25, модуль упругости бетона 
, призменная прочность 
, предельная характеристика ползучести 
, 
, 
, сечение 
, арматура 4ø18 A400, модуль упругости арматуры 
, предел текучести арматуры 
, коэффициент армирования 
, 
, 
, 
, 
. Рассматривается интервал времени 
Сечение по высоте разбивается на 50 частей, временной интервал разбивается на 100 шагов.
На рис. 2 показан график изменения относительных напряжений 
в середине пролета. Сплошная линия — решение по нелинейной теории; штриховая — по линейной теории. Видно, что напряжения в арматуре существенно возрастают и по нелинейной теории при таких исходных данных могут достигать величины предела текучести.
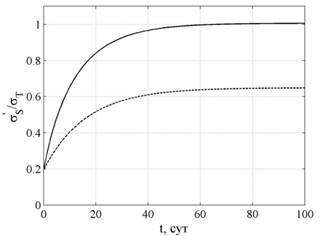
Рис. 2. Изменение относительных напряжений в арматуре
По действующим нормам [5] при эксцентриситете продольной силы 
и гибкости 
расчет по прочности внецентренно сжатых элементов прямоугольного сечения допускается производить из условия:
где 
— предельное значение продольной силы, которое может воспринять элемент, определяемое по формуле:
(11)
В рассматриваемом случае 
, 
, т.е. использовать формулы для центрального сжатия допускается. Гибкости 
соответствует значение коэффициента продольного изгиба 
. Для бетона В25 при коэффициенте 
, учитывающем длительное действие нагрузки, расчетное сопротивление 
. Арматуре А400 соответствует величина расчетного сопротивления при сжатии 
. Подставляя эти значения в формулу (11):
Полученное значение предельной нагрузки больше того, которое рассматривалось в задаче (980 кН) почти на 40%. Таким образом, одного коэффициента 
для учета длительного действия нагрузки недостаточно. Также величина 
оказалась не такой уж маленькой, чтобы ей пренебрегать.
На рис. 3 приводится график роста прогиба стержня. Скорость роста прогиба с течением времени затухает, т.е. потери устойчивости при ползучести в данном случае не происходит.
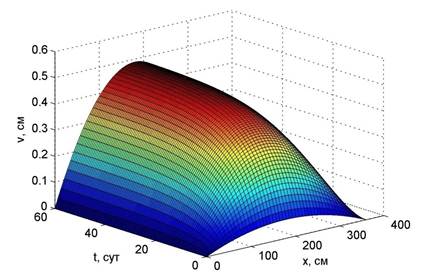
Рис. 3. График роста прогиба
Распределение напряжений по высоте сечения при 
приводится на рис. 4. Штриховой линией показано упругое решение, сплошной — результат по нелинейной теории при 
, штрихпунктирной — результат по линейной теории в тот же момент времени. Знаку «+» на рис. 4 соответствует сжатие. По нелинейной теории напряжения в бетоне в конце процесса ползучести оказываются меньше, чем по линейной.
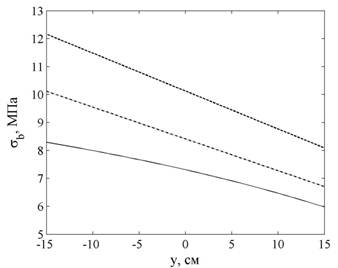
Рис. 4. Распределение напряжений по высоте сечения при x=l/2
На рис. 5 приводится изменение во времени линейной составляющей ползучести 
, нелинейной составляющей , полной деформации ползучести 
, упругой деформации и полной деформации 
при 
. Знаку «+» также соответствуют деформации сжатия.
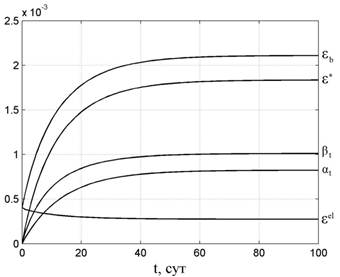
Рис. 5. Изменение деформаций во времени
Из рис. 5 видно, что нелинейная составляющая ползучести преобладает над линейной, кроме того, упругая деформация с течением времени уменьшается, и ее вклад в общую деформацию к концу процесса ползучести невелик. Нелинейная составляющая является полностью необратимой, и поэтому после снятия нагрузки в колонне возможно появление остаточных растягивающих напряжений. Такой эффект для центрально сжатых колонн был описан в работе [4].
Рецензенты:
Соболь Б.В., д.т.н., профессор, зав. кафедрой «Информационные технологии» Донского государственного технического университета», г. Ростов-на-Дону.
Панасюк Л.Н., д.т.н., профессор, зав. кафедрой «Техническая механика» ФГБОУ ВПО «Ростовский государственный строительный университет», г. Ростов-на-Дону.
Библиографическая ссылка
Юхнов И.В., Языев Б.М., Чепурненко А.С., Литвинов С.В. ПРОДОЛЬНЫЙ ИЗГИБ ГИБКОЙ ЖЕЛЕЗОБЕТОННОЙ СТОЙКИ ПРИ НЕЛИНЕЙНОЙ ПОЛЗУЧЕСТИ // Современные проблемы науки и образования. – 2014. – № 5. ;URL: https://science-education.ru/ru/article/view?id=14705 (дата обращения: 25.04.2024).