Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы

Романов В.П., Соколова Н.А.

Показано, что знанию человека, являющемуся продуктом сознания, свойственны неопределённость и случайность. В связи с этим для описания поведения учащегося в процессе обучения в высшем учебном заведении использован вероятностно-статистический метод, в соответствии с которым каждый учащийся идентифицируется функцией распределения, определяющей вероятность нахождения его в некоторой области информационного пространства. Получено аналитическое решение уравнения непрерывности для функции распределения индивидуума, движущейся в информационном пространстве с произвольной зависимостью средней скорости от координаты. Ключевые слова: учащийся, знание, случайность, информация, информационное пространство, плотность вероятности, функция распределения, вероятностно-статистическая модель.

Статья в формате PDF

173 KB

Введение

В настоящее время вопросы анализа состояния и прогнозирования развития системы образования в целом и учебно-воспитательного процесса (УВП) в любом учебном заведении приобретают чрезвычайно важное значение. Это обусловлено рядом причин, основная из которых та, что образование, являясь в известной степени консервативным, не удовлетворяет современным требованиям научно-технического прогресса. Часто говорят даже о кризисе образования в современном мире. При прогнозировании тенденций развития образования нередко ограничиваются лишь абстрактным теоретизированием и широкими обобщениями, далёкими от реальной действительности. В связи с этим мероприятия, проводимые по совершенствованию системы образования, в большинстве случаев оказываются малоэффективными.

Добиться положительного эффекта при проведении мероприятий, направленных на совершенствование системы образования, можно лишь в случае разработки концепции развития образования, основанной, прежде всего, на знании того, что такое «учащийся» в широком понимании этого термина и как он взаимодействует, например, с профессорско-преподаватель-ским коллективом высшего учебного заведения в процессе получения образования. Концепция должна также включать стратегию реформирования структуры системы образования, направленную на обеспечение оптимальных условий для реализации творческих возможностей каждым учащимся. Данная работа посвящена обоснованию и развитию вероятностно-статистической модели учащегося [1, 2], позволяющей проводить анализ и прогнозирование состояние УВП в высшем учебном заведении, на основании которых предлагать меры по совершенствованию структуры системы высшего образования.

Характер человеческого знания

Учение как вид деятельности, цель которого приобретение человеком знаний, умений и навыков, зависит от уровня развития сознания учащегося. Исследование явлений человеческого сознания представляет собой чрезвычайно трудную задачу. Это связано с принципиальной непосредственной ненаблюдаемостью его механизмов. Ученые, придерживающиеся материалистических взглядов, считают сознание свойством высокоорганизованной материи (мозга человека) давать идеальное отражение реального мира и его представление в виде обобщённых образов и понятий. В структуру сознания входят такие познавательные процессы, как ощущение, восприятие, память, мышление, воображение. Анализ этих процессов показывает, что им присущи элементы неопределенности и случайности, обусловленные принципиальной невоспроизводимостью в полном объёме психосоматического состояния индивидуума и параметров внешней среды от эксперимента к эксперименту, а также физиологическим, психологическим и информационным шумами при работе головного мозга. Последнее привело при описании процессов мышления к отказу от использования модели детерминистской динамической системы в пользу модели случайной динамической системы [3].

Из сказанного выше следует, что детерминизм сознания, проявляющийся в объективном отражении реальности в мозге человека, реализуется через случайность. Отсюда можно заключить, что знания человека, являющиеся фактически продуктом сознания, также имеют случайный характер. Это утверждение не противоречит жизненному опыту. Действительно, при первом знакомстве человека с тем или иным предметом (явлением) объём информации, усвоенный индивидуумом, может быть весьма скудным, причём он зависит от уровня развития сознания, физиологического и психического состояния человека, внешних условий и интервала времени ознакомления. При повторном изучении данного объекта к информации, систематизированной индивидуумом, добавляется новая информация, которая даже может привести к коренному изменению представлений об объекте исследований. В результате этого объём и глубина знаний увеличиваются. С течением времени, когда человек не работает с данным объектом, объём и глубина знаний о нём уменьшаются. Это связано с целым рядом причин, например, при переходе информации в долговременную память происходит её частичная потеря, индивидуум не в состоянии в нужный момент времени извлечь всю необходимую информацию из долговременной памяти, на микроуровне идёт процесс разрушения некоторых синаптических связей, ответственных за хранение информации об объекте и т. п. Процессы познания протекают строго индивидуально. Об этом свидетельствует тот факт, что объём и глубина знаний, усвоенных учащимися в одних и тех же внешних условиях, различны. Из вышесказанного можно заключить, что для описания процесса познания может быть использован вероятностно-статистический метод.

Модель поведения индивидуума в процессе обучения

Под термином «знание» будем понимать количество информации, усвоенной индивидуумом в процессе размышлений и рассуждений. В процессе обучения человек фактически движется в информационном пространстве. Однако указать точное положение учащегося в информационном пространстве невозможно, так как знание несёт в себе элемент случайности. Следовательно, можно говорить лишь о вероятности нахождения индивидуума в той или иной области информационного пространства. Учитывая вероятностный характер знания человека, в качестве объективной характеристики, определяющей поведение индивидуума в процессе обучения, может быть принята функция распределения (плотность вероятности), т. е. вероятность найти положение учащегося в единичной области информационного пространства. Каждый студент обладает индивидуальными свойствами, то есть допускается независимая локализация (пространственная и кинематическая) индивидуумов друг относительно друга в фазовом информационном пространстве. В этом случае функция распределения для коллектива индивидуумов может быть введена следующим образом [1, 4]:

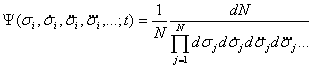,                                 (1)

где  - функция распределения индивидуумов в фазовом информационном пространстве;  - координаты индивидуумов в информационном пространстве;  - скорости учащихся; ,  и т. д. - ускорения первого, второго и т. д. порядков соответственно; N- общее число учащихся;dN- число индивидуумов в фазовом пространстве объёма ; t- время.

Функция распределения удовлетворяет условию нормировки, которое означает, что вероятность найти индивидуумы во всем фазовом информационном пространстве равна единице:

.

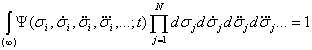Используя свойство аддитивности функции распределения по отношению к различным кинематическим свойствам индивидуумов, можно показать, что функции распределения меньшего числа измерений естественным образом связаны с функциями распределения бóльшего числа измерений:

,

,

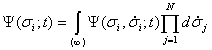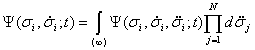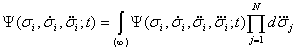,    (2)

Свойство аддитивности функций распределения позволяет также получить выражения, связывающие функцию распределения для каждого индивидуума с функцией распределения для всей системы:

,

,

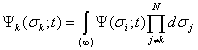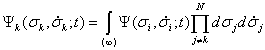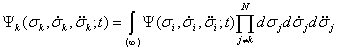,   (3)

где , ,... - функции распределения различного числа независимых переменных для k-го индивидуума.

Из (3) следует, что каждый индивидуум в информационном фазовом пространстве фактически представляется в виде некоторой функции распределения, содержащей информацию о разбросе координат и кинематических величин - скоростей и ускорений всех порядков.

Закон сохранения числа индивидуумов позволяет записать дифференциальные уравнения в виде уравнений непрерывности, описывающих эволюцию функций распределения:

,

, (4)

Система уравнений (4) ещё не представляет замкнутого аппарата для решения практических задач, так как помимо конкретизированных независимых переменных содержит и неконкретизированные величины, например,  для функции распределения ,  для функции распределения  и т. д. Применим к уравнениям (4) операции интегрирования типа

,         .

В результате после несложных преобразований, аналогичных [4], будем иметь

,

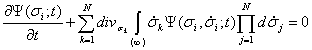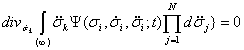,(5)

Система уравнений (5) представляет собой бесконечную цепочку зацепляющихся уравнений, каждое из которых связывает между собой две функции распределения меньшего и бóльшего количества переменных. Для обрыва этой цепочки уравнений воспользуемся дополнительной информацией, которую может дать опыт, а именно, информацией о средних значениях величин скорости  и ускорений первого , второго  и более высоких порядков:,

,

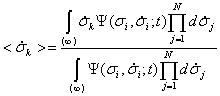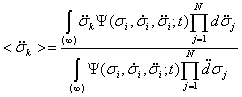(6)

Учитывая (2) и (6), преобразуем (5) к виду

,

,(7)

Система уравнений (7) в отличие от (5) не является системой зацепляющихся уравнений. Каждое из уравнений (7) может быть решено самостоятельно, если известны ,  и т. д. соответственно. Следует отметить, что обрыв цепочки зацепляющихся уравнений ведёт к потере информации о разбросе ускорений, начиная с некоторого порядка. Из всех уравнений системы (7) лишь первые два, по-видимому, допускают аналитические решения. Проведём подробный анализ первого уравнения из системы (7):

.                           (8)

Воспользуемся свойством аддитивности функции распределения для системы индивидуумов  по отношению к функциям распределения отдельных индивидуумов:

.                                       (9)

Подставляя (9) в (8), получим

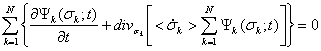.             (10)

Из (10) непосредственно следует, что уравнение непрерывности для функции распределения k-го индивидуума имеет вид

.                       (11)

С другой стороны уравнение непрерывности для функции распределения k-го индивидуума может быть записано в виде

,                          (12)

где

.

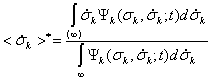Из сравнения (11) и (12) следует, что

.

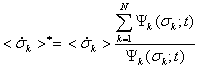Введём следующие переобозначения:

.

Тогда уравнение непрерывности (12) для функции распределения любого произвольно взятого индивидуума примет следующий вид:

.                                    (13)

Общее решение в координатном пространстве

Перепишем уравнение (13), раскрыв в нём слагаемое, относящееся к дивергенции плотности потока вероятности:

.                          (14)

Найдем общее решение уравнения (14) для произвольной зависимости средней скорости от координаты. Воспользуемся методом Фурье. С этой целью представим  в виде произведения двух функций, одна из которых  зависит только от координаты, а другая  - только от времени:

.                                                 (15)

Подставляя (15) в (14), после несложных преобразований будем иметь

.                    (16)

В левой части полученного уравнения стоит функция, зависящая только от t, а в правой части только от σ, и, следовательно, равенство возможно лишь в том случае, если левая и правая части равны одной и той же постоянной, обозначим которую буквой β. В этом случае уравнение (16) распадается на два уравнения:

          и          ,

общие интегралы которых имеют вид

       и          ,                 (17)

где A и B - постоянные интегрирования.

Подставляя (17) в (15), получим

,                              (18)

где  - новая постоянная интегрирования, соответствующая данному значению β.

Общее решение для индивидуальной функции распределения можно представить как суперпозицию решений (18):

,                        (19)

где  - постоянная интегрирования, зависящая от β, и нормированная на единичный интервал β.

Анализ решений (18) и (19) показывает, что выполнение условия нормировки

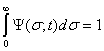
возможно только в том случае, когда  является чисто мнимой величиной. Обозначим , где ω - действительная величина,  - мнимая единица. Тогда решение (19) примет вид

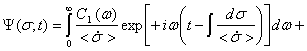
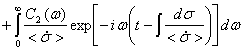,                                (20)

где  и  - постоянные интегрирования, зависящие от ω, и нормированные на единичный интервал ω.

Для получения решения (20) в явном виде необходимо знать зависимость  от . Рассмотрим интересный с теоретической и практической точек зрения случай, когда средняя скорость движения учащегося в информационном пространстве не зависит от координаты ( ).

В этом случае уравнение (14) принимает вид

,                                (21)

а общее решение (20) может быть легко преобразовано к виду

,

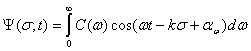где  - волновое число;  - постоянная интегрирования, зависящая от ω, и нормированная на единичный интервал частот;  - начальная фаза для частоты ω.

Из (21) непосредственно следует, что его решением должна быть функция аргумента , т.е. . В этом легко убедиться, подставив данную функцию в (21). Явный вид функции распределения  может быть найден из (21), если известно начальное распределение плотности вероятности .

Выводы

1. Знания человека, являющиеся продуктом его сознания, обладают свойствами неопределённости и случайности, следовательно, измерить точно объём и глубину знаний учащегося не представляется возможным. Для решения этой задачи предлагается использовать вероятностно-статистический метод.

2. В процессе обучения индивидуум движется в информационном пространстве, в котором он идентифицируется функцией распределения, определяющей вероятность нахождения его в той или иной области пространства.

3. На основе решения уравнения непрерывности найдено аналитическое выражение функции распределения учащегося, распространяющейся в информационном пространстве и во времени для случая произвольной зависимости средней скорости от координаты.

СПИСОК ЛИТЕРАТУРЫ

• 1. Романов В.П., Гордиевич Л.А., Золочевский Ю.Б. Альтернативная структура системы непрерывной подготовки высшими учебными заведениями специалистов высокой квалификации // Деп. в НИИВШ, 01.09.88, № 1389 - 88 деп.
• 2. Вернер В.Д., Гордиевич Л.А., Золочевский Ю.Б., Романов В.П. Вероятностно-статистический метод анализа и прогнозирования состояния учебно-воспитательного процесса на различных этапах системы непрерывного образования // Теоретико-методологи-ческие и прикладные проблемы развития единой системы непрерывного образования: Материалы конференции / Отв. ред. Б.С. Гершунский. - М., изд. АПН СССР, 1990. - Часть 2. - С. 56-60.
• 3. Хренников А.Ю. Моделирование процессов мышления в р-адических системах координат. - М.: ФИЗМАТЛИТ, 2004. - 296 с.
• 4. Власов А.А. Статистические функции распределения. - М.: НАУКА, 1966. - 356 с.

Библиографическая ссылка