В настоящее время, в связи с интенсивным развитием вычислительной техники, для моделирования различных физических процессов широко используются численные методы. Сегодня они активно вытесняют натурные эксперименты, в силу в силу их высокой стоимости и малой гибкости. Особенно это относится к тем научным направлениям, где эксперименты занимают длительное время (1000 и более часов) при сложных условиях нагружения, например, высокой температуре (300 и более С). Одним из таких научных направлений является исследование поведения оболочечных конструкций. В Камышинском технологическом институте разработан и успешно используется расчетный комплекс для решения такого класса задач [1, 3, 4].
Несмотря на широкие возможности этого расчетного комплекса, все расчеты до настоящего времени проводились только для конструкций с заранее определенными геометрическими параметрами, а вопросы их оптимизации с целью увеличения несущей способности конструкций не рассматривались. Вместе с тем, сегодня ко всем машиностроительным конструкциям в первую очередь предъявляются требования максимальной прочности и долговечности при минимальных затратах на их создание.
Целью работы является построение методики оптимизации геометрической формы оболочек вращения определенной конструкции и реализация этой методики в виде расчетного комплекса. Под оптимизацией понимается приведение геометрической формы оболочки к такому виду, чтобы значения механических напряжений в любой ее точке при заданном значении нагрузки не превышали заранее заданной допускаемой величины. В качестве математического аппарата будут использованы стандартные уравнения теории тонких осесимметричных оболочек вращения [2].
Поставленную задачу можно разделить на три подзадачи:
- - построение геометрической модели оболочечной конструкции;
- - построение физической модели оболочечной конструкции;
- - собственно оптимизация геометрических параметров.
Сформулируем основные ограничения, которые будет иметь разрабатываемая методика в рамках поставленной задачи:
- - форма оболочки аппроксимируется отдельными участками, состыкованными между собой и представляющими элементарные геометрические фигуры. Предусматривается 5 вариантов таких фигур: в форме пластины, конуса, сферы, тора, цилиндра. Для каждого из них задаются соответствующие геометрические характеристики;
- - минимальный радиус закругления не должен быть меньше двадцатикратной толщины оболочки (условие тонкой оболочки);
- - оптимизация проводится в пределах упругой работы материала, то есть деформация материала может быть только обратимой, а в качестве допускаемого напряжения следует задавать либо предел упругости, либо предел текучести;
- - оболочка состоит из одного слоя изотропного материала;
- - влияние температуры непосредственно в уравнениях не учитывается, если его все же необходимо учесть, то исходные данные задаются для конкретной температуры;
- - внешним механическим воздействием может быть либо внутреннее давление, либо усилие, вызывающее перемещение торца оболочки, либо оба этих воздействия одновременно;
- - нагружение оболочки предполагается статическим, то есть все факторы воздействия задаются один раз и не изменяются во времени;
- - механические свойства материала не зависят от времени;
- - оптимизация оболочки производится только за счет изменения радиуса кривизны отдельных участков, все остальные параметры, такие как исходные геометрические размеры, толщина, механические характеристики материала предполагаются неизменными.
В таком виде разрабатываемая методика потребует минимум исходных данных, и при этом будет отвечать всем заявленным требованиям. Кроме того, в дальнейшем будет возможна модернизация этой методики с целью использования ее для решения более сложных задач.
В качестве примера геометрической модели оболочки будем рассматривать сосуд давления, фрагмент осевого сечения которого представлено на рис. 1. Там же показаны геометрические параметры, задаваемые при вводе исходных данных.
Для построения модели используется 2-мерная Декартова система координат. Осевое сечение оболочки разбиваем на
5 элементарных участков (на рисунке они обозначены римскими цифрами).
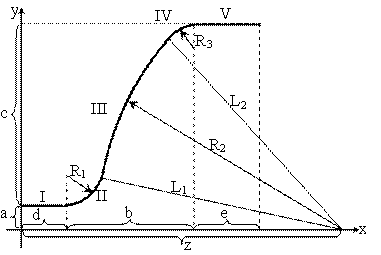
Рис. 1.
Исходными данными являются величины a, b, c, d, e, а величины R1, R2, R3 и z нужно определить.
Наиболее удобной формой представления физической модели или модели поведения осесимметричных оболочек является ее запись в виде системы уравнений для разрешающих функций [1-4]. Такая форма, во - первых, достаточно подробно изложена в справочной литературе, во - вторых, наиболее удобна для решения применительно к рассматриваемому классу задач. По результатам решения системы разрешающих уравнений вычисляются значения напряжений и деформаций в оболочке.
В конструкциях такого класса имеет место двух - или трехосное напряженное состояние, поэтому для его определения используют эквивалентное напряжение, вычисляемое по одной из теорий прочности, выбор которой зависит от свойств материала.
Таким образом, критерием оптимальности является условие, при котором эквивалентное напряжение σЭ в любой точке не превышает допускаемое σД:
σЭ ≤ σД.
Ограничения:
R1, R2, R3> 20 h; R1 + R3 < b,
где h - толщина оболочки.
Задача поиска оптимальных геометрических параметров конструкции сводится к поиску таких значений R1, R2 и R3, при которых действующие напряжения в конструкции не превышают допускаемое.
Блок-схема расчета оптимальных геометрических параметров конструкции приведена на рис. 2.
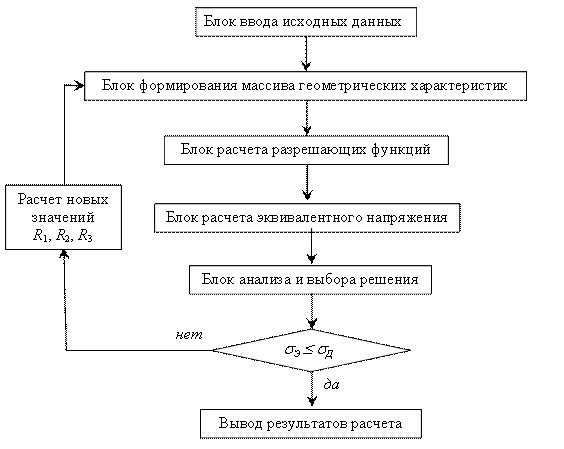
Рис. 2.
Процедура определения оптимальных геометрических параметров конструкции состоит в следующем.
1. Задаются исходные данные для расчета.
На начальном этапе величинам R1, R3 присваиваются начальные значения, равные двадцатикратному значению толщины оболочки.
2. Производится формирование массива необходимых геометрических характеристик для каждого из участков конструкции.
3. Вычисляется массив разрешающих функций оболочки.
4. Производится расчет меридиональных и окружных деформаций и напряжений. Затем определяется эквивалентное напряжение.
5. Производится анализ полученного поля напряжений. Если значение напряжений на каком - либо из участков превышает допускаемое, то производится пересчет формы данного участка, в частности, для сферического и тороидального участков необходимо увеличить радиус. Соответственно, на других участках, где напряжения ниже допускаемого, значение радиуса уменьшается. Выбор шага производится по адаптивному алгоритму, учитывающему, во сколько раз значение напряжения на текущем участке превосходят допускаемое. Это позволяет получить решение за наименьшее число шагов, кроме того, исключается возможность «блуждания» вокруг оптимального решения.
Затем процесс повторяется, начиная со второго шага.
Процесс поиска оптимальных значений радиусов прекращается как только на всех участках выполнится условие σЭ ≤ σД, если же данное условие не выполнятся на трех участках или не удается найти оптимальные радиусы, то поиск прекращается. В этом случае нужно либо увеличить толщину оболочки, либо задать другие механические свойства материалов.
Для реализации методики в виде расчетного комплекса был выбран математический пакет Mathcad 14.
На рис. 3. приведен результат расчета конструкции в Mathcad в виде изображения фрагмента осевого сечения, где пунктирной линией показано сечение исходной оболочки, а сплошной - оптимизированной.
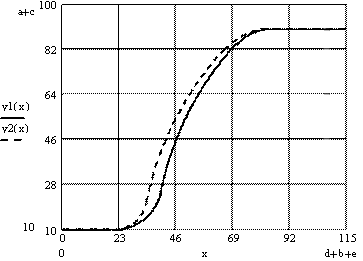
Рис. 3.
В результате была построена методика, позволяющая рассчитывать оптимальную геометрическую форму для нескольких классов оболочечных конструкций в пределах упругой работы материала. Принципы и подходы, реализованные в данной работе, могут быть использованы для разработки методики оптимального проектирования других типов конструкций, а также при более сложных характере внешнего воздействия и законе поведения материала.
СПИСОК ЛИТЕРАТУРЫ
- 1. Белов А.В. Осесимметричное упругопластическое напряженно-деформиро-ванное состояние оболочек вращения с учетом повреждаемости материала при ползучести: Автореферат дисс. канд. техн. наук. - Киев, 1989. - 18 с.
- 2. Методы расчета оболочек. Т.3. Теория упругопластических оболочек при неизотермических процессах нагружения / Ю.Н. Шевченко, И.В. Прохоренко. - Киев: Наук. думка, 1981. - 296 с.
- 3. Поливанов А.А. Осесимметричное упругопластическое деформирование многослойных оболочек вращения с учетом повреждаемости материала при ползучести: Автореферат дисс. канд. техн. наук. - Волгоград, 2004. - 19 с.
- 4. V. Bagmutov, A. Belov, A. Polivanov Damage Calculation Features of Multilayered Shells of Rotation at Thermo - Viscous - Elasto - Plastic Strain // MECHANIKA, 2004, No 3(47) - p. 19-23.
Библиографическая ссылка
Поливанов А.А. РАСЧЕТ ОПТИМАЛЬНЫХ ГЕОМЕТРИЧЕСКИХ ХАРАКТЕРИСТИК ОБОЛОЧЕЧНЫХ КОНСТРУКЦИЙ ПРИ СТАТИЧЕСКОМ НАГРУЖЕНИИ // Современные проблемы науки и образования. – 2009. – № 6-3. ;URL: https://science-education.ru/ru/article/view?id=1442 (дата обращения: 25.04.2024).



