Введение
Постоянное увеличение количества транспортных средств в условиях недостаточной пропускной способности дорог ведёт к затруднениям движения транспортных потоков. Интеллектуальные транспортные системы (ИТС) позволяют минимизировать образование заторовых ситуаций и увеличивать пропускную способность транспортной сети. Наработки в области ИТС примеряются для организации дорожного движения населённых пунктов и магистралей. Оптимизация управления дорожным движением достигается за счет взаимодействия управляющих, классифицирующих, прогнозирующих, экспертных, принимающих решения или поддерживающих эти процессы подсистем ИТС.
Несмотря на широкое распространение ИТС в настоящее время, адаптивное управление транспортными потоками используется ограниченно из-за сложности обработки в режиме реального времени возникающих на улично-дорожной сети ситуаций, влияющих на дорожное движение. В связи с этим стоит задача поиска методов обработки информации о нештатных ситуациях на улично-дорожной сети (УДС). Любые математические методы требуют в качестве входных данных конкретные величины. Таким образом, необходимо создание математической модели нештатных ситуаций, их классификация и выявление характеристик.
Моделирование УДС и нештатных ситуаций
Модель улично-дорожной сети в ИТС опишем ориентированным графом G в пространстве ![]() , представляющим собой совокупность непустого множества
, представляющим собой совокупность непустого множества ![]() вершин (узлов) графа, множества
вершин (узлов) графа, множества ![]() непрерывных самонепересекающихся кривых, называемых дугами графа, инциденторов
непрерывных самонепересекающихся кривых, называемых дугами графа, инциденторов ![]() и
и ![]() , сопоставляющих каждой дуге
, сопоставляющих каждой дуге ![]() начальную вершину
начальную вершину ![]() и конечную вершину
и конечную вершину ![]() , удовлетворяющих следующим условиям:
, удовлетворяющих следующим условиям:
- каждая незамкнутая кривая в
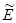 содержит ровно две точки множества
содержит ровно две точки множества 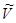 , которые являются ее граничными точками;
, которые являются ее граничными точками; - кривые в
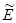 не имеют общих точек, за исключением точек из множества
не имеют общих точек, за исключением точек из множества 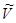 ;
; 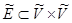 [1].
[1].
В модели, рассматриваемой в работе, используется специальный граф, вершины которого на перекрестке соответствуют стоп-линиям на подходах к перекресткам, на пешеходном переходе и железнодорожном переезде являются границами участка, на перегоне соответствуют границам участка и точкам возможного разветвления потоков, а дуги – всевозможным проездам транспорта по следующему за текущим участку УДС (рис. 1).
Такой подход к описанию позволяет адекватно отобразить различные типы конфигураций улично-дорожной сети, все особенности системы организации движения, учесть ограничения, связанные с запретами маневров отдельных транспортных средств, наличием одностороннего движения и т.п.
Триада объектов <участок>, <узел>, <дуга> является базисом концептуальной модели ИТС, все остальные объекты будут так или иначе привязаны к этому базису.
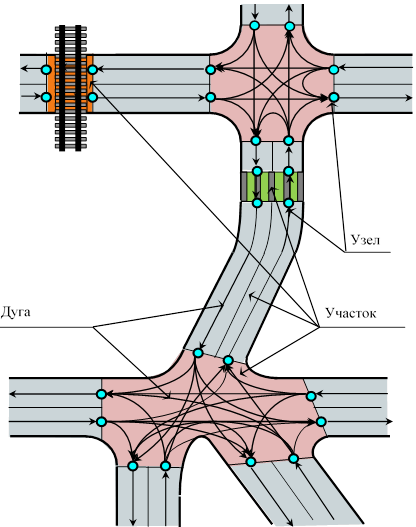
Рисунок 1. Графовая модель улично-дорожной сети
<Участок> – полигональный участок УДС, представленный набором координатных пар, описываемый единым набором физических параметров.
<Узел> – место разделения потоков транспортных средств. Узел является вершиной ориентированного графа, канализирующего транспортные потоки, всегда лежит на стыке двух участков и показывает возможность движения с одного участка на другой в направлении, определяемом соответствующей дугой. Двум соседним участкам поставлено в соответствие два узла.
<Дуга> – это элемент ориентированного графа, задающий направление движения ТП на участке и содержащий соответствующие характеристики (длина дуги, интенсивность движения в данном направлении, плотность потока и т.п.). Двум узлам поставлена в соответствие одна дуга, определяющая направление движения ТС, либо две дуги, определяющие место разворота (смены направления движения). По одному участку может проходить несколько дуг (потоков), но дуга может находиться только внутри единственного участка.
Разметкой дуг графа G назовем функцию ![]() . Такой граф является помеченным, а его элементы – пометками [2]. Пометка, являющаяся числом, является весом
. Такой граф является помеченным, а его элементы – пометками [2]. Пометка, являющаяся числом, является весом ![]() дуги
дуги ![]() , а граф G – нагруженным. Весом дуги графа улично-дорожной сети может быть число полос в каждом направлении, вид покрытия, интенсивность потока, тип регулирования и др. В зависимости от решаемой задачи вес дуги выбирается из заданного набора параметров объектов или вычисляется по формуле. В качестве пометки дуги графа УДС может выступать интеллектуальная функция, позволяющая принять решение в распределении транспортных потоков по сети. При решении задач классификации в качестве пометок дуги графа УДС могут выступать «качественные» (несравнимые) характеристики дуги: тип дуги «перекресток» не совпадает с типом дуги «пешеходный переход».
, а граф G – нагруженным. Весом дуги графа улично-дорожной сети может быть число полос в каждом направлении, вид покрытия, интенсивность потока, тип регулирования и др. В зависимости от решаемой задачи вес дуги выбирается из заданного набора параметров объектов или вычисляется по формуле. В качестве пометки дуги графа УДС может выступать интеллектуальная функция, позволяющая принять решение в распределении транспортных потоков по сети. При решении задач классификации в качестве пометок дуги графа УДС могут выступать «качественные» (несравнимые) характеристики дуги: тип дуги «перекресток» не совпадает с типом дуги «пешеходный переход».
Стохастическим графом УДС ![]() назовем нагруженный граф, на каждой дуге
назовем нагруженный граф, на каждой дуге ![]() которого находится пометка
которого находится пометка ![]() , определяющая вероятность
, определяющая вероятность ![]() возникновения события
возникновения события ![]() на дуге
на дуге ![]() .
.
Примером веса ![]() для задачи адаптивного управления транспортными потоками в условиях присутствия нештатных ситуаций на улично-дорожной сети может служить вероятность события, состоящего в том, что транспортное средство из узла
для задачи адаптивного управления транспортными потоками в условиях присутствия нештатных ситуаций на улично-дорожной сети может служить вероятность события, состоящего в том, что транспортное средство из узла ![]() , являющегося началом дуги УДС
, являющегося началом дуги УДС ![]() , поедет по этой дуге
, поедет по этой дуге![]() [3].
[3].
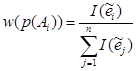 , где
, где ![]() – количество входящих в узел
– количество входящих в узел ![]() дуг;
дуг; ![]() – входящие в узел
– входящие в узел ![]() дуги. В случае отсутствия разделения транспортных потоков в узле
дуги. В случае отсутствия разделения транспортных потоков в узле ![]()
![]() .
.
Множество нештатных (критических) ситуаций на улично-дорожной сети ![]() – совокупность таких ситуаций, которые способны оказывать влияние на транспортные потоки и возникновение которых носит случайный характер. Нештатные ситуации характеризуются тем, что они не учитываются при разработке постоянной схемы организации дорожного движения [4]. Примерами нештатных ситуаций могут служить дорожно-транспортные происшествия (ДТП), посторонние предметы на проезжей части, дефекты дорожного покрытия, туман, строительные или ремонтные работы с перекрытием проезжей части и т.п. Модель нештатной ситуации представляется основными её характеристиками (рис. 2)
– совокупность таких ситуаций, которые способны оказывать влияние на транспортные потоки и возникновение которых носит случайный характер. Нештатные ситуации характеризуются тем, что они не учитываются при разработке постоянной схемы организации дорожного движения [4]. Примерами нештатных ситуаций могут служить дорожно-транспортные происшествия (ДТП), посторонние предметы на проезжей части, дефекты дорожного покрытия, туман, строительные или ремонтные работы с перекрытием проезжей части и т.п. Модель нештатной ситуации представляется основными её характеристиками (рис. 2)
Характеристики нештатных ситуаций
Вид нештатной ситуации ![]() . Множество K представляет собой набор всех возможных видов нештатных ситуаций. Примерами входящих в него элементов являются <ДТП>, <туман>, <упавшее дерево>, <ремонтные работы>, <открытый канализационный люк> и пр.
. Множество K представляет собой набор всех возможных видов нештатных ситуаций. Примерами входящих в него элементов являются <ДТП>, <туман>, <упавшее дерево>, <ремонтные работы>, <открытый канализационный люк> и пр.
Зона непосредственного воздействия нештатной ситуации ![]() ,
, ![]() – совокупность дуг графа УДС G и количество полос движения
– совокупность дуг графа УДС G и количество полос движения ![]() на них, затронутых нештатной ситуацией, а также коэффициент непосредственного воздействия на затронутые дуги
на них, затронутых нештатной ситуацией, а также коэффициент непосредственного воздействия на затронутые дуги ![]() .
. 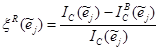 , где
, где![]() – номинальная пропускная способность дуги,
– номинальная пропускная способность дуги, ![]() – пропускная способность дуги в условиях нештатной ситуации на ней. Зона непосредственного воздействия определяет дислокацию нештатной ситуации на графе улично-дорожной сети.
– пропускная способность дуги в условиях нештатной ситуации на ней. Зона непосредственного воздействия определяет дислокацию нештатной ситуации на графе улично-дорожной сети.
. 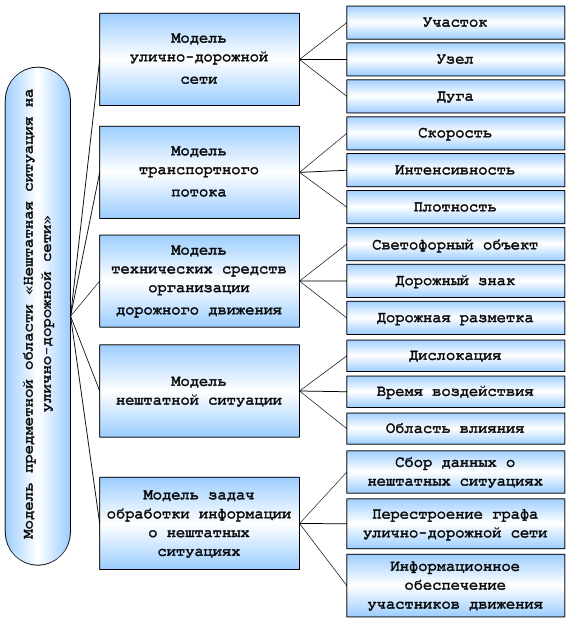
Рисунок 2. Декомпозиция предметной области «Нештатная ситуация на улично-дорожной сети»
Нештатная ситуация – событие динамическое, привязанное ко времени. Поэтому целесообразно введение таких параметров, как время возникновения критической ситуации ![]() и время устранения критической ситуации
и время устранения критической ситуации ![]() .
.
Математическое ожидание периода существования критической ситуации ![]() . Этот параметр важен во время существования нештатной ситуации, пока время
. Этот параметр важен во время существования нештатной ситуации, пока время ![]() неизвестно.
неизвестно.
Область влияния нештатной ситуации – подграф улично-дорожной сети ![]() , непустое множество вершин
, непустое множество вершин ![]() и дуг
и дуг ![]() , на которые оказывает влияние нештатная ситуация. Данный параметр зависит от характеристик нештатной ситуации, структуры графа УДС и весовых характеристик его дуг
, на которые оказывает влияние нештатная ситуация. Данный параметр зависит от характеристик нештатной ситуации, структуры графа УДС и весовых характеристик его дуг ![]() .
.
Классификация нештатных ситуаций
Методы обработки информации о нештатных ситуациях зависят от типа нештатной ситуации. На рисунке 3 приведена классификация нештатных ситуаций.
По пространственному расположению выделим точечные, линейные и площадные нештатные ситуации.
Точечная нештатная ситуация ![]() . Нештатную ситуацию назовем точечной, если её геометрические размеры пренебрежительно малы. Будем считать нештатную ситуацию точечной, если радиус окружности
. Нештатную ситуацию назовем точечной, если её геометрические размеры пренебрежительно малы. Будем считать нештатную ситуацию точечной, если радиус окружности ![]() , затронутый нештатной ситуацией участок проезжей части, не превышает 30 м. Точечная нештатная ситуация характеризуется географическими координатами (
, затронутый нештатной ситуацией участок проезжей части, не превышает 30 м. Точечная нештатная ситуация характеризуется географическими координатами (![]() ,
,![]() ).
).
Линейная нештатная ситуация ![]() отличается от точечной значительной протяжённостью. Назовем нештатную ситуацию линейной, если она непосредственно воздействует на один или несколько смежных участков УДС, при этом отсутствуют точки разделения и слияния транспортных потоков на этих участках. Линейная нештатная ситуация характеризуется географическими координатами граничных точек (
отличается от точечной значительной протяжённостью. Назовем нештатную ситуацию линейной, если она непосредственно воздействует на один или несколько смежных участков УДС, при этом отсутствуют точки разделения и слияния транспортных потоков на этих участках. Линейная нештатная ситуация характеризуется географическими координатами граничных точек (![]() ,
,![]() ),
),
(![]() ,
,![]() ).
).
Площадная нештатная ситуация ![]() оказывает воздействие на k смежных или несмежных участков УДС вне зависимости от наличия точек разветвления и слияния транспортных потоков. Для указания дислокации площадной нештатной ситуации не требуются географические координаты, достаточно указания зоны непосредственного воздействия с целью привязки к графу УДС.
оказывает воздействие на k смежных или несмежных участков УДС вне зависимости от наличия точек разветвления и слияния транспортных потоков. Для указания дислокации площадной нештатной ситуации не требуются географические координаты, достаточно указания зоны непосредственного воздействия с целью привязки к графу УДС.
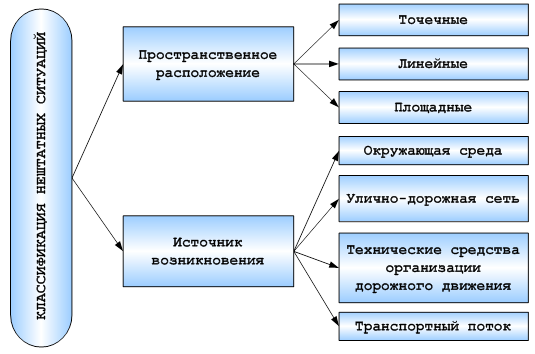
Рисунок 3. Классификация нештатных ситуаций
По источнику возникновения нештатные ситуации разделим на 4 класса:
- Нештатные ситуации, вызванные окружающей средой. К таким ситуациям отнесём туман, гололёд и т.п.
- Нештатные ситуации, вызванные изменениями улично-дорожной сети: разрушения дорожного покрытия, посторонние объекты на проезжей части (упавшее на проезжую часть дерево), ремонтные и строительные работы, затрагивающие проезжую часть.
- Нештатные ситуации, вызванные техническими средствами организации дорожного движения (ТСОДД). Примерами таких нештатных ситуаций служат неработающий светофор, нечитаемый дорожный знак и пр.
- Нештатные ситуации, вызванные транспортным потоком, – дорожно-транспортные происшествия.
Заключение
Таким образом, произведен обзор предметной области «Нештатная ситуация на улично-дорожной сети». Выявлены основные характеристики нештатных ситуаций, произведена их классификация. Полученная модель нештатной ситуации необходима для применения методов перестроения графа улично-дорожной [5] сети с целью поиска управляющих воздействия на транспортные потоки в режиме реального времени.
Рецензенты:
Титов Б.А., д.т.н., профессор, заведующий кафедрой организации и управления перевозками на транспорте, ФГБОУ ВПО «Самарский государственный аэрокосмический университет имени академика С.П. Королева (национальный исследовательский университет)», г. Самара.
Хайтбаев В.А., д.э.н., профессор кафедры организации и управления перевозками на транспорте, ФГБОУ ВПО «Самарский государственный аэрокосмический университет имени академика С.П. Королева (национальный исследовательский университет)», г. Самара.
Библиографическая ссылка
Осьмушин А.А., Богданова И.Г., Сидоров А.В. МОДЕЛИРОВАНИЕ НЕШТАТНЫХ СИТУАЦИЙ НА УЛИЧНО-ДОРОЖНОЙ СЕТИ // Современные проблемы науки и образования. – 2013. – № 6. ;URL: https://science-education.ru/ru/article/view?id=11766 (дата обращения: 26.04.2024).



