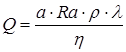Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Пестова О.В. 1 Пестов Д.А. 1 Шишеня А.В. 1

---

1 Южный федеральный университет

В работе построена и численно реализована математическая модель процесса массопереноса эманации радона в рыхлых отложениях и в приземном слое атмосферы с учетом диффузии и конвекции. Из физических соображений обоснованы начальные и граничные условия, приведен вывод условий на границе раздела двух сред. Построенная дискретная модель, основывающаяся на сетке с переменными шагами по пространству и по времени, сводится к системе с трехдиагональной матрицей, которая при условии выполнения требований к этому методу об устойчивости и сходимости решается методом прогонки. Построенная математическая модель позволяет в рамках решения одной задачи исследовать пространственно-временные распределения радона в земле и в атмосфере. В работе приведены результаты исследования пространственно-временных распределений радона с учетом различных физических условий.

Статья в формате PDF

728 KB

внутренние граничные условия

радон

моделирование

1. Куповых Г.В., Морозов В.Н., Шварц Я.М. Теория электродного эффекта в атмосфере : монография. – Таганрог : Изд-во ТРТУ, 1998. – 123 с.

2. Морозов В.Н. Математическое моделирование атмосферно-электрических процессов с учетом влияния аэрозольных частиц и радиоактивных веществ : монография / РГГМУ. – СПб., 2011. - 253 с.

3. Новиков Г.Ф. Радиометрическая разведка. - Л. : Недра, 1989. - 407 с.

4. Новикова О.В., Редин А.А., Болдырев А.С., Болдырева К.А., Пестов Д.А. Электродинамическая модель приземного слоя атмосферы с учетом массопереноса радона в грунте и над поверхностью земли // Научная мысль Кавказа. - 2012. - № 4. - С. 98-102.

5. Паровик Р.И., Ильин И.А., Фирстов П.П. Математическая диффузионная модель массопереноса радона (222Rn) в грунте и его эксхаляции в приземный слой атмосферы // Вестник Краунс. Сер.: Науки о земле. - 2006. - № 1. – Вып. № 7. – С. 110 – 114.

6. Радиоэкология : учебник для вузов / М.Г. Давыдов [и др.]. – Ростов н/Д : Феникс, 2013. – 635 с. : ил. – (Высшее образование).

7. Самарский А.А., Гулин А.В. Численные методы математической физики. - 2-е изд. - М. : Научный мир, 2003. - 316 с.

8. Boldyreff A., Kupovykh G., Redin A. Modeling of ionization–recombination processes in the atmospheric surface layer // Journal of Electrostatics. Elsevier. – 2013. – V. 71, Is. 3, June. – P. 305–311.

Введение

Наиболее значимый путь попадания радона (Rn-222) в атмосферу связан с его выделением непосредственно из грунтов, где он распространен крайне неравномерно. Это связано как с тем, что радон накапливается в тектонических неоднородностях, куда он поступает по системам микротрещин из горных пород, так и с их способностью аккумулировать радон и коэффициентом эманирования. Общепринято считать, что в динамике подпочвенного радона находит отражение изменение напряженно-деформированного состояния геосреды на последней стадии подготовки очага землетрясения [5]. Одновременно эксхаляция радона в приземный слой атмосферы приводит к его ионизации, которая изменяет проводимость приземного слоя и влияет на его электрические характеристики [8].

Построением математической конвективно-диффузионной модели массопереноса радона в грунте и его эксхаляций в приземный слой атмосферы занимались Паровник Р.И., Ильин И.А., Фирстов П.П. [5]. Задача решалась аналитически без учета конвективной составляющей, а коэффициент турбулентной диффузии в атмосфере считался постоянным. Исследования влияния радона на ионизацию атмосферы были проведены Куповых Г.В., Морозовым В.Н., Шварцем Я.М. [1; 2].

Постановка задачи. В данной работе построена конвективно-диффузионная модель массопереноса радона в рыхлых отложениях и его стока в приземный слой атмосферы. Система дифференциальных уравнений в частных производных, описывающих процессы массопереноса радона, имеют вид [3; 4]:

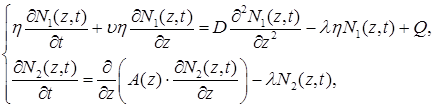(1)

Основные параметры системы (1) приведены в таблице 1 [5; 6]. Первое уравнение системы (1) описывает установившийся диффузионно-конвективный процесс массопереноса радона в грунте, а второе уравнение системы (1) диффузионный массоперенос радона в атмосфере.

Таблица 1 – Параметры системы

Дополним систему (1) следующими начальными и граничными условиями.

1. Равенство потоков и соотношение для концентраций радона на границе сред

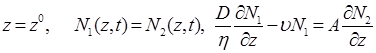. (2)

Здесь z0 – граница раздела «земля – атмосфера», z – вертикальная координата.

2. Постоянная концентрация радона при достижении равновесия с продуктами распада на определенной глубине рыхлых отложений

. (3)

Здесь ось z направлена вертикально, ноль находится на границе «земля – атмосфера».

3. Концентрация радона в начальный момент времени максимальна

. (4)

Условия на границе. Условие (2) было получено следующим образом. Поделим первое уравнение системы (1) на η. H = z0 – уровень почвы. Для корректной постановки задачи на границе раздела двух сред земли и воздуха поставим задачу в общей области «земля – атмосфера». В таком виде на границе двух сред (поверхности земли) появляется существенное внутреннее граничное условие (2). Для его постановки проинтегрируем первое уравнение системы (1) от –∞ до z0:

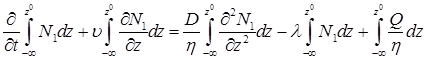. (5)

Значение направленного внутрь грунта потока массы радона через границу, за счет которого изменяется масса радона в грунте, примет вид:.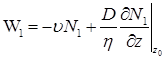

Проинтегрируем второе уравнение (для воздуха) системы (1) от z0 до +∞. Аналогичным образом запишем поток через границу в воздухе: .

В результате граничные условия имеют следующий вид:

при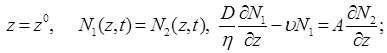

при (6)

при

Построение дискретной модели. Пусть коэффициент турбулентной диффузии зависит от высоты и имеет вид: . Введем функцию концентрации:

,

где θ – гладкая срезающая функция, такая что:

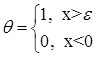, при .

Концентрацию радона в почве и в воздухе зададим в виде:

.

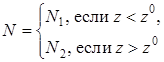Перепишем уравнения (1) в виде:

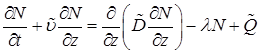. (7)

Здесь введены следующие обозначения:

концентрация радона:

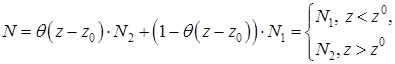, (7.1)

скорость конвективного переноса:

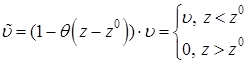, (7.2)

коэффициент диффузии:

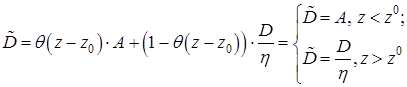, (7.3)

функция интенсивности ионообразования:

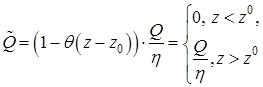. (7.4)

Граничные условия будут иметь вид:

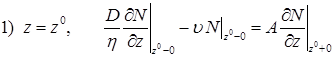
; (8)

;

3) .

Сетка. Для построения разностной схемы введем сетку в области изменения независимых переменных. Введем равномерную сетку по переменной z с шагом hz, которую обозначим:

,

где l – длина области, N – количество отрезков разбиения.

Также введем равномерную сетку по переменной t с шагом ht, которую обозначим:

.

Дискретная модель. Для решения дифференциального уравнения (7) используется интегро-интерполяционный метод, т.к. он сохраняет консервативность модели, а значит и непрерывность потока. Проинтегрируем уравнение (7), разбив его на два. Вначале возьмем интеграл от первого уравнения системы (1) по двум областям от до и от до .

Рассмотрим первый интеграл:

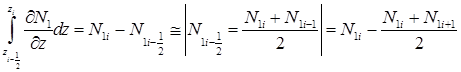. (9)

Аппроксимируем 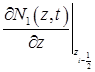центральной разностью:

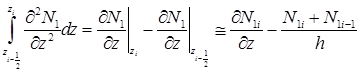. (10)

Рассмотрим второй интеграл:

.

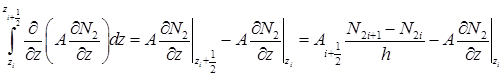Тогда для уравнения (7) получим следующую аппроксимацию уравнения на равномерной сетке по пространственной и временной координатам:

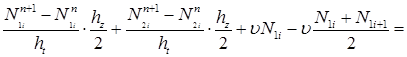(11)

.

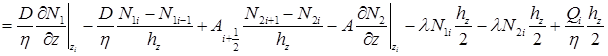Применяя условия (8), приходим к следующему уравнению:

.

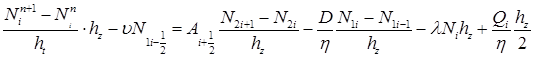Вычислив потоки на границе, для соответствующих уравнений, и используя известное соотношение (2) на границе «земля – атмосфера», получим уравнение для точек на границе. Как результат, новые условия на границе «земля – атмосфера» имеют следующую аппроксимацию на границе:

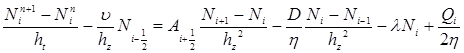, (12)

.

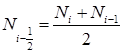Аппроксимация в остальных точках сетки. Запишем разностные схемы для аппроксимации уравнений (1) в точках сетки, кроме границы раздела «земля – атмосфера». Рассмотрим уравнение (7), которое в грунте примет следующий вид. Запишем разностную схему для этого уравнения:

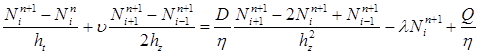(13),

В свою очередь разностная схема для уравнения в воздухе (7) будет иметь вид:

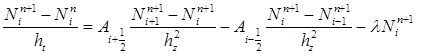(14)

Численный расчет был проведен при помощи метода прогонки [7]. Модель проверена на устойчивость при помощи метода максимума, получены следующие ограничения:

- на шаг по времени,

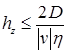- на шаг по пространству.

Из данных условий также следует еще одно возможное ограничение на шаг по времени: .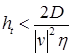

Моделирование и обсуждение. На основании уравнений (1) при условии выполнения (2)-(4) и с учетом параметров, приведенных в таблице 1, исследовалось распределение радона в грунте и в атмосфере. Исследования проводились при тестовых значениях в пределах глубин от 10 м до высот порядка 10 м при различных коэффициентах диффузии. Моделирование проводились при скорости конвективного переноса v = 0,1м/с. На рисунке 1 приведены графики распределения относительной концентрации радона в почве и в приземном слое атмосферы по тестовым данным.

Анализируя полученные результаты, получаем, что при увеличении коэффициента диффузии в почве концентрация радона уменьшается. Так, при изменении коэффициента диффузии от 10–2 см2/с до 15·10–3 см2/с на высоте 1 м концентрация радона уменьшится на 30%. Данные результаты хорошо согласуются с результатами, полученными в работе [5].

Характерный масштаб распределения радона составляет порядка 2 м. При
D = 10-2 см2/с в случае, если концентрация радона составляет порядка 100 кБк/м3 на глубине 10 м, то на уровне земли наблюдается выход радона концентрацией, равной 292 Бк/м3. При значениях концентрации радона менее 300 Бк/м3 на глубине 10 м выход радона на поверхность практически не наблюдается.

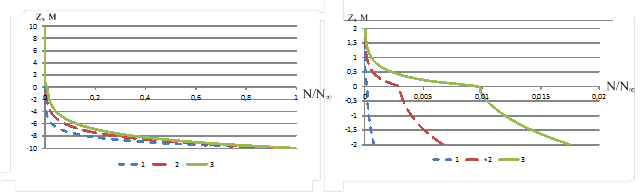
Рисунок 1. Зависимость относительной концентрации радона N/N∞ от высоты при различных значениях коэффициента диффузии в почве D: кривая 1 – 5·10-3 см2/с; кривая 2 – 10-2см2/с; кривая 3 – 15·10-3 см2/с.

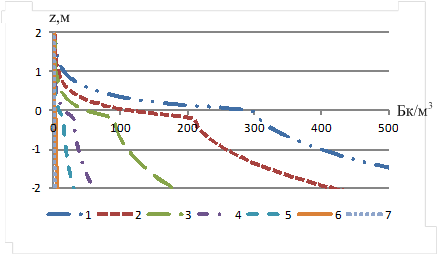
Рисунок 2. Профили концентрации радона в зависимости от максимальной концентрации радона на глубине 10 м: 1 – 100 кБк/м3; 2 – 70 кБк/м3; 3 – 30 кБк/м3; 4 – 10 кБк/м3; 5 – 5 кБк/м3; 6 – 1 кБк/м3; 7 – 300 Бк/м3.

Таким образом, в результате работы построена математическая модель массопереноса радона с обоснованием условия на границе раздела двух сред, построена численная схема решения и получены результаты, позволяющие исследовать пространственно-временные распределения радона в различных физических условиях.

Исследование выполнено при поддержке Министерства образования и науки Российской Федерации, контракт 14.132.21.1380 от 01.10.2012.

Рецензенты:

Жорник А.И., д.ф.-м.н., профессор, кафедра теоретической, общей физики и технологии Таганрогского государственного педагогического института им. А.П. Чехова, г. Таганрог.

Илюхин А.А., д.ф.-м.н., профессор, профессор кафедры математического анализа Таганрогского государственного педагогического института им. А.П. Чехова, г. Таганрог.

Библиографическая ссылка