Введение
В настоящее время биология и медицина стремительно отходят от вербального описания и основываются на математических моделях и информационных технологиях Успешное решение биомедицинских задач невозможно без создания соответствующих информационных систем. Одним из наиболее сложных и трудоемких процессов проектирования информационной системы является выявление закономерностей из имеющихся массивов данных. Он не всегда заканчивается успешно, поскольку базы данных содержат разнотипную, противоречивую и неполную информацию. Большинство существующих в настоящее время информационных технологий ориентированы на решение конкретных практических задач и являются узконаправленными, сложными, дорогостоящими, что делает их непригодными для массового применения в медицинских учреждениях. В связи с этим авторами разработана система, которая позволяет выявить закономерности временного изменения показателей биосистемы и включает такие важные сервисы, как восстановление пропусков в данных, выявление наличия сезонных ритмов, выделение трендов во временных рядах, определение сезонной декомпозиции.
Целью исследования является выявление закономерности временного изменения показателей биосистемы на основе статистического анализа.
Структура информационной медицинской системы
Для осуществления поставленной цели в информационной медицинской системе разработаны сервисы с применением распараллеленных вычислений. Среди них:
1. Сервис восстановления пропусков в исходных данных
Пусть значения показателей известны в моменты времени tj, j=1,…,n. Построим на временном интервале [t1, tn] функцию Sу(t), интерполирующую y=f(t) так, что на каждом произвольном отрезке [tj, tj+1], лежащем внутри интервала [t1, tn], функция Sу(t) являлась полиномом, а в узлах имела непрерывные производные.
В качестве Sу(t) выбран сплайн третьей степени, который в узлах tj имеет непрерывные 1-ю, и 2-ю производные, и на каждом из отрезков [tj, tj+1] принимает вид:
![]() ,
,
где yj – значение показателей в момент tj
bj, cj, dj – коэффициенты, подлежащие определению.
Требования непрерывности функции Sу(t), ее 1-й и 2-й производных, дает 3(n–2) условий для определения коэффициентов. Условия интерполирования в точке tn, приводят к соотношениям для вычисления коэффициентов![]() на разных интервалах аппроксимации:
на разных интервалах аппроксимации:
![]() ,
,
где ![]()
![]() , j =1 ,…, n – 1
, j =1 ,…, n – 1
![]() , j = 2 ,…, n–1
, j = 2 ,…, n–1
где ![]() ;
;
![]() .
.
Из краевых условий запишем уравнения следующего вида:
![]() ;
; ![]() ,
,
тогда ![]() ,
,
![]() ;
;
![]() ;
;![]() ,
,
где ![]() – третьи разделенные разности от функции
– третьи разделенные разности от функции ![]() по точкам t1, t2, t3, t4, tn-3,tn-2, tn-1, tn соответственно.
по точкам t1, t2, t3, t4, tn-3,tn-2, tn-1, tn соответственно.
Тогда ![]() ,
,
![]() .
.
Приведенные системы уравнений решаются методом Гаусса.
Оценка качества восстановленного показателя осуществлялась с помощью нахождения коэффициента расхождения, предложенного Тейлором:
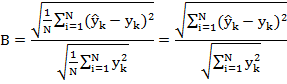
где ![]() – предсказанное значение для yk ; yk – фактическое значение.
– предсказанное значение для yk ; yk – фактическое значение.
2. Сервис выявления тренд-циклической компоненты
Оценка наличия сезонных ритмов во временных рядах осуществлялась на основе функции автокорреляции и её графического представления – коррелограммы. При помощи анализа коррелограммы можно выявить структуру ряда. Если наиболее высоким оказался коэффициент корреляции первого порядка, то исследуемый ряд содержит только тенденцию, если коэффициент автокорреляции порядка h, то ряд содержит циклические колебания с периодичностью в h моментов времени [3].
Последовательность коэффициентов автокорреляции со смещениями 1, 2, 3 и т.д. называют автокорреляционной функцией, значения которой находятся в диапазоне [-1; 1].
Автокорреляционную функцию целесообразно использовать для выделения во временном ряде наличия трендовой и сезонной компонент.
3. Сервис выделения трендов во временных рядах
Выявление наличия неслучайной составляющей сводилось к проверке гипотезы о неизменности среднего значения временного ряда с использованием критерия серий. При его использовании определяется медиана временного ряда, и образуются «серии» из плюсов и минусов по следующему правилу:
![]()
Элементы временного ряда, равные ![]() , в полученной таким образом последовательности не учитываются. Под «серией» понимается последовательность подряд идущих плюсов или подряд идущих минусов. Наличие неслучайной составляющей во временном ряде определяется из условия:
, в полученной таким образом последовательности не учитываются. Под «серией» понимается последовательность подряд идущих плюсов или подряд идущих минусов. Наличие неслучайной составляющей во временном ряде определяется из условия:
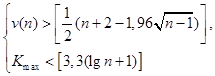 где
где ![]() – общее число серий,
– общее число серий, ![]() – длина наибольшей серии, [ ] – целая часть от числа [1].
– длина наибольшей серии, [ ] – целая часть от числа [1].
Для построения тренда использовались два метода: скользящих средних и экспоненциального сглаживания [4].
Метод скользящих средних заключается в следующем: 1) определяем количество наблюдений, входящих в интервал сглаживания; 2) вычисляем среднее значение наблюдений в интервале сглаживания по формуле:
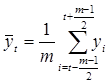 ,
,
где m – количество наблюдений, входящих в интервал сглаживания. И так до тех пор, пока в интервал сглаживания не войдет последнее значение временного ряда.
Альтернативный подход к устранению колебаний в ряде значений состоит в использовании метода экспоненциального сглаживания. Каждое сглаженное значение рассчитывается путем сочетания предыдущего сглаженного значения и текущего значения временного ряда. В этом случае текущее значение временного ряда взвешивается с учётом сглаживающей константы:
![]() ,
,
где St – текущее сглаженное значение;
yt – текущее значение временного ряда;
St-1 – предыдущее сглаженное значение;
α – сглаживающая константа, значение которой варьируется в диапазоне от 0 до 1 [5].
4. Сервис оценки сезонной декомпозиции
Для определения сезонной составляющей разработан алгоритм сезонной декомпозиции.
1. Выделение тренда (метод скользящих средних).
2. Формирование сезонной компоненты (разность между исходным и сглаженным рядом).
3. Вычисление сезонной компоненты (среднее всех значений ряда, соответствующих данной точке сезонного интервала).
4. Определение случайной составляющей.
Информационная система, в состав которой включены данные сервисы, позволяет осуществить комплексный подход к диагностике и прогнозированию состояния здоровья организма человека посредством объединения в единое целое процессов анализа и контроля информации и организации оперативного обмена данными в едином информационном пространстве. Параллельный режим обработки данных обеспечивает высокую загрузку вычислительных ресурсов посредством распределения одной сложной задачи на несколько вычислительных узлов.
Результаты исследования
Экспериментальная выборка составляла 527 объектов исследования. Каждый объект описан вектором состояния ![]() . Исследование проводилось в динамике 23 измерения с периодичностью 1 неделя.
. Исследование проводилось в динамике 23 измерения с периодичностью 1 неделя.
Для успешного решения задачи выявления закономерностей временного изменения показателей биосистемы необходимо выявить и удалить аномальные наблюдения в данных. С этой целью был использован метод Ирвина [2]:
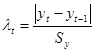 ,
,
где ![]() ,
,
![]() .
.
Для проверки гипотезы о наличии аномальных наблюдений во временном ряде был задан уровень значимости равный 0,05. Если полученное ![]() превышает табличное значение, то элемент
превышает табличное значение, то элемент ![]() считается аномальным наблюдением и заменяется на расчетное значение (среднее из двух соседних значений).
считается аномальным наблюдением и заменяется на расчетное значение (среднее из двух соседних значений).
Полученные после обнаружения аномальных значений временные ряды признаков были проверены на наличие тренда с помощью критерия серий. Как показали исследования, во всех исследованных временных рядах присутствует тренд. Так, например, для показателя «Сосудистый эндотелиальный фактор роста» (VEGF) были получены следующие значения:
медиана равна 12,83, общее количество серий – 3, максимальная длина серии – 5.
При n = 23
![]()
![]() .
.
В данном примере оба неравенства из условия наличия неслучайной составляющей нарушены, что свидетельствует о присутствии во временном ряде неслучайной составляющей.
Для проверки временных рядов на наличие сезонной составляющей использовалась автокорреляционная функция и её графическое представление – коррелограмма. Коррелограмма для признака FEGF представлена на рисунке 1.
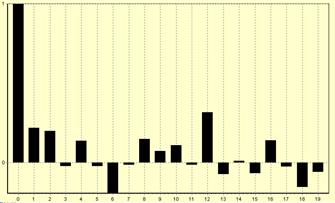
Рис. 1. Показатель VEGF. Период сезонной составляющей – 12
Тренды были построены для тех временных рядов, в которых присутствует сезонная составляющая (по результатам проверки с использованием коррелограммы). В случае, когда для построения тренда был использован метод скользящего среднего, интервал сглаживания для каждого временного ряда был выбран равным периоду сезонных колебаний. При использовании метода экспоненциального сглаживания константа была выбрана равной 0.3. Построенные тренды для признака VEGF представлены на рисунке 2.
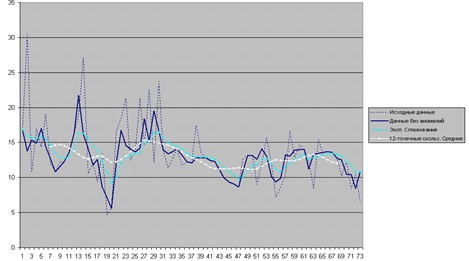
Рис. 2. Тренды для признака VEGF
На основе анализа графического представления временных рядов и их трендов для декомпозиции была выбрана аддитивная модель: X = TC +S + I, где TC – тренд-циклическая компонента, S – сезонная компонента, I – случайная компонента.
Тренд-циклическая компонента получена с помощью метода скользящих средних. Найдены разности между значениями исходного временного ряда и выделенной тренд-циклической компоненты. Вычислена сезонная компонента, как среднее всех значений ряда, соответствующих данной точке сезонного интервала. Получена случайная компонента, как разность значений исходного временного ряда и суммы значений тренд-циклической компоненты и сезонной компоненты. График декомпозиции представлен на рисунке 3.
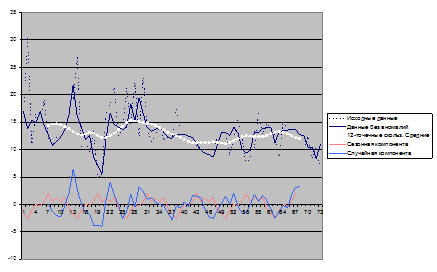
Рис. 3. Декомпозиция временного ряда для признака VEGF
Заключение
Рассмотренные в статье алгоритмы и методы направлены на решение одной из важных проблем: создания эффективных инструментов решения задачи диагностики и прогнозирования состояния здоровья людей. Анализ исследованных временных рядов позволяет представить поведение показателей биохимии крови у здоровых людей.
Апробация информационной медицинской системы на реальных данных показала, что качество решения по вышеизложенному алгоритму удовлетворяет требованиям практического врача. Данная система позволяет выделить данные, в которых присутствует сезонная составляющая, сформировать стандарт поведения исследованных показателей во времени, а также на основе результатов исследования дает возможность оперативно оценить состояние здоровья человека.
Дальнейшие исследования связаны с разработкой магистральных технологий для выявления закономерности реакции организма на условия жизнедеятельности.
Работа выполнена при финансовой поддержке РФФИ, проект № 13-07-90902 мол_ин_нр.
Рецензенты:
Михалев Е.В., д.м.н., профессор, зав. кафедрой педиатрии ФПК и ППС, ГБОУ ВПО «СибГМУ» Минздрава России, г. Томск.
Кочегуров В.А., д.т.н, профессор, ФГБОУ ВПО «Национальный исследовательский Томский политехнический университет», г. Томск.
Библиографическая ссылка
Гергет О.М., Милёшин А.А. ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ ВЫЯВЛЕНИЯ ОСНОВНЫХ ЗАКОНОМЕРНОСТЕЙ ВРЕМЕННОГО ИЗМЕНЕНИЯ ПОКАЗАТЕЛЕЙ БИОСИСТЕМЫ // Современные проблемы науки и образования. – 2013. – № 6. ;URL: https://science-education.ru/ru/article/view?id=10775 (дата обращения: 25.04.2024).



