Введение
В настоящее время большое внимание уделяется исследованию физических свойств материалов, характеризующихся несколькими типами упорядочения (сегнетоэлектрическим, ферромагнитным, упругим и т.п.), т.е. мультиферроиков [5; 7]. Это обусловлено возможностью использования мультиферроиков для создания многофункциональных устройств. Взаимодействие между различными параметрами упорядочений в мультиферроиках может приводить к новым эффектам. Примером таких эффектов является магнитоэлектрический (МЭ) эффект. Композиционные МЭ-мультиферроики, содержащие пьезоэлектрическую и магнитострикционную фазу, обладают гигантским МЭ-эффектом при комнатной температуре, что делает их перспективными для технических применений. В материалах такого рода МЭ-эффект проявляется как результат магнитострикционных и пьезоэлектрических свойств компонентов. Электрическая поляризация индуцируется внешним магнитным полем в присутствии подмагничивающего поля, или индуцированная намагниченность появляется при приложении электрического поля. Количественно МЭ-эффект характеризуется МЭ-коэффициентом по напряжению, αE, равным отношению индуцированного переменного электрического поля к приложенному магнитному переменному полю в условиях разомкнутой электрической цепи. Величина коэффициента определяется параметрами структуры, магнитными, диэлектрическими и механическими параметрами составляющих ее компонентов и частоты магнитного поля [2; 3].
Моделирование МЭ-эффекта в пленочных мультиферроиках обычно основывается на предположении, что пьезоэлектрический и магнитострикционный слои имеют хороший механический контакт. При этом пьезоэлектрический слой ограничивает деформацию магнитного слоя, обусловленную внешним магнитным полем. В несимметричной структуре осевые силы в каждом слое, направленные вдоль длины образца (ось X), создают вращающий момент относительно оси Y, направленной вдоль ширины образца. Таким образом, деформации растяжения-сжатия приводят к изгибным деформациям образца [4; 6].
Задачей данной работы является теоретическое моделирование МЭ-эффекта в слоистых магнитострикционно-пьезоэлектрических структурах с учетом изгибных деформаций. Основные особенности предлагаемой модели заключаются в следующем: (1) учет переменных по толщине образца механических напряжений, электрического и магнитного полей позволяет рассмотреть изгибные деформации образца; (2) получены явные выражения для МЭ-коэффициента по напряжению через материальные параметры компонентов структуры (пьезоэлектрические и пьезомагнитные коэффициенты, коэффициенты жесткости и т.п.) для продольной и поперечной ориентаций электрического и магнитных полей; (3) показано на примерах типичных магнитострикционно-пьезоэлектрических структур, что изгибные деформации вносят существенный вклад в величину МЭ-эффекта.
1. Несимметричная магнитострикционно-пьезоэлектрическая структура
В качестве примера несимметричной слоистой структуры рассмотрим двухслойную структуру, состоящую из магнитострикционного и пьезоэлектрического слоев. В предположении, что толщина слоев мала по сравнению с длиной и шириной слоев, можно использовать теорию изгиба тонких пластин [1].
Для деформаций, электрической и магнитной индукций слоев справедливы следующие уравнения:
pSi = psij pTj + pdki pEk ;
pDk = pdki pTi + pεkn pEn ;
mSi = msij mTj + mqki mHk ; (1)
где pT1, mT1, pS1, mS1 – компоненты тензоров напряжений и деформаций пьезоэлектрической и магнитострикционной фаз, соответственно, pEn – напряженность электрического поля, pDk – электрическая индукция, mHk - напряженность магнитного поля, pdki и mqki – пьезоэлектрический и пьезомагнитный коэффициенты при постоянном механическом напряжении, pεkn – диэлектрическая проницаемость.
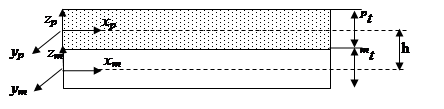
Рисунок 1 – Двухслойная магнитострикционно-пьезоэлектрическая структура. Оси xp и xm направлены вдоль длины образца в срединных плоскостях слоев. pt и mt – толщины пьезоэлектрического и магнитострикционного слоев, h – расстояние между xp и xm
Для учета изгибной деформации, связанной с несимметричностью образца, представим аксиальное смещение в виде линейной функции вертикальной координаты zi: pu1 = pu10 +zp∂w/∂x; mu1 = mu10 +zm∂w/∂x; где iu10 – смещение вдоль оси x при zi =0, w – смещение вдоль z, перпендикулярной плоскости образца, при этом zi отсчитывается от срединной плоскости i-го слоя. Следует отметить, что в общем случае аксиальное смещение можно представить в виде ряда по степеням вертикальной координаты zi. В данной работе рассматривается слабый изгиб и учитывается только линейное по zi слагаемое.
Компоненты деформации связаны со смещением соотношениями: pS1 =∂pu10 /∂x +zp∂2w/∂x2, mS1 =∂mu10/∂x+zm∂2w/∂x2. Очевидно, деформации iS10=∂iu10/∂x удовлетворяют следующему условию: mS10 - pS10 = h/R, где h=(mt + pt)/2, pt, mt – толщины слоев, R - радиус кривизны изогнутого образца. С учетом приведенных выше соотношений выражения для напряжений принимают следующий вид для поперечной ориентации электрического и магнитного полей (поляризация пьезоэлектрика и электрическое поле направлены перпендикулярно плоскости образца, а постоянное и переменное магнитные поля направлены вдоль длины образца):
mT1 =(mS10 + zm/R - mq11 mH1)/ ms11,
pT1 =(mS10 + (zp- h)/R - pd31 pE3 )/ ps11. (2)
Выражение (2) получено в предположении, что ширина слоев мала по сравнению с длиной. Для нахождения деформации mS10 учтем, что суммарная аксиальная сила равна нулю:
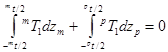 . (3)
. (3)
Подстановка выражений для компонентов напряжений (2) в (3) позволяет получить выражение для mS10.
![]() (4)
(4)
где v= pt/t – объемная доля пьезоэлектрической компоненты, s1=ps11+ms11·pt/mt, t= mt+ pt, и mY, pY – модули Юнга компонент структуры.
Для нахождения радиуса кривизны учтем, что сумма вращающих моментов аксиальных сил каждого слоя должна уравновешиваться результирующим вращающим моментом, индуцируемым в слоях структуры,
![]() (5)
(5)
где 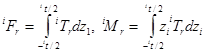 ,
,
Подстановка выражения для mS10 (4), а также выражения для R, полученного из уравнения (5), в (2) позволяет найти компоненты напряжений в слоях структуры. Подстановка найденного выражения для механического напряжения в пьезоэлектрическом слое в условие разомкнутой электрической цепи позволяет вычислить МЭ-коэффициент по напряжению αЕ 31=E3/H1.
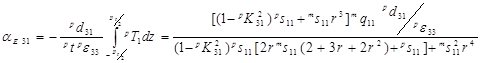 , (6)
, (6)
где ![]() – коэффициент электромеханической связи пьезоэлектрика, r= pt/mt.
– коэффициент электромеханической связи пьезоэлектрика, r= pt/mt.
МЭ-коэффициент по напряжению для продольной ориентации полей αE 33 имеет вид
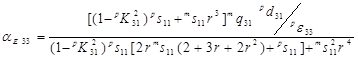 . (7)
. (7)
2. Симметричная магнитострикционно-пьезоэлектрическая структура
При рассмотрении МЭ-эффекта в симметричных структурах суммарный вращающий момент обращается в нуль, при этом радиус кривизны в уравнениях (2) и (4) следует положить равным ∞. Таким образом, вычисление МЭ-коэффициентов сводится в рассмотрению аксиальных деформаций. Моделирование МЭ-эффекта для этого случая рассмотрено в [6]. Выражение для МЭ-коэффициентов по напряжению симметричной магнитострикционно-пьезоэлектрической структуры в одномерном приближении для поперечной ориентации полей можно привести к виду:
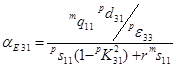 . (8)
. (8)
Для продольной ориентации полей выражение для МЭ-коэффициента по напряжению приобретает вид
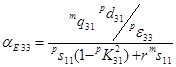 . (9)
. (9)
3. Результаты моделирования для двухслойных структур
Теоретическое моделирование, выполненное выше, позволило получить явные выражения для MЭ-коэффициентов по напряжению для продольной и поперечной ориентаций магнитных и электрических полей. Далее мы применим теорию расчета МЭ-эффекта к слоистой структуре феррит кобальта (ФК) - цирконат-титанат свинца (ЦТС). Так как значение αЕ зависит от объемных долей фаз, МЭ-коэффициент по напряжению был определен как функция отношения толщин пьезоэлектрического и магнитострикционного слоев. Для теоретических оценок использовались следующие параметры компонентов: ps11 =15.3∙10-12 м2/Н, pd31 =-175 пм/В, pε33/ε0=1750, ms11 =6.5∙10-12 м2/Н, mq11 = -188 пм/А, mq31= 56 пм/А, при этом значения пьезомагнитных модулей приведены для частоты измерений 1 кГц.
Результаты расчетов МЭ-коэффициента по напряжению для поперечной ориентации полей с использованием разработанной модели показаны на рис. 2.
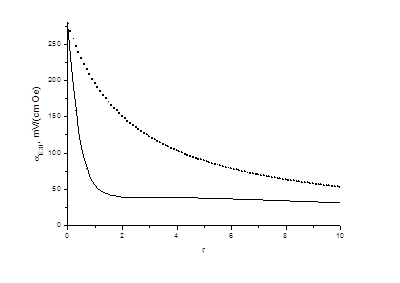
Рисунок 2 – Зависимость МЭ-коэффициента αE 31 для двухслойной (сплошная линия) и симметричной трехслойной (пунктирная линия) структур состава ФК-ЦТС от r = pt/mt
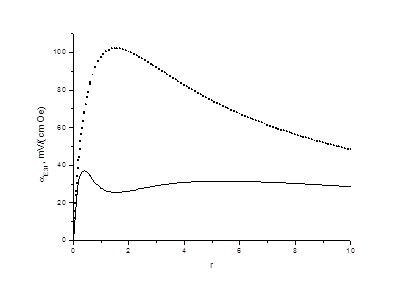
Рисунок 3 – Зависимость МЭ-коэффициента α′Е 31, равного отношению среднего по объему образца электрического поля к внешнему магнитному полю, для двухслойной (сплошная линия) и симметричной трехслойной структур состава ФК-ЦТС r = pt/mt
Рис. 2 показывает, что МЭ-коэффициент по напряжению αЕ принимает наибольшее значение при r → 0. Это связано с тем, что МЭ-коэффициент определен как отношение электрического поля в пьезоэлектрическом слое к внешнему магнитному полю. При этом МЭ-коэффициент α′Е, равный отношению среднего по объему образца электрического поля к внешнему магнитному полю, обращается в нуль при r = 0 (рис. 3). Как следует из рис. 3, МЭ-коэффициент α′Е для двухслойной структуры значительно меньше, чем его величина для симметричной трехслойной структуры для не очень маленьких и не очень больших значений r. Это обусловлено влиянием изгиба двухслойной структуры, которое максимально при приблизительно равных толщинах пьезоэлектрического и магнитострикционного слоев. Величина МЭ коэффициента для двухслойной структуры может быть представлена в виде суперпозиции двух составляющих: (1) вследствие аксиальной деформации растяжения – сжатия и (2) вследствие чистого изгиба. Эти составляющие имеют противоположные знаки и экстремумы при r ≈ 1. В результате график зависимости α′Е от r имеет два максимума и минимум при r ≈ 1 (рис. 3). Сравнение результатов расчета с экспериментальными данными [6] для двухслойной структуры ФК-ЦТС приведено на рис. 4 и 5.
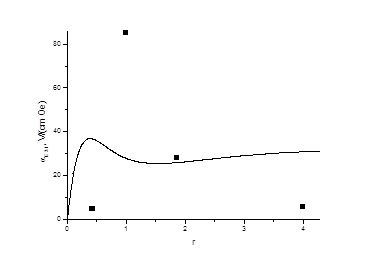
Рисунок 4 - Зависимость МЭ-коэффициента для двухслойной структуры ФК-ЦТС от r = pt/mt для поперечной ориентации полей. Сплошная линия – расчет, точки - эксперимент
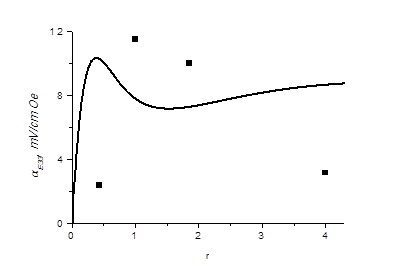
Рисунок 5 - Зависимость МЭ-коэффициента по напряжению для двухслойной структуры состава ФК-ЦТС от отношения толщин слоев r = pt/mt для продольной ориентации магнитных и электрических полей. Сплошная линия – расчет, точки - эксперимент
Рис. 4 и 5 показывают, что результаты моделирования удовлетворительно согласуются с экспериментальными данными.
Заключение
В данной работе рассмотрена точно решаемая модель МЭ-эффекта в симметричных и асимметричных магнитострикционно-пьезоэлектрических структурах. Получены явные выражения для МЭ-коэффициента по напряжению с учетом изгибных деформаций. Показано, что график зависимости МЭ-коэффициента от отношения толщин слоев двухслойной структуры имеет два максимума и минимум при приблизительно равных толщинах магнитострикционной и пьезоэлектрической компонент. Результаты расчетов удовлетворительно согласуются с данными измерений для двухслойных структур на основе феррита кобальта и цирконата-титаната свинца.
Работа выполнена в рамках реализации Федеральной целевой программы «Научные и научно-педагогические кадры инновационной России» на 2009–2013 годы.
Рецензенты:
Захаров А.Ю., д.ф.-м.н., профессор, заведующий секцией кафедры общей и экспериментальной физики ИЭИС «НовГУ», г. Великий Новгород.
Селезнев Б.И., д.т.н., профессор, заведующий кафедрой ФТТМ ИЭИС «НовГУ» г. Великий Новгород.



