Лопастные смесители сыпучих материалов нашли широкое применение в различных отраслях промышленности и сельского хозяйства. Их расчет при проектировании и модернизации существующих конструкций основывается в основном на экспериментальных данных [2; 5]. Целью настоящей работы является построение математической модели смешивания сыпучих материалов на основе теории цепей Маркова [4]. Предыдущие исследования целого ряда авторов [1; 3; 6] показали возможность эффективного использования данного математического аппарата с различным видом цепей (одномерные, двумерные, использующие блочные матрицы и т.д.) для моделирования процесса перемешивания в лопастных смесителях периодического и непрерывного способа действия.
Опираясь на результаты предыдущих исследований, предложена математическая модель, в которой перемещение частиц в процессе смешивания представлено в трёх направлениях:
1) осевом (рис. 1а). Представляет собой перемещение частиц материала между рядами рабочих органов вдоль смесительной камеры;
2) радиальном (рис. 1б). Частицы материала перемещаются в пределах рядов рабочих органов смесителя;
3) окружном (рис. 1в). Перемещение частиц материала происходит по замкнутому циркуляционному контуру.
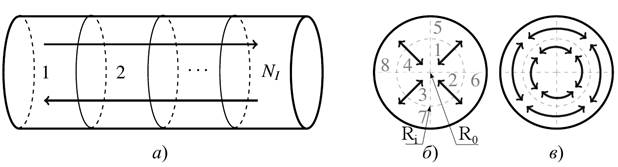
Рисунок 1 – Схема перемещения частиц и разделения на ячейки: (а) – осевое, (б) – радиальное, (в) – окружное.
Смесительная камера разделяется на ячейки равного объёма. В осевом направлении на ![]() одинаковых частей, равных числу рядов рабочих органов (рис. 1а). Нумерацию частей производим от одного торца камеры до другого.
одинаковых частей, равных числу рядов рабочих органов (рис. 1а). Нумерацию частей производим от одного торца камеры до другого.
Каждую часть, полученную при разбиении в осевом направлении, разобьём последовательно в радиальном направлении на ![]() колец (рис. 1б) и в окружном направлении на
колец (рис. 1б) и в окружном направлении на ![]() (рис. 1в) секторов:
(рис. 1в) секторов:
![]() (1)
(1)
где ![]() - угол сектора.
- угол сектора.
Количество ячеек в каждой полученной части определяется формулой:
![]() (2)
(2)
Нумеруются ячейки (рис. 1б) с индексом приращения ![]() где
где ![]() - номер кольца.
- номер кольца.
Радиусы колец (рис. 1б), при условии одинакового объёма ячеек, вычисляются по формуле:
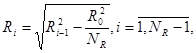 (3)
(3)
где ![]() - радиус смесительной камеры.
- радиус смесительной камеры.
Состояние системы в момент времени ![]() (где
(где ![]() - номер перехода,
- номер перехода, ![]() - длительность перехода), представим в виде вектора-столбца размером
- длительность перехода), представим в виде вектора-столбца размером ![]()
![]() (4)
(4)
Следующее состояние системы ![]() зависит от текущего и может быть представлено в следующей матричной форме:
зависит от текущего и может быть представлено в следующей матричной форме:
![]() (5)
(5)
где ![]() - матрица переходных вероятностей.
- матрица переходных вероятностей.
Матрица переходных вероятностей с учетом трёх направлений перемещения частиц материала определяется по формуле:
![]() (6)
(6)
где ![]() - матрица переходных вероятностей при перемещении частиц в окружном направлении;
- матрица переходных вероятностей при перемещении частиц в окружном направлении; ![]() - матрица переходных вероятностей при перемещении частиц в радиальном направлении;
- матрица переходных вероятностей при перемещении частиц в радиальном направлении; ![]() - матрица переходных вероятностей при перемещении частиц в осевом направлении.
- матрица переходных вероятностей при перемещении частиц в осевом направлении.
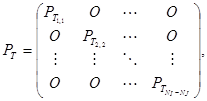 (7)
(7)
где ![]() - нулевая матрица размером
- нулевая матрица размером ![]()
![]() - блочная матрица переходных вероятностей при перемещении частиц в окружном направлении для каждой
- блочная матрица переходных вероятностей при перемещении частиц в окружном направлении для каждой ![]() -й части смесительной камеры при осевом разбиении размером
-й части смесительной камеры при осевом разбиении размером ![]()
![]() .
.
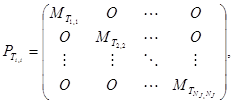 (8)
(8)
где ![]() - нулевая матрица размером
- нулевая матрица размером ![]()
![]() - блочная матрица размером
- блочная матрица размером ![]()
![]() .
.
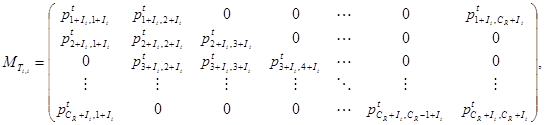 (9)
(9)
где ![]() - вероятность перехода концентрации материала из
- вероятность перехода концентрации материала из ![]() -й ячейки в
-й ячейки в ![]() -ю при окружном смешивании,
-ю при окружном смешивании, ![]()
![]()
![]() - индекс приращения.
- индекс приращения.
Матрица переходных вероятностей при перемещении частиц в радиальном направлении имеет следующий вид:
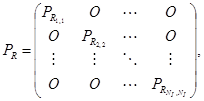 (10)
(10)
где ![]() - нулевая матрица размером
- нулевая матрица размером ![]()
![]() - блочная матрица переходных вероятностей при перемещении частиц в радиальном направлении для каждой
- блочная матрица переходных вероятностей при перемещении частиц в радиальном направлении для каждой ![]() -й части смесительной камеры размером
-й части смесительной камеры размером ![]()
![]() .
.
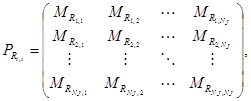 (11)
(11)
где ![]() - блочная матрица размером
- блочная матрица размером ![]()
![]()
![]() :
:
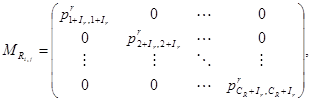 (12)
(12)
где ![]() - вероятность перехода концентрации материала из
- вероятность перехода концентрации материала из ![]() -й ячейки в
-й ячейки в ![]() -ю при перемещении частиц в радиальном направлении,
-ю при перемещении частиц в радиальном направлении, ![]()
![]()
![]() - индекс приращения.
- индекс приращения.
Матрица переходных вероятностей ![]() при перемещении частиц в осевом направлении имеет вид:
при перемещении частиц в осевом направлении имеет вид:
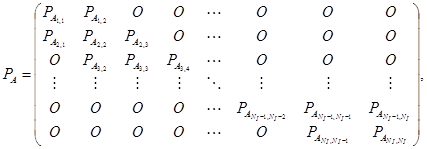 (13)
(13)
где ![]() - нулевая матрица размером
- нулевая матрица размером ![]() , а
, а ![]() - блочная матрица,
- блочная матрица, ![]()
![]() .
.
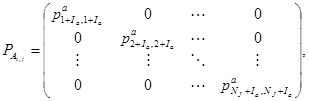 (14)
(14)
где ![]() - вероятность перехода концентрации материала из
- вероятность перехода концентрации материала из ![]() -й ячейки в
-й ячейки в ![]() -ю при перемещении частиц в осевом направлении
-ю при перемещении частиц в осевом направлении ![]()
![]()
![]() и
и ![]() - индексы приращения.
- индексы приращения.
Для двухвальных лопастных смесителей состояние системы можно представить в виде вектора-столбца:
![]() (15)
(15)
где ![]() и
и ![]() - состояния системы при вращении I и II-го валов соответственно (рис. 2), определяемые по формуле (4).
- состояния системы при вращении I и II-го валов соответственно (рис. 2), определяемые по формуле (4).
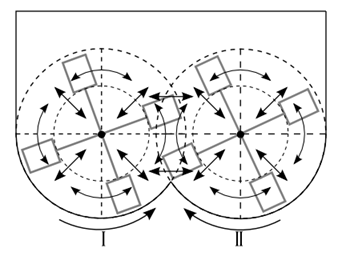
Рисунок 2 – Схема перемещения частиц и разделения на ячейки в двухвальном лопастном смесителе.
Состояние системы ![]() можно представить в матричной форме:
можно представить в матричной форме:
![]() (16)
(16)
где ![]() - матрица смешивания, имеющая вид:
- матрица смешивания, имеющая вид:
![]() , (17)
, (17)
где ![]() - нулевая матрица размером
- нулевая матрица размером ![]() .
.
![]() - матрица обмена частиц материала при вращении I и II-го валов. Элементы матрицы, кроме элементов
- матрица обмена частиц материала при вращении I и II-го валов. Элементы матрицы, кроме элементов ![]() , где
, где ![]() ,
, ![]() ,
, ![]() ,
, ![]() , равны нулю.
, равны нулю.
Идентификация параметров математической модели, в частности вероятности перехода частиц ключевого компонента в осевом (![]() ), радиальном (
), радиальном (![]() ), окружном направлениях (
), окружном направлениях (![]() ) и при обмене частиц при вращении I и II-го вала (
) и при обмене частиц при вращении I и II-го вала (![]() ), определяли, используя результаты экспериментов на лабораторном лопастном смесителе.
), определяли, используя результаты экспериментов на лабораторном лопастном смесителе.
Первоначально загрузку ключевого компонента осуществляли таким образом, чтобы по результатам эксперимента можно было идентифицировать только один параметр. Например, при идентификации вероятности перехода частиц ключевого компонента в осевом направлении загрузку осуществляли в определенный участок по длине смесительной камеры (![]() , рис. 1). При различном времени смешивания определяли концентрации ключевого компонента в каждой ячейке и на основании полученных данных рассчитывали вероятности.
, рис. 1). При различном времени смешивания определяли концентрации ключевого компонента в каждой ячейке и на основании полученных данных рассчитывали вероятности.
Описанная математическая модель позволяет учитывать характерные особенности лопастных смесителей, обеспечивая возможность эффективной модернизации существующих типов и проектирование новых образцов смесительного оборудования.
Рецензенты:
Мизонов В.Е., д.т.н., профессор, заведующий кафедрой прикладной математики ФГБОУ ВПО «Ивановский государственный энергетический университет им. В.И. Ленина», г. Иваново.
Лабутин А.Н., д.т.н., профессор, заведующий кафедрой технической кибернетики и автоматики, ФГБОУ ВПО «Ивановский государственный химико-технологический университет», г. Иваново.



