- Ошибочностью, неоднозначностью, неполнотой и противоречивостью знаний о предметной области и о решаемой задаче.
- Математическая модель в принципе может быть построена, однако ее синтез или изучение связаны с такими затратами, что они существенно превышают выигрыш, приносимый решением.
- В этих задачах «по определению» существует «плохая» исходная информация, характеризующая сложную в семантическом и структурном отношении ситуацию. Экспериментальные данные по существу являются ограниченными, неполными (с пропусками), разнородными, косвенными.
Меру достижения решения слабо формализованной задачи управления и обработки информации будем характеризовать показателем e. При идентификации модели слабо формализованной задачи возникает задача принятия решений в условиях неопределенности: при заданных условиях Z, с учетом неизвестных факторов ξ, найти такую модель G во множестве реализуемых моделей решения слабо формализованной задачи Q (G€Q), которая обеспечивает глобальный экстремум показателя e, соответствующий оптимальному решению задачи. Показатель e зависит от всех трех групп факторов e=ρ(Z, ξ , Q). Однако, как показывает практика, для приемлемого решения слабо формализованной задачи достаточно найти «хороший» локальный экстремум. Поэтому при заданных условиях во множестве реализуемых моделей решения слабо формализованной задачи Q ищутся такие модели GR (GR€Q), которые обеспечивают приемлемое решение задачи, соответствующее приемлемому значению оценки показателя eR= ρ(Z, ξ , GR), где R€{1, ..., T}. Такая задача трудноразрешима классическими методами оптимизации и, как большинство практических задач принятия решений, имеет множество целевых функций, которые не могут быть оптимизированы одновременно из-за присущей им несоразмерности и конфликту между целями. Данная проблема может быть решена посредством компромиссного решения, стремящегося удовлетворить каждую из частных целевых функций. Математически задачу многоцелевого принятия решений можно представить в следующем виде:
e = min [f1(G), f2(G), ..., fk(G)] , (1)
где G € RN и представляет собой атрибуты (структура, параметры) настроенной модели G системы управления и обработки информации.
Задача включает k целей, функции fl(G), 1 ≤ l ≤ k могут быть как линейными, так и нелинейными, и вычисляют критерии eR эффективности моделей системы управления и обработки информации: сложность, робастность, корректность, ошибка модели G (несколько видов в зависимости от задачи моделирования). Для решения задачи (1) был разработан новый нечеткий метод выбора эффективной модели системы управления и обработки информации для многоцелевого принятия решений, на основе комплексных показателей эффективности моделей и нечетких продукционных правил, отражающих предпочтения ЛПР. Метод задает шкалы лингвистических переменных и соответствующих им функций принадлежности, отражающих эффективность моделей при решении задач принятия решений. Метод предусматривает два вида настройки нечеткой системы:
1) по умолчанию: задаются базовые критерии эффективности моделей и нечеткая продукционная модель:
ЕСЛИ e есть (P) и e есть ¬ (N), ТО G есть E, (2)
где e - лингвистическая переменная, отражающая эффективность моделей системы управления и обработки информации относительно критериев eR, которой соответствует два терма: позитивная идеальная модель (P) и негативная идеальная модель (N); G - лингвистическая переменная, отражающая эффективность модели системы управления и обработки информации, которой соответствует функция принадлежности E.
2) вид предусматривает участие ЛПР в процессе настройки разработанного метода и системы продукционных правил (2) путем: выбора количества значений лингвистических переменных e и G, отражающих эффективность моделей, формализации целей fl(G) функционала (1) значениями лингвистических переменных и пополнения ими системы продукционных правил (2).
Опишем первый вид нечеткого метода выбора эффективной модели решения задач управления и обработки информации.
Нечеткая продукционная модель (2) на основе двух лингвистических термов: позитивная идеальная модель (P) и негативная идеальная модель (N) использована для разработки методологии решения задач многоцелевого принятия решений, имеющих неограниченное число альтернатив.
Предложенный метод при решении данного класса задач уменьшает k-мерное пространство целей до двумерного (модель принадлежит классу P и модель не принадлежит классу N), а затем избавляет от несоразмерности между исходными целями. Кроме того, в отличие от многоатрибутного многоцелевое принятие решений всегда рассматривает бесконечное число альтернатив. Исходная задача становится нечеткой двуцелевой задачей программирования [5], и для достижения компромисса при ее решении используется метод выбора эффективной модели системы управления и обработки информации. Это компромиссное решение является решением исходной k-целевой задачи.
Первым шагом в задачах многоцелевого принятия решений, как правило, является определение контрольных точек в многоцелевом пространстве. С учетом этих точек оцениваются альтернативы и принимается компромиссное решение (альтернатива). Для того чтобы математически сформулировать принцип компромисса, сначала определим контрольные точки P и N для формулы (1) как:
f* = {f1*, f2*, ..., fk*}, (3)
f - = {f1-, f2-, ..., fk-}, (4)
где fj*= ![]() fj(G) для Vj € J и fi* =
fj(G) для Vj € J и fi* = ![]() fi(G) для Vi € I; fj-=
fi(G) для Vi € I; fj-= ![]() fj(G) для Vj €J и fi-=
fj(G) для Vj €J и fi-= ![]() fi(G) для Vi € I; fj(G), j € J - цель для максимизации типа «выгода», fi(G), i € I - цель для минимизации типа «стоимость»; k € K, K = I U J. Тогда f* является вектором решения, который состоит из индивидуальных наилучших возможных решений для всех целей и называется P. Аналогично, f - является вектором решения, который состоит из наихудших возможных решений для всех целей и называется N. Заметим, что f* и f - всегда находятся в пределах допустимой области значений формулы (1). Таким образом, лингвистические переменные P и N имеют не только качественное, но и количественное значение, которое используем для определения функции принадлежности на основе вычисленного расстояния до P и N в метрике Миньковского Lp.
fi(G) для Vi € I; fj(G), j € J - цель для максимизации типа «выгода», fi(G), i € I - цель для минимизации типа «стоимость»; k € K, K = I U J. Тогда f* является вектором решения, который состоит из индивидуальных наилучших возможных решений для всех целей и называется P. Аналогично, f - является вектором решения, который состоит из наихудших возможных решений для всех целей и называется N. Заметим, что f* и f - всегда находятся в пределах допустимой области значений формулы (1). Таким образом, лингвистические переменные P и N имеют не только качественное, но и количественное значение, которое используем для определения функции принадлежности на основе вычисленного расстояния до P и N в метрике Миньковского Lp.
Из-за несоразмерности между целями необходимо сначала нормализовать компонентное расстояние для каждой цели (до P и N). Получаем следующие функции расстояния:
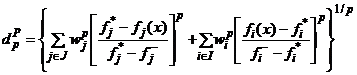 , (5)
, (5)
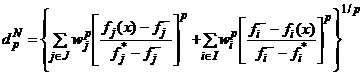 ,(6)
,(6)
где wt, t = 1, 2, ..., k - относительная важность (вес) целей; р = 1, 2, ..., ∞ - параметр функций расстояния; и dpP (уступки) и dpN (поощрения) - расстояния до P и N соответственно.
Из формул (5) и (6) видно, что при увеличении параметра р расстояние уменьшается dp, т.е. d1 > d2 > ... > d∞. Значение р = 1 подразумевает равную важность при формировании функции расстояния d1 для всех индивидуальных отклонений. При р = 2 подразумевается, что наибольшая важность отдается наибольшему отклонению, пропорционально. При р = ∞ наибольшее отклонение полностью доминирует при определении расстояния. d1 (расстояние Манхэттена) и d2 (расстояние Евклида) - наидлиннейшее и наикратчайшее расстояния в геометрическом смысле, a d∞ (расстояние Чебышева) - наикратчайшее в числовом смысле. Среди всех значений р случаи р = 1, 2, ∞ имеют важное практическое значение и являются хорошо известным стандартом в областях теории управления и многоцелевого принятия решений [4].
Лингвистические переменные P и N характеризуются функциями принадлежности соответственно μ1(G) и μ2(G) (рис. 1), которые представляют две невозрастающие (неубывающие) монотонные функции между точками экстремума dp* и dp-, где:
![]() и решение - GP, (7)
и решение - GP, (7)
![]() и решение - GN, (8)
и решение - GN, (8)
![]() , (9)
, (9)
![]() .(10)
.(10)
Основываясь на концепции предпочтения, назначим большую степень там, где короче расстояние до P для μ1(G), и назначим большую степень там, где длиннее расстояние до N для μ2(G).
Определим μ1(G) и μ2(G) как невозрастающую и неубывающую линейные функции, соответственно:
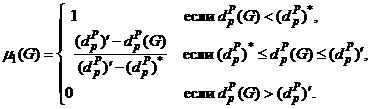 (11)
(11)
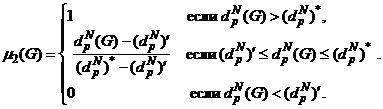 (12)
(12)
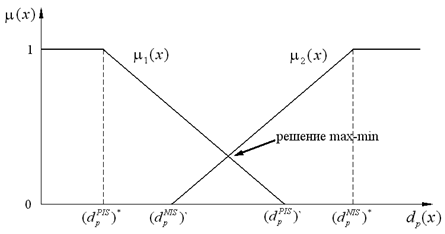
Рис. 1. Функции принадлежности.
Для вычисления значения активации условия (антецедента) нечетких правил (2) с функциями принадлежности (11) и (12) используeтся, в зависимости от реальной задачи: оператор нечеткое «И» или максимума-минимума, предложенный Беллманом и Заде [2]. Значения активации условия (антецедента) нечетких правил (2) агрегируются: оператором нечеткое «И» по следующей формуле:
min[μ1(G), 1-μ2(G)] , (13)
оператором максимума-минимума по формуле:
max{min[μ1(G), μ2(G)]}. (14)
Нечеткий метод выбора эффективной модели системы управления и обработки информации состоит из следующих шагов.
Шаг 1. Задается шкала лингвистической переменной G и соответствующих ей функций принадлежности, отражающих эффективность моделей при решении задач принятия решений. Определяется параметр расстояния р. р = 1, 2 и ∞ стандартные значения в области теории управления.
Шаг 2. Определяется относительная важность wt каждой из k целевых функций формулы (1). Существуют разные методы определения wt, например метод энтропии, также веса может назначить непосредственно ЛПР.
Шаг 3. Определить P (f*) и N (f-) по формулам (3) и (4).
Шаг 4. Найти (dpP)*, (dpN)*, (dpP)′, (dpN)′. Вычислить формулы (7)-(10).
Шаг 5. Найти функции принадлежности m1(G) и m2(G) по формулам (11) и (12).
Шаг 6. Инициализируется система нечетких продукционных правил (2), в которой лингвистические переменные P и N имеют функции принадлежности соответственно μ1(G) и μ2(G).
Шаг 7. Агрегируются значения активации условия (антецедента) нечетких правил (2) оператор нечеткое «И» по формуле (13) или максимума-минимума по формуле (14).
Шаг 8. Выполняется дефаззификация. Механизм нечеткого вывода выбирается в зависимости от особенностей задачи.
Шаг 9. Если решение является удовлетворительным, тогда останов. Однако ЛПР может пожелать изменить значения р, wi и / или функции принадлежности, тогда возврат к шагам 1, 2.
Данная область включает в себя методы принятия решений при многих критериях, ориентирующиеся на задачи с дискретным пространством решений. К настоящему времени разработано большое число методов поддержки принятия решений, учитывающих различные уровни информации о предпочтениях эксперта. Эффективность работы этих методов подтверждается многолетним опытом их применения в различных областях, где встает задача выбора одной альтернативы из ряда предложенных.
Можно констатировать, что в настоящее время для поддержки принятия решений используют различные методы и подходы, которые в совокупности дополняют друг друга. Принятие решений включает выбор последовательности действий и ее реализацию. Поддержка же принятия решений основана на получении многовариантных решений с использованием разных методов.
С целью реализации нечеткого метода выбора эффективной модели системы управления и обработки информации второго вида, который предусматривает участие ЛПР в процессе выбора настроек разработанного метода и системы продукционных правил (2), предложен метод выбора адекватных операторов агрегирования информации (ОАИ) в нечетких иерархических динамических системах. Приведено обобщенное описание метода выбора ОАИ для лингвистической переменной D. Для настройки и дополнения системы продукционных правил вида (2), полагая D = G (или D = е), формируются ОАИ для лингвистической переменной G (или е).
Для определения ОАИ рассмотрим некоторое дерево D с вершинами dj (j = 0, ..., ND). Каждой вершине dj поставим в соответствие множество Xj - множество значений элемента модели проблемы с именем dj. Рассмотрим некоторую не концевую вершину ![]() с подчиненными ей (в смысле рассматриваемого дерева D) вершинами
с подчиненными ей (в смысле рассматриваемого дерева D) вершинами ![]() . Тогда ОАИ
. Тогда ОАИ ![]() есть функция, определенная на множестве всех возможных значений подчиненных вершин и принимающая значения в множестве
есть функция, определенная на множестве всех возможных значений подчиненных вершин и принимающая значения в множестве ![]() :
:
![]()
Так как оценки состояния элементов модели проблемы дает ЛПР, множества Xj (j = 0, ..., ND) представляют собой набор лингвистических значений aj1, aj2, ..., ajNj .
Ясно, что для конкретного элемента модели проблемы число возможных ОАИ является большим: из (15) непосредственно следует, что
![]() .
.
Выбор конкретного оператора ![]() для всех не концевых вершин dj дерева-модели D представляет собой основную проблему настройки системы управления, принятия решений и обработки информации для решения конкретной задачи.
для всех не концевых вершин dj дерева-модели D представляет собой основную проблему настройки системы управления, принятия решений и обработки информации для решения конкретной задачи.
Этот выбор базируется на некоторой информации Ij об «идеальном» ОАИ ![]() . Эта информация представляет собой два множества:
. Эта информация представляет собой два множества:
![]() ,
,
где ![]() - множество высказываний экспертов о «правильном поведении»
- множество высказываний экспертов о «правильном поведении» ![]() ;
;
![]() - множество результатов работы выбранного ОАИ.
- множество результатов работы выбранного ОАИ.
Примерами элементов ![]() могут служить высказывания типа «При
могут служить высказывания типа «При ![]() и
и ![]() и
и ![]() ... и
... и ![]() , значение dj0=aj01», «При сильном возрастании dj1 значение dj0 убывает», «Значение dj0 монотонно изменяется по всем аргументам» и т.п. Множество Ij2 представляет собой таблицу вида табл. 1.
, значение dj0=aj01», «При сильном возрастании dj1 значение dj0 убывает», «Значение dj0 монотонно изменяется по всем аргументам» и т.п. Множество Ij2 представляет собой таблицу вида табл. 1.
Таблица 1

В левом столбце таблицы расположены все попарно различные значения ![]() , в правом - значения dj0, полученные на основе информации Ij (1) (то есть для этих строк
, в правом - значения dj0, полученные на основе информации Ij (1) (то есть для этих строк ![]() =
=![]() ), или значения dj0, полученные в ходе работы с системой, или пустые значения.
), или значения dj0, полученные в ходе работы с системой, или пустые значения.
В начале работы с системой таблица содержит только значения dj0 первого типа (полученные на основе информации Ij (1)). По мере получения и оценки ЛПР информации таблица заполняется на основе вычислений для выбранного оператора ![]() до момента возникновения противоречия - когда ЛПР не согласен с «теоретическим» значением dj0. Если такое противоречие не возникает - значит оператор
до момента возникновения противоречия - когда ЛПР не согласен с «теоретическим» значением dj0. Если такое противоречие не возникает - значит оператор ![]() выбран удачно и является адекватным ОАИ для данного узла дерева-модели. Если противоречие возникает - необходимо повторить процедуру выбора адекватного ОАИ, но на основе дополненной и, быть может, уточненной с ЛПР информации
выбран удачно и является адекватным ОАИ для данного узла дерева-модели. Если противоречие возникает - необходимо повторить процедуру выбора адекватного ОАИ, но на основе дополненной и, быть может, уточненной с ЛПР информации ![]() и
и ![]() . Этот процесс повторяется до тех пор, пока вся таблица не будет заполнена. Адекватный ОАИ для данной вершины dj0- полученная заполненная таблица, которую можно использовать для настройки нечеткой селективной нейросети, разработанной автором [3].
. Этот процесс повторяется до тех пор, пока вся таблица не будет заполнена. Адекватный ОАИ для данной вершины dj0- полученная заполненная таблица, которую можно использовать для настройки нечеткой селективной нейросети, разработанной автором [3].
Модель нечеткой селективной нейросети - гибридный метод на основе нейросетевых, селективных, генетических и нечетких алгоритмов - обеспечивает автоматизированные: структурно-параметрический синтез эффективной модели систем управления, обработки информации и ее корректировку по мере развития реальной системы.
Настроенная нечеткая селективная нейросеть агрегирует информацию в виде нечеткого контроллера специального вида - нечеткого классификатора, представляющего собой нечеткие продукционные правила вида (16).
П: ЕСЛИ X есть A′j , ТО Y есть yj, (16)
где ηj(Y) - функция принадлежности лингвистической переменной yj, ![]() μj (X) - многомерная функция принадлежности (X€Rn) лингвистической переменной A′j, которая представляет собой левый столбец j-той строки таблицы 1.
μj (X) - многомерная функция принадлежности (X€Rn) лингвистической переменной A′j, которая представляет собой левый столбец j-той строки таблицы 1.
Степень неопределенности системы правил вида (16) вычисляется по формуле:
![]() (17)
(17)
где 0<a<1.
Степень неопределенности классификации вычисляется по формуле:
 (18)
(18)
Справедливы следующие утверждения.
Утверждение 1. Если ![]() = 1, то
= 1, то ![]() = 1.
= 1.
Данное утверждение означает, что при максимальной неопределенности системы правил вида (16) неопределенность работы нечеткого классификатора будет также максимальна; она никак не зависит от степени неопределенности входной информации.
Следствие 1. Если ![]() = 0 и
= 0 и
![]()
то ![]() = 0.
= 0.
Следствие утверждает, что при отсутствии неопределенности в (16) и ситуации, когда для любого объекта найдется правило, левой части которого объект полностью удовлетворяет, классификатор будет однозначно классифицировать все объекты (неопределенность классификации будет равна нулю).
Таким образом, равенство нулю степени нечеткости описаний объектов и степени нечеткости системы (16) являются необходимыми условиями равенства нулю степени нечеткости классификации объектов нечетким классификатором.
На основе приведенных утверждений выбор правил вида (16) с наименьшей степенью неопределенности системы правил (17) и классификации (18) гарантирует правильную работу нечеткого метода второго вида для выбора эффективной модели системы управления и обработки информации. Для решения конкретной задачи подбираются соответствующие реализации t-норм и t-конорм.
Разработан нечеткий иерархический метод оценки результатов работы настроенных моделей систем управления и обработки информации, позволяющий выбрать эффективную модель системы управления и обработки информации, учитывающий предпочтения и семантику ЛПР на основе метода выбора ОАИ.
Разработан модуль выбора эффективной модели систем управления и обработки информации, позволяющий учитывать предпочтения и семантику ЛПР, представляющий законченный программный продукт, в состав которого входит ряд программно реализованных методов: нечеткого выбора эффективной модели системы управления, обработки информации для многоцелевого принятия решений и формирования нечеткой селективной нейросети, агрегирующей информацию в виде нечеткого контроллера специального вида - нечеткого классификатора.
Рецензенты:
- Нагрузова Л.П., д.т.н., доцент, профессор кафедры «Строительство» Хакасского технического института - филиала ФГАОУ ВПО «Сибирский федеральный университет», г. Абакан.
- Булакина Е.Н., д.т.н., доцент, профессор кафедры «Автомобили и автомобильное хозяйство» Хакасского технического института - филиала ФГАОУ ВПО «Сибирский федеральный университет», г. Абакан.



