Переработка полезных ископаемых на обогатительных фабриках включает ряд последовательных операций, в результате которых достигается отделение полезных компонентов от примесей. Различия в форме частиц и коэффициенте трения позволяют отделять плоские чешуйчатые частички слюды или волокнистые агрегаты асбеста от частичек породы, которые имеют округлую форму. При движении по наклонной плоскости волокнистые и плоские частички скользят, а округлые скатываются вниз. Сопротивление качению всегда меньше сопротивления скольжению, поэтому плоские и округлые частички движутся по наклонной плоскости с разными скоростями и по разным траекториям, что создаёт условия для их разделения.
В практике обогащения полезных ископаемых нашли применение сепараторы, разделяющие смеси по совокупности таких свойств, как трение и гравитация, удар и трение, гидродинамические и гравитационные свойства, аэродинамические и фрикционные свойства и др. В процессе фрикционной сепарации можно выделить две стадии: первая стадия - движение по поверхности узла стратификации; вторая стадия - свободное падение. Для эффективной работы такого сепаратора обязательными являются два условия: создание потока материала толщиной в одну частицу; разделение сыпучих на составляющие (обеспечение достаточного расстояния между скользящими частицами). Основной задачей первой стадии фрикционной сепарации является сообщение частицам продукта требуемой скорости движения. Задачей второй стадии является собственно разделение - обеспечение падения частиц на разное расстояние.
Разработка и совершенствование узлов стратификации фрикционных сепараторов осуществляются за счет установки нескольких плоскостей под различными углами и на определенном расстоянии друг от друга. Такое расположение позволяет увеличить разницу между скоростями разделения кусков с различными фрикционными и упругими характеристиками, влияя на характер распределения продуктов и траектории движения частиц после схода с полки.
Фрикционные свойства горных пород зависят как от формы отдельных кусков полезного компонента и породы, так и от гранулометрического состава - кусковатости породной массы. Установлено, что нерегулярная форма кусков породы снижает показатели разделения полезного компонента при фрикционной сепарации по сравнению с кусками горной породы идеальной формы.
Степень отклонения формы кусков горных пород от шарообразной можно оценить при помощи критерия «неправильности» (коэффициента формы KФ). Этот критерий в соответствии с работой [1] можно установить по одной из двух методик. Первая из них определяет коэффициент формы как отношение площадей вписанной в образец породы и описанной вокруг него сфер. Если при этом Di - диаметр меньшей из них, а Dе - большей, то соответствующие площади равны: ![]() и
и ![]() . Следовательно,
. Следовательно, ![]() . Таким образом, по первой методике коэффициент формы определяется как отношение квадратов диаметров вписанной и описанной вокруг куска горной породы сфер. Во второй методике используется два линейных размера. Для определения критерия «неправильности» измеряются поперечное и продольное распространение контура образца в прямоугольном шаблоне и коэффициент формы рассчитывается как отношение продольного линейного размера (
. Таким образом, по первой методике коэффициент формы определяется как отношение квадратов диаметров вписанной и описанной вокруг куска горной породы сфер. Во второй методике используется два линейных размера. Для определения критерия «неправильности» измеряются поперечное и продольное распространение контура образца в прямоугольном шаблоне и коэффициент формы рассчитывается как отношение продольного линейного размера (![]() ) к поперечному (Н):
) к поперечному (Н): ![]() .
.
Часто для описания формы куска недостаточно двух измерений. Поэтому используются критерии, основанные на соотношении размеров кусков по трем взаимно перпендикулярным направлениям. Такими величинами являются наибольший размер - длина D, средний размер - ширина S и наименьший размер - толщина H. Для возможности сопоставления данных о кусках разной крупности принято длину и толщину выражать в относительных величинах (относительно ширины): D/S и H/S. Эти отношения называются относительными длиной и толщиной, их принято считать численной характеристикой формы куска. В зависимости от их значения обычно подразделяют куски горной массы на шесть типовых форм [2]:
1) кубообразная ![]() ,
, ![]() ;
;
2) плитчатая ![]() ,
, ![]() ;
;
3) пластинчатая ![]() ,
, ![]() ;
;
4) столбчатая ![]() ,
, ![]() ;
;
5) удлиненно-плитчатая ![]() ,
, ![]() ;
;
6) удлиненно-пластинчатая ![]() ,
, ![]() .
.
Обобщая приведенную классификацию, можно остановиться на трех вариантах: кубообразная форма (1, 2), столбчатая (4) и плитчатая (3, 5, 6).
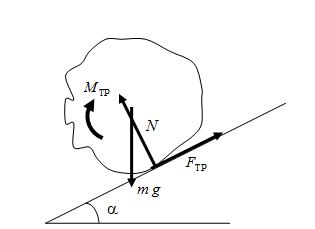
Рассмотрим процесс движения различных типовых форм кусков горных пород по поверхности узла стратификации фрикционного сепаратора. Схема сил, действующих на частицу, приведена на рис. 1. На рисунке обозначены: m g - сила тяжести, а также N, ![]() ,
, ![]() - нормальная реакция, сила трения скольжения и момент трения качения, соответственно.
- нормальная реакция, сила трения скольжения и момент трения качения, соответственно.
|
Рис. 1. Схема сил, действующих на частицу |
![]() , (1)
, (1)
где l- длина полки (наклонной плоскости), м; α - угол ее наклона; f - коэффициент трения скольжения; V0 - скорость частицы в начале участка скольжения, м/с; g - ускорение свободного падения, g=9,8 м/с2.
Движение частицы столбчатой формы зависит от ее ориентации в момент начала движения вдоль полки. За счет момента трения верчения частица за короткий срок стремится занять энергетически рациональное расположение и выходит на режим качения, совершая плоскопараллельное движение.
Приведем вывод выражения для скорости частицы в конце наклонной плоскости при плоскопараллельном движении. Для этого также применяем теорему об изменении кинетической энергии [3]:
![]() ,
,
где T, T0 - кинетическая энергия в конце и в начале участка соответственно; ∑A - сумма работ, приложенных к частице сил.
Кинетическая энергия при плоскопараллельном движении
![]() ,
,
где m - масса частицы, кг; J - ее момент инерции относительно продольной оси, кг.м2.
При этом для качения без скольжения ![]() , а момент инерции относительно продольной оси возможно приближенно представить в виде
, а момент инерции относительно продольной оси возможно приближенно представить в виде ![]() по формуле для однородного цилиндра. Следовательно, кинетическая энергия
по формуле для однородного цилиндра. Следовательно, кинетическая энергия
![]() .
.
Работу при качении частицы по наклонной плоскости совершают сила тяжести и момент сил трения качения (см. рис. 1), поэтому
![]() ,
,
где δ - коэффициент трения качения, м.
Подставляя записанные выражения в уравнение теоремы об изменении кинетической энергии, получим выражение для скорости в виде:
![]() . (2)
. (2)
Для частиц кубообразной формы возможно несколько режимов движения в зависимости от угла наклона полки [4]:
1. Чистое скольжение частицы по наклонной плоскости возникает при условии, что
![]() , (3)
, (3)
где D- условный (эквивалентный) диаметр частицы, м. Скорость частицы в этом случае, как указывалось выше, определяется по формуле (1).
2. Качение без проскальзывания происходит при условии
![]() . (4)
. (4)
Скорость частицы в конце полки можно определить по теореме об изменении кинетической энергии с небольшой корректировкой формулы (2). Дело в том, что кубообразную частицу нельзя приближать формой неправильного цилиндра, а потому ее момент инерции удобнее определять для правильного геометрического тела, близкого по форме к шару, для которого ![]() . Кинетическая энергия в этом случае
. Кинетическая энергия в этом случае
![]() ,
,
работа действующих сил также связана с величиной D:
![]() .
.
Таким образом,
![]() . (5)
. (5)
Учитывая, что при движении без скольжения ![]() , из уравнений плоскопараллельного движения можно получить соотношение между коэффициентами трения в виде:
, из уравнений плоскопараллельного движения можно получить соотношение между коэффициентами трения в виде:
![]() . (6)
. (6)
3) Качение частицы по наклонной плоскости со скольжением происходит при условии
![]() . (7)
. (7)
Поскольку при этом скорость центра тяжести частицы не зависит от ее угловой скорости, то уравнение движения возможно описать по теореме о движении центра масс [2] в соответствии с рис. 1:
![]() , где
, где ![]() .
.
Отсюда видно, что ускорение, а значит и скорость частицы, не зависят от коэффициента трения качения. А это, в свою очередь, означает, что скорость частицы в конце наклонной плоскости также может быть определена, как и при чистом скольжении, то есть по формуле (1).
Начальная скорость V0 во всех полученных формулах может быть получена на основании анализа удара частицы о наклонную плоскость. Так, если загрузка обогащаемого материала происходит с высоты h, то в момент соприкосновения с плоскостью полки скорость частицы ![]() (обозначение для скорости принято нестандартно только для того, чтобы не связывать эту величину с приведенными ранее скоростями).
(обозначение для скорости принято нестандартно только для того, чтобы не связывать эту величину с приведенными ранее скоростями).
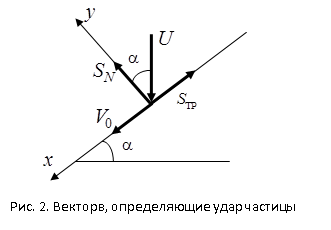
![]() ,
,
где и - составляющие ударного импульса, в проекциях на оси прямоугольной системы координат (рис. 2):
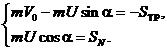
Решая полученную систему алгебраических уравнений и используя гипотезу Рауса ![]() , получим значение скорости в начале движения по наклонной плоскости:
, получим значение скорости в начале движения по наклонной плоскости:
![]() . (8)
. (8)

Как указывалось выше, вторая стадия сепарации - свободный полет частиц обеспечивает их падение на разных расстояниях от места соскальзывания с поверхности полки. Силы сопротивления движению здесь не столь велики, как трение на фрикционной поверхности, особенно при небольших скоростях движения, при которых происходит сепарация. Поэтому на этой стадии движения форма рудных частиц играет не столь заметную роль. Если пренебречь сопротивлением среды, то их свободное движение можно описать с помощью законов равномерного (по горизонтали) и равнопеременного (по вертикали) движений. Для удобства теоретического описания здесь мы вводим прямоугольную систему координат, оси которой направлены горизонтально влево и вертикально вниз (рис. 3). В данной системе координат записываем указанные законы движения в виде:
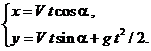
Для y=b из уравнения проекций на ось получаем время падения частицы с высоты b. После подстановки полученного значения в уравнение проекций на ось x определяем дальность полета частицы в виде:
![]() . (9)
. (9)
Приведенные зависимости позволяют описать весь процесс сепарации от стадии загрузки до момента извлечения обогащенного материала. В соответствии с этими соотношениями можно проводить вычислительный эксперимент, в котором нетрудно менять конструктивные параметры фрикционного сепаратора (величины h, l, α).
Наряду с конструктивными параметрами в представленные уравнения входят коэффициенты трения скольжения и качения, которые можно определить только экспериментально. Несмотря на трудности, связанные с исследованием фрикционных характеристик единичных кусков горных пород различной формы, для их определения возможно использовать стандартное лабораторное оборудование. На основании специально разработанных методик [5, 6] установлены экспериментально фрикционные характеристики угля и асбеста для различных материалов узла стратификации. Некоторые из полученных результатов представлены в таблице.
Фрикционные характеристики материалов на различных поверхностях разделения
|
|
Коэффициенты |
||||
|
Продукт |
статического трения |
трения в движении, f |
трения качения, δ |
восстановления, k |
трения при ударе |
|
Асбест |
|
|
-
|
|
|
|
сталь |
0,96 |
0,79 |
- |
0,01 |
0,29 |
|
резина |
1,27 |
0,84 |
- |
0,01 |
0,44 |
|
Порода |
|
|
|
|
|
|
сталь |
0,38-0,53 |
0,23-0,41 |
0,001-0,006 |
0,45-0,48 |
0,08-0,1 |
|
резина |
0,49-0,67 |
0,31-0,49 |
0,001-0,0056 |
0,42-0,52 |
0,08-0,12 |
|
Уголь |
|
|
|
|
|
|
сталь |
0,52 |
0,34 |
0,001-0,0085 |
0,24 |
0,21 |
|
резина |
0,7 |
0,56 |
0,0015-0,0093 |
0,16 |
0,26 |
|
Порода- сланец |
|
|
|
|
|
|
сталь |
0,46 |
0,31 |
- |
0,7 |
0,12 |
|
резина |
0,59 |
0,47 |
- |
0,33 |
0,19 |
|
Глинистое сырье: глина |
|
|
|
|
|
|
сталь |
0,74 |
0,62 |
- |
0,12 |
0,36 |
|
резина |
1,1 |
0,88 |
- |
0,09 |
0,48 |
|
Кварц |
|
|
|
|
|
|
сталь |
0,46 |
0,37 |
0,0008-0,005 |
0,76 |
0,08 |
|
резина |
0,59 |
0,47 |
0,001-0,0055 |
0,33 |
0,12 |
|
Слюда |
|
|
|
|
|
|
сталь |
0,63 |
0,56 |
- |
0,08 |
0,26 |
|
резина |
0,72 |
0,62 |
- |
0,06 |
0,34 |
|
Гранат сталь |
0,45
|
0,32 |
0,0007-0,0048 |
0,45 |
0,12 |
|
резина |
0,56 |
0,42 |
0,001-0,0052 |
0,38 |
0,18 |
Результаты эксперимента свидетельствуют, что статический коэффициент трения по стали меньше, чем по резине для всех представленных в таблице минералов. С точки зрения рассмотрения коэффициента трения как признака разделения руд, наибольший интерес представляет кинетический коэффициент трения, т.к. разделение частиц в основном идет в движении. Кинетический коэффициент трения частиц на 15-35 % меньше статического коэффициента трения. В соответствии с зависимостями [6] проведено экспериментальное определение приведенного коэффициента трения качения горных пород по стальной и резиновой поверхностям. Исследования показывают, что существует закономерная взаимосвязь между крупностью подвижного куска и коэффициентом трения качения: чем больше размер, тем выше коэффициент трения качения и тем больше зависит от модуля упругости минеральных включений. Данная закономерность прослеживается для различных горных пород и поверхностей качения. Различие в коэффициентах трения качения ценного продукта и породы по стали и резине достаточно для их разделения. Полученные данные об упругих свойствах минералов свидетельствуют о высокой контрастности исследуемого признака и возможности его эффективного использования для разделения продуктов различной крупности.
Расчет по вышеприведенным формулам показывает, что для асбестовых, угольных и слюдосодержащих руд при длине полки 1 м и угле наклона 35° горизонтальная дальность полета рудных частиц меняется в пределах 0,6-1,2 м. Разница между дальностью полета полезных минералов и пустой породы составляет 0,3-0,45 м, что доказывает эффективность фрикционного способа разделения данных материалов.
|
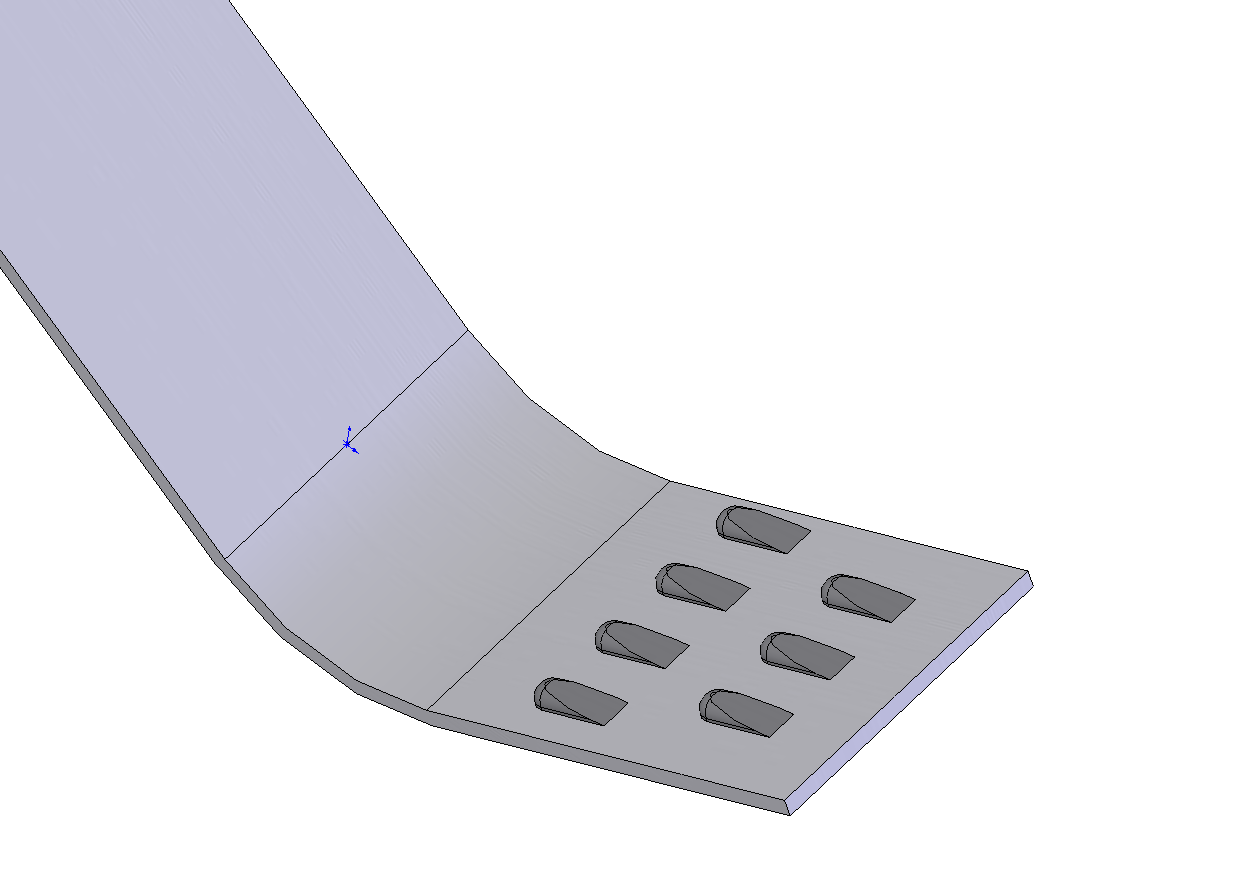
Рис. 4. Узел стратификации с дополнительной зоной сепарации |
Повышения эффективности разделения можно добиться введением дополнительной зоны разделения в узле стратификации в виде плоскости с трамплином и дефлектором (рис. 4). В сепараторах, использующих фрикционные и упругие характеристики разделяемых компонентов, наличие узла стратификации (расслоения) позволяет провести подготовку продуктов к последующему разделению.
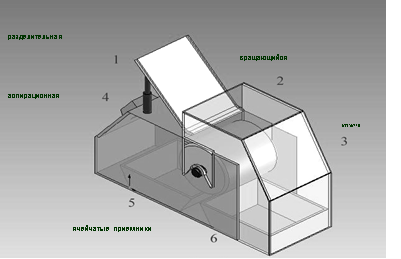
В качестве объекта проектирования была разработана модель сепаратора с подвижной разделительной поверхностью - барабанно-полочный фрикционный сепаратор (БПФС) (рис. 5). Он представляет собой совокупность нескольких механических устройств (полки, барабана), каждое из которых предназначено для разделения горных пород по различным свойствам. На рис.4. представлена модель БПФС, состоящая из разделительной плоскости с трамплином и дефлектором 1 (см. рис. 5), вращающегося барабана 2, аспирационной системы 4, ячейчатых приемников фракции и породы 5,6, весь сепаратор закрыт кожухом 3.
|
Рис. 5. Барабанно-полочный фрикционный сепаратор |
Список литературы
- Адов В.А. Разработка и применение критерия формы для оценки обогатимости угля пневматическим способом / В.А. Адов, В.В. Морозов. - М.: ГИАБ, 2010. - С. 244-250.
- Барон Л.И. Характеристики трения горных пород. - М.: Наука, 1967. - 208 с.
- Никитин Н.Н. Курс теоретической механики. - М.: Наука, 1990 - 324 с.
- Теоретический анализ движения и удара частицы обогащаемого материала о наклонную плоскость / С.А. Ляпцев, В.В. Потапов, В.Я. Потапов [и др.] // Известия вузов, Горный журнал. - 2007. - № 1. - С. 107-110.
- Методика определения упругих и фрикционных характеристик сыпучих материалов / С.А. Ляпцев, В.Я. Потапов [и др.] // Известия вузов, Горный журнал. - 1998. - № 5-6. - С. 105-108.
- Ляпцев С.А. Обоснование методов экспериментального определения коэффициентов трения качения для горных пород» / С.А. Ляпцев, В.Я. Потапов. // Фундаментальные исследования. - М.: РАЕ, 2011. - № 8.
Рецензенты:
- Готлиб Б.М., д.т.н., профессор, зав. кафедрой мехатроники Уральского государственного университета путей сообщения Министерства образования и науки России, г. Екатеринбург;
- Кожушко Г.Г. д.т.н., профессор, зав. кафедрой подъемно-транспортных машин и роботов ФГАОУ ВПО «Уральский федеральный университет имени первого Президента России Б.Н. Ельцина» Министерства образования и науки России, г. Екатеринбург.
Работа получена 07.07.2011.



