Оборудование с параллельными приводами - это класс перспективного технологического оборудования, в конструкции которого используются механизмы с параллельной кинематикой [1]. Наиболее известен из таких механизмов гексапод, часто называемый платформой Стюарта (рис. 1). Механизм образован 6-ю одинаковыми кинематическими цепями, соединяющими выходное звено - платформу с основанием. Физическая реализация такой кинематической цепи - штанга переменной длины. Изменение расстояния между кардановым и сферическим шарнирами в каждой из кинематических цепей посредством винтовой пары (изменение длины штанги) позволяет формировать сложные пространственные перемещения платформы.
Механизм - гексапод и оборудование, построенное на его основе, характеризуются высокой удельной жесткостью и точностью позиционирования выходного звена, однако требует усложненных алгоритмов управления [4]. Помимо задачи перемещения платформы по заданной траектории, алгоритмы управления могут решать задачи повышения производительности оборудования и уменьшения нагрузок на приводы, обеспечивающие перемещение платформы [2, 5]. С практической точки зрения наибольший интерес представляет разработка и реализация управлений, снижающих потребление энергии приводами, т. е. энергоэффективное управление оборудованием с параллельными приводами.
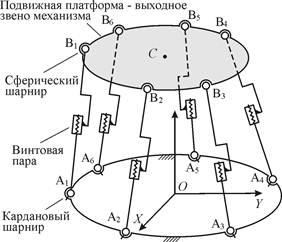
Рис.1. Механизм с параллельной кинематикой - гексапод
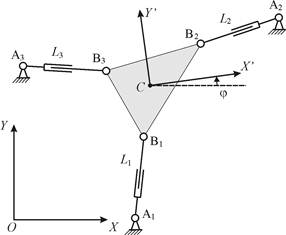
Для иллюстрации подходов к энергоэффективному управлению рассмотрим плоский механизм с параллельной кинематикой - трипод (рис. 2, а). В данном механизме за счет изменения расстояний Lj, j=1...3 между шарнирами в каждой кинематической цепи (изменения длин штанг) обеспечивается плоско-параллельное движение платформы: полюс C перемещается по линейным координатам x и y; поворот платформы вокруг полюса описывается угловой координатой j. Изменение длин штанг осуществляется с помощью приводов.
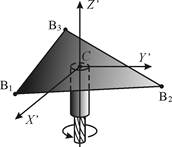
Если на платформе установлен вращающийся инструмент - фреза (рис. 2, б), то появляется возможность реализации технологической операции фрезерования.
|
|
|
|
а) |
б) |
Рис. 2. Плоский трипод (а) и схема установки фрезы на его подвижной платформе (б)
Пусть продольная ось инструмента проходит через полюс C платформы. Тогда для выполнения операции фрезерования необходимо обеспечить перемещение полюса по заданной траектории; угловая координата j для выполнения фрезерования не используется, т. е. является избыточной. Однако наличие этой координаты позволяет придать оборудованию новое качество, обеспечив снижение энергии, потребляемой приводами при фрезеровании.
На рис. 3 показано элементарное перемещение полюса платформы из некоторой точки (xC, yC) траектории в следующую точку (xC*, yC*). Очевидно, что такое перемещение может характеризоваться бесконечным количеством возможных положений платформы механизма в (xC*, yC*). На рис. 3 показаны два возможных положения полюса, переход в каждое из этих положений характеризуется разным изменением длин штанг. Если при переходе в одно из положений (например, в положение I) приводы затратят энергии меньше, чем при переходе в положение II, то можно говорить о повышении энергоэффективности выполнения фрезерования на данном элементарном участке траектории. Так как положения I и II отличаются только значением координаты j, то может ставиться и решаться задача
WΣ(φi)→min,
где WΣ(φ) - суммарное потребление энергии приводами; φi - угловая координата в конце i-го участка траектории. Управление, обеспечивающее минимизацию суммарного потребления энергии приводами, назовем энергоэффективным.
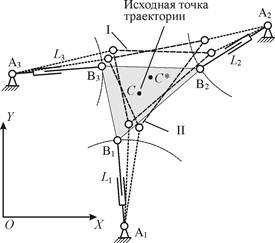
Рис. 3. Варианты перехода платформы трипода на элементарном участке траектории
Энергия Wj, потребляемая приводом каждой из штанг, без учета неизбежных потерь равна по величине работе Aj, совершаемой этим приводом, однако, в отличие от работы, всегда является величиной положительной. Последнее объясняется способностью привода только потреблять энергию от источника; рекуперация энергии приводами технологического оборудования не осуществляется. Таким образом, если на i-м участке траектории длины штанг изменяются на величины ΔLji, а преодолеваемые приводами усилия равны Pji, то потребленная приводами энергия будет равна
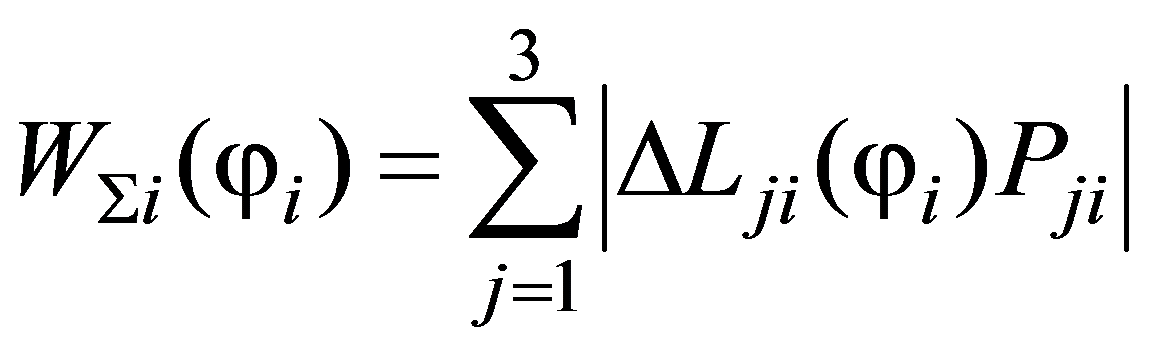 .
.
Преодолеваемые приводами усилия будут определяться внешними силами, действующими на инструмент - силой резания, силой трения и т. п.
Численное моделирование подтвердило возможность уменьшения потребляемой приводами энергии применительно к рассматриваемому плоскому триподу.
Разработанный подход к управлению может быть распространен на оборудование, построенное на основе механизма-гексапода. Такое оборудование в силу большого количества степеней свободы рабочего органа, размещенного на платформе механизма (три линейные и три угловые координаты), может использоваться для многокоординатной обработки сложнопрофильных деталей. При многокоординатной обработке широко используются инструменты со сферической режущей поверхностью - сферические и шаровые фрезы. В этом случае можно говорить об избыточности всех трех угловых координат: траектория движения инструмента задается только линейными координатами центра сферической поверхности. Следовательно, угловые координаты, определяющие ориентацию платформы и инструмента, могут использоваться для построения энергоэффективного управления оборудованием.
Экспериментальные исследования возможности реализации энергоэффективного управления на многокоординатном оборудовании с параллельными приводами проводилось применительно к координатно-измерительной машине КИМ-1000, выпускаемой фирмой «Лапик» (г. Саратов, Россия). Машина построена по гексаподной схеме; особенностью машины является возможность использования ее для обработки материалов методом фрезерования.
В экспериментальной установке обеспечивается нагружение шпинделя, закрепленного на подвижной платформе машины, внешней силой PВнеш. Внешняя сила формируется грузом массой mгр=203 кг, висящем на тросе, и воздействует на эквивалент инструмента, установленный в шпинделе машины.

Рис. 4. Экспериментальная установка на базе координатно-измерительной машины КИМ-1000
В ходе экспериментов реализовывалось движение характерной точки эквивалента инструмента по линейной траектории со скоростью VK=20 мм/с. При этом на 100 мм изменялась только одна линейная координата Y характерной точки эквивалента инструмента; сила PВнеш направлена вдоль этой координаты. Синхронно с движением эквивалента инструмента производилась регистрация энергии, потребляемой приводами машины из электрической сети. Регистрация прекращается по сигналу датчика положения эквивалента инструмента.
Измерительная система координатно-измерительной машины КИМ-1000 оперирует с выходными угловыми координатами, представленными в традиционном для технологического оборудования виде A, B, C. Углы A, B, C соответственно определяют разворот платформы вокруг осей X, Y, Z системы координат, связанной с основанием машины. В серии экспериментов была определена энергия, потребленная приводами на перемещение характерной точки эквивалента инструмента на 100 мм для случая A=B=C=0, т. е. для неразвернутой платформы. Средняя на серии из 15 экспериментов потребленная энергия составила Wэксп = 296,7 Дж.
Рассчитанное с использованием построенных для КИМ-1000 математических моделей потребление энергии приводами для случая A=B=C=0 составило Wпотр = 224,7 Дж, что выше работы AТреб, требуемой для перемещения груза на 100 мм (Атреб =0,1* 203* 9,81 =199,1 Дж ). Следовательно, при реализации энергоэффективного управления можно ожидать снижения потребления приводами энергии на (224,7 - 199,1)/224,7 *100 = 11,4%.
С использованием разработанных автором подходов [3, 6] были рассчитаны значения углов A, B, C, обеспечивающие снижение потребляемой приводами энергии. Графики изменения углов при энергоэффективном управлении показаны на рис. 5 сплошными линиями.
При экспериментальной реализации энергоэффективного управления законы изменения угловых координат были заменены отрезками прямых (пунктирные линии на рис. 5).
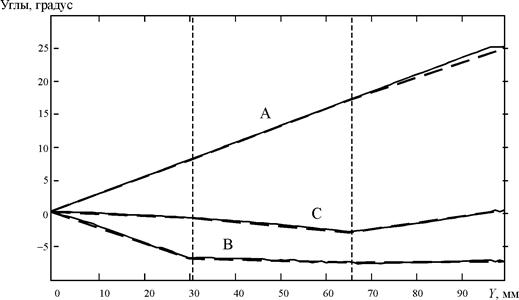
Рис. 5. Изменения выходных угловых координат, обеспечивающие снижение потребляемой приводами энергии
Экспериментальное исследование движения эквивалента инструмента с учетом рассчитанных законов изменения углов показало, что средняя на серии из 15 экспериментов потребленная приводами энергия составила W эфф эксп = 272,7 Дж. Таким образом, обеспечено снижение потребления энергии приводами на 8,1 %, т. е. данное управление является энергоэффективным. Снижение энергии на величину, меньшую ожидаемой, объясняется неизбежными потерями в реальном оборудовании.
Помимо энергоэффективного управления, в нескольких сериях экспериментов реализовывалось движение эквивалента инструмента при произвольных значениях углов A, B, C. Ни в одной из этих серий средняя потребленная приводами энергия не опустилась ниже значения 272,2 Дж.
Таким образом, экспериментально подтверждена возможность снижения потребляемой приводами энергии при выполнении технологической операции многокоординатного фрезерования на оборудовании с параллельными приводами за счет рационального управления. Возможность снижения затрат энергии даст оборудованию с параллельными приводами дополнительные конкурентные преимущества.
Список литературы
- Обрабатывающее оборудование нового поколения. Концепция проектирования / В.Л. Афонин, А.Ф. Крайнов, В.Е. Ковалев и др.; под ред. В.Л. Афонина. - М.: Машиностроение, 2001. - 256 с.
- Смирнов В.А. Избыточность координат как фактор возможности оптимального управления оборудованием с параллельными приводами // Информационные технологии моделирования и управления. Научно-технический журнал. - Воронеж: Научная книга. - 2010. - № 1(60). - С. 126-131.
- Смирнов В.А. Кинетостатическое моделирование энергоэффективного управления оборудованием с параллельной кинематикой / В.А Смирнов // Вестник ЮУрГУ. Серия «Машиностроение». - 2010. - Вып. 16. №29 (205). - С. 65-70.
- Смирнов В.А. Научные основы и алгоритмы управления оборудованием с параллельными приводами / В.А. Смирнов. - Челябинск: Издательский центр ЮУрГУ, 2009. - 164 с.
- Смирнов В.А. Повышение производительности обработки на оборудовании с параллельной кинематикой / В.А Смирнов // Вестник ЮУрГУ. Серия «Машиностроение». - 2010. - Вып. 15. №10 (186). - С. 72-76.
- Смирнов В.А., Сюськина Ю.Л. Повышение энергоэффективности оборудования с параллельными приводами / В.А. Смирнов, Ю.Л. Сюськина // Современные проблемы информатизации в анализе и синтезе программных и телекоммуникационных систем: сб. трудов; вып. 15 (по итогам XV международной открытой научной конференции) / под ред. д.т.н., проф. О.Я. Кравца. - Воронеж: Научная книга, 2010. - С. 383-387.
Рецензенты:
- Кулешов В.В., д.т.н., профессор, зав. кафедрой «Детали машин» ФГОУ ВПО «Челябинская государственная агроинженерная академия», г. Челябинск.
- Ерофеев В.В., д.т.н., профессор, зав. кафедрой «Технологии и организации технического сервиса» ФГОУ ВПО «Челябинская государственная агроинженерная академия», г. Челябинск.
Работа получена 07.07.2011.