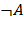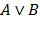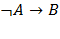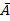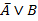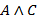Предмет «Математическая логика» является одной из ведущих дисциплин математического цикла, способствующей формированию логического мышления и приемов дедуктивных рассуждений, необходимых для эффективного усвоения других предметов. Действительно, умение мыслить последовательно, проводить правдоподобные рассуждения, выдвигать гипотезы, приводить опровержения неправильных выводов не приходит само по себе, а требует целенаправленного формирования. Изучая математическую логику, студенты, по сути, знакомятся с современным математическим языком, являющимся, как известно, языком любой науки.
Материалы и методы исследования. Методы исследования носили комплексный характер, среди них выделялись теоретические методы: анализ научно-методических статей и учебных пособий, анализ учебников и задачников по математической логике и эмпирические методы: анкетирование студентов и преподавателей, наблюдение за процессом составления и решения задач студентами, а также педагогический эксперимент.
Проведенный анализ показал, что существует ряд исследований, посвященных обучению решению и составлению школьных математических задач (Ю.М. Колягин, Г.И. Саранцев, Е.С. Канин, Р.Г. Хазанкин, П.М. Эрдниев и др.), однако практически нет методических работ, посвященных обучению студентов составлению задач по различным разделам математики, в том числе математической логики.
Дисциплина «Математическая логика» включает в себя такие разделы, как алгебра высказываний, исчисление высказываний, логика предикатов и их исчисления, решение логических задач. Программа курса соответствует требованиям ФГОС ВО. Особенностью дисциплины «Математическая логика» на нашем факультете является не только формирование представлений об основах математической логики и способности применять полученные теоретические знания к решению актуальных прикладных задач, но и самостоятельное составление студентами под руководством преподавателя заданий по основным разделам курса.
Цель исследования: разработка методических приемов по обучению студентов конструированию задач по основным разделам математической логики.
В организации процесса составления задач можно выделить следующие этапы:
1) повторение пройденного теоретического материала (основных операций и законов алгебры логики);
2) решение задач математической логики;
3) самостоятельное составление аналогичных задач;
4) решение сконструированных задач на практических занятиях;
5) проверка ответа и хода решения;
6) отбор сконструированных (либо обобщенных на их основе) заданий для банка задач раздела.
При конструировании собственных задач обучающемуся приходится анализировать пройденный теоретический материал, находить в нем главное, рассматривать характеристические свойства объектов, выделять возможные типы задач в рассматриваемом разделе и способы их решения. Самостоятельное составление задач иногда вызывает трудности у студентов, поскольку требует от них осознанного применения необходимого математического материала. В то же время такая работа способствует формированию у студентов инициативы, критического мышления, самостоятельности, творческого подхода, повышает их интерес к учебе. Действительно, как отмечают многие методисты [1–3], самостоятельно составленная задача запомнится намного глубже и прочнее, чем просто решенная. Психологически сконструированную самим задачу чаще легче решить, чем готовую задачу. Кроме того, только тот человек, который научится выделять проблемы, сможет эффективно их решать. Ведь конструирование задач часто требует проведения рассуждений, которые при решении готовых задач не всегда выполняются.
Говоря о методике составления математических задач, необходимо ответить на два важных вопроса:
1. Зачем учить составлять задачи?
2. Как составлять задачи?
Ответы на эти вопросы нами даны в статье «Составление и решение практических задач на построение» [4]. Поэтому не будем подробно останавливаться на этих серьезных вопросах, а сразу перейдем к практическому решению проблемы – составлению задач по математической логике.
Рассмотрим конструирование обучающимися задач из раздела «Алгебра высказываний» на практических занятиях с учетом выделенных выше этапов.
Первый этап предполагает актуализацию знаний по изученному разделу [5–7]. В ходе практических занятий студенты выделяют:
1) основные математические понятия раздела: логика, формальная логика, математическая логика, высказывания, алгебра высказываний, таблица истинности и др.;
2) основные операции: отрицание, конъюнкция, дизъюнкция, импликация, эквиваленция и др.;
3) основные законы математической логики: закон тождества, закон противоречия, закон исключенного третьего, закон двойного отрицания, коммутативный, ассоциативный и дистрибутивный законы, закон идемпотентности, закон поглощения и др.
На втором этапе в ходе решения задач по рассматриваемому разделу обучающиеся выявляют основные типы задач и способы их решения. В результате такой работы были выделены основные виды заданий: построить таблицу истинности для предложенной формулы; доказать тождество; упростить формулу; вычислить значение функции на конкретном числовом наборе; решить логическое уравнение; найти СДНФ и СКНФ формулы разными способами; зная СКНФ (либо СДНФ), найти первоначальный, более простой вид формулы.
Третий этап был посвящен самостоятельному составлению студентами задач, аналогичных рассмотренным на занятии. Просто применяя аналогию, получаем задачу, подобную исходной. При этом при конструировании задач по аналогии иногда случается, что формально полученный ответ не имеет смысла. Поэтому обучающиеся обязательно должны проверять ответы, найденные при решении сконструированных ими задач. Мы согласны с Е.С. Каниным [8], что составление таких задач помогает учащимся лучше понять структуру математических задач, т.е. существенно углубляет и расширяет математические представления и знания учащихся.
Приведем примеры задач, сконструированных обучающимися самостоятельно.
Задача № 1. Построить таблицу истинности для логической формулы:
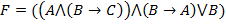
|
A |
B |
C |
1 |
2 |
3 |
4 |
5 |
6 |
F |
|
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
|
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
|
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
|
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
|
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
|
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
Задача № 2. Доказать логическое тождество: 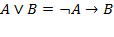 .
.
Решение: Построив таблицу истинности, убеждаемся, что данное равенство является тождеством.
|
A |
B |
|
|
|
|
0 |
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
1 |
Задача № 3. Доказать, что следующая логическая формула является тавтологией:
(X ® Y) Ú (Y ® X).
Решение: Построив таблицу истинности, убеждаемся, что данная формула является тавтологией.
|
X |
Y |
X→Y |
Y→X |
(X→Y)∨(Y→X) |
|
0 |
0 |
1 |
1 |
1 |
|
0 |
1 |
1 |
0 |
1 |
|
1 |
0 |
0 |
1 |
1 |
|
1 |
1 |
1 |
1 |
1 |
Задача № 4. Упростить логические формулы: 1)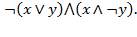
Решение: 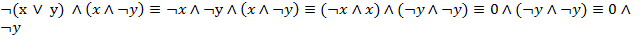 =0.
=0.
2) ¬ (x ∨ y) ∧ ¬ (z ∧ y) ∨ x.
Решение: ¬ (x ∨ y) ∧ ¬ (z ∧ y) ∨ x ≡ ¬ x ∧ ¬ y ∧ (¬ z ∨ ¬ y) ∨ x ≡ (¬ x ∧ ¬ y) ∨ x ≡ (¬ x ∨ x) ∧ (x ∨ ¬ y) ≡ 1 ∧ (x ∨ ¬ y) ≡ x ∨ ¬ y.
3) x ∧ y ⇔ x.
Решение: x ∧ y ⇔ x ≡ (x ∧ y ∧ x) ∨ (¬ (x ∧ y) ∧ ¬ x) ≡ (x ∧ y) ∨ ((¬ x ∧ ¬ y) ∧ ¬ x) ≡ (x ∧ y) ∨ ¬ x ≡ (¬ x ∨ x) ∧ (¬ x ∨ y) ≡ 1 ∧ (¬ x ∨ y) ≡ ¬ x ∨ y.
4) x ⊕ x ∨ y.
Решение: x ⊕ x ∨ y ≡ (x ∧ ¬ (x ∨ y) ∨ (¬ x ∧ (x ∨ y))) ≡ (x ∧ ¬ x ∧ ¬ y) ∨ ((¬ x ∧ x) ∨ (¬ x ∧ y)) ≡ (0 ∧ ¬ y) ∨ (0 ∨ (¬ x ∧ y)) ≡ 0 ∨ (¬ x ∧ y) ≡ ¬ x ∧ y.
Задача № 5. Вычислить значение функции на наборе (0,1,0):
1) 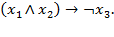 Ответ: 1.
Ответ: 1.
2) 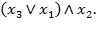 Ответ: 0.
Ответ: 0.
3) 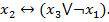 Ответ: 1.
Ответ: 1.
В ходе составления задач на вычисление значений формулы некоторые студенты проявили творчество и предложили задание «Отгадать зашифрованное слово».
Задача № 6. Расшифровать слово, выбрав буквы, которые соответствуют истинностным формулам при a = 1, b = 1, c = 0:
1) ¬ (a ∧ b) ⇔ c ∨ a – Б
2) a ⊕ c → ¬ (b ∧ a) – В
3) a → (¬ c ∧ ¬ b) ∨ a – А
4) с ⊕ b ⇔ ¬ a – П
5) (b ∨ ¬ a ∧ c) ⇔ b ⊕ c ∧ b – Л
6) ¬ (a ∧ b ∨ c) ⊕ a ∨ b ∧ c – Г
7) ¬ (a ∧ b ∧ c) → ¬ (a ∨ b ∨ c) – Е
8) a ⇔ b ⊕ c – О
9) (a → b) ⇔ ¬ (a ∨ c) – Н
10) c ∧ a ⇔ ¬ (b ∨ c) – Р
11) (c → b) ⊕ (a → c) – И
12) ¬ c ∨ b ∧ a → c – С
13) ¬ (a ∨ b) ∨ c ⊕ c – К
14) c ∨ b → a ∨ b ∧ c – Т
15) ¬ (a ∨ b) ∨ c ⇔ a ∨ c – Х
16) a ⇔ a ∨ ¬ (b ∧ c) – М
Ответ: слово «алгоритм».
Задача № 7. Решить логическое уравнение: 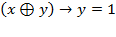 .
.
Решение. Решим уравнение, используя таблицу истинности логических операций.
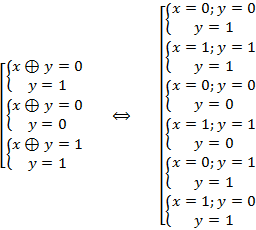
Ответ: (1;1), (0;0), (0;1).
Задача № 8. Следующую логическую формулу привести к СДНФ, предварительно приведя ее равносильными преобразованиями к ДНФ: A ≡ a(bc→ab).
A ≡ a(bc→ab).
Решение: A ≡ a(bc→ab) ≡ a(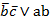 ) ≡ a(
) ≡ a(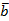 ∨
∨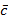 ∨ab) ≡ a
∨ab) ≡ a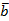 ∨a
∨a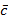 ∨ab ≡ ДНФA.
∨ab ≡ ДНФA.
a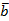 (c∨
(c∨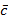 )∨a
)∨a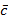 (b∨
(b∨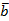 )∨ab(c∨
)∨ab(c∨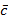 ) ≡ a
) ≡ a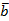 c∨a
c∨a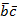 ∨ab
∨ab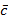 ∨a
∨a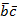 ∨abc∨ab
∨abc∨ab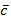 ≡ a
≡ a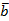 c∨a
c∨a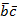 ∨ab
∨ab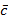 ∨abc ≡ СДНФA.
∨abc ≡ СДНФA.
Ответ: СДНФA ≡ a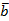 c∨a
c∨a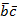 ∨ab
∨ab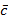 ∨abc.
∨abc.
Задача № 9. Привести следующие формулы к СДНФ с помощью равносильных преобразований:
1. 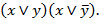
Решение: (x∨y)(x∨y¯ ) ≡ x≡ x(y∨y¯) ≡ xy∨xy¯.
2. x(y¯∨z).
Решение: 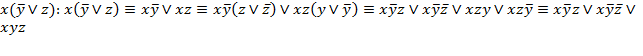 .
.
Задача № 10. Для логической формулы A ≡ a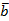 ∨a
∨a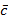 ∨ab найти СКНФ путем равносильных преобразований, предварительно приведя ее к КНФ.
∨ab найти СКНФ путем равносильных преобразований, предварительно приведя ее к КНФ.
Решение: A ≡ a(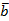 ∨
∨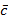 ∨b) ≡ a∧1 ≡ a ≡ КНФA.
∨b) ≡ a∧1 ≡ a ≡ КНФA.
A ≡ a∨(b∧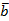 ) ≡ (a∨b)∧(a∨
) ≡ (a∨b)∧(a∨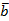 ) ≡ ((a∨b)∨c∧
) ≡ ((a∨b)∨c∧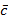 )∧((a∨
)∧((a∨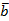 )∨c∧
)∨c∧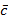 ) ≡
) ≡
≡ (a∨b∨c)∧(a∨b∨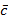 )∧(a∨
)∧(a∨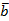 ∨c)∧(a∨
∨c)∧(a∨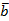 ∨
∨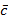 ) ≡ СКНФA.
) ≡ СКНФA.
Ответ: СКНФA ≡ (a∨b∨c)∧(a∨b∨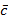 )∧(a∨
)∧(a∨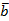 ∨c)∧(a∨
∨c)∧(a∨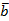 ∨
∨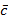 ).
).
Задача № 11. Привести следующую формулу к СКНФ с помощью равносильных преобразований: 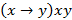 .
.
Решение: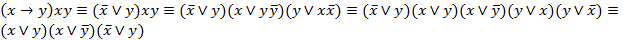 .
.
Задача № 12. Выяснить, является ли следующая формула выполнимой:
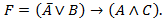
|
A |
B |
C |
|
|
|
F |
|
0 |
0 |
0 |
1 |
1 |
0 |
0 |
|
0 |
0 |
1 |
1 |
1 |
0 |
0 |
|
0 |
1 |
0 |
1 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
1 |
0 |
0 |
|
1 |
0 |
0 |
0 |
0 |
0 |
1 |
|
1 |
0 |
1 |
0 |
0 |
1 |
1 |
|
1 |
1 |
0 |
0 |
1 |
0 |
0 |
|
1 |
1 |
1 |
0 |
1 |
1 |
1 |
Ответ: формула выполнима.
Задача № 13. С помощью равносильных преобразований упростить логическую формулу: 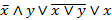 .
.
Решение: 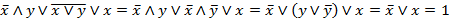 .
.
На четвертом и пятом этапах студенты с интересом решали сконструированные их одногруппниками задачи, бурно обсуждали разные способы решения, иногда находили и исправляли ошибки в предлагаемых задачах.
На шестом этапе особенно понравившиеся задачи после совместного обсуждения добавлялись в банк задач данного раздела. В дальнейшем задания из этого банка задач могли использоваться для контроля знаний обучающихся.
Результаты исследования и их обсуждение. В ходе проведенного исследования совместно со студентами был разработан банк задач по математической логике, используемый в дальнейшем для обучения и контроля знаний. Разработанные авторами статьи методические приемы по обучению студентов конструированию задач по основным разделам математической логики направлены на формирование соответствующих компетенций, на воспитание самостоятельности, формирование критичности и творческого потенциала. Владение приемами конструирования и решения задач позволит эффективно подготовить студентов к их к будущей педагогической деятельности. И такая работа регулярно проводится на нашем факультете на практических занятиях по методическим дисциплинам [3, 4], при выполнении заданий во время прохождения педагогической практики, при организации и руководстве научно-исследовательской деятельностью студентов [9], а также при подготовке студентами научно-методических комплексов [10].
Выводы. Анализ проделанной работы показал, что самостоятельное конструирование задач позволяет лучше усвоить тему, выработать умения и навыки решения основных задач раздела, понять структуру задач математической логики, расширить математические представления и знания обучающихся, сформировать приемы исследовательской работы, развить творческий потенциал обучающихся. В процессе решения предложенных одногруппниками задач студенты исправляют решения задач, находят ошибки в ответах, корректируют условия заданий. Все это способствует формированию их критического мышления. Таким образом, проделанная работа, на наш взгляд, будет очень полезна для студентов педагогического образования, поскольку их будущая профессиональная деятельность связана с обучением учащихся решению математических задач.