Стабилизация неустойчивой и хаотической динамики является важной частью общей задачи управления динамическими системами. Значительное продвижение в этой области связано с результатами, полученными в интенсивно развивающейся области – управлении хаосом [1-4].
В настоящей работе возможности оптимальной параметрической коррекции изучены на семействе диссипативных неавтономных систем, описываемых дифференциальным уравнением вида:
![]() ,
, ![]() (1)
(1)
где ![]() – потенциал, определяющий собственную динамику системы,
– потенциал, определяющий собственную динамику системы, ![]() – гармоническое параметрическое возмущение амплитуды
– гармоническое параметрическое возмущение амплитуды ![]() и частоты
и частоты ![]() ,
, ![]() – диссипация. Система (1) описывает параметрически возбуждаемый диссипативный колебательный контур. Вариативность модели связана с видом потенциала, а также показателем степени переменной
– диссипация. Система (1) описывает параметрически возбуждаемый диссипативный колебательный контур. Вариативность модели связана с видом потенциала, а также показателем степени переменной ![]() в
в ![]() .
.
Рассмотрим случай ![]() , тогда (1) примет вид:
, тогда (1) примет вид:
![]() , (2)
, (2)
где ![]() – собственная частота колебаний системы без параметрического возмущения. При выполнении условий резонанса
– собственная частота колебаний системы без параметрического возмущения. При выполнении условий резонанса ![]() , где
, где ![]() – порядок резонанса, возникает параметрическая неустойчивость, приводящая к экспоненциальному нарастанию амплитуды колебаний. Линейное затухание
– порядок резонанса, возникает параметрическая неустойчивость, приводящая к экспоненциальному нарастанию амплитуды колебаний. Линейное затухание ![]() не стабилизирует параметрическую неустойчивость. Полагая в (2)
не стабилизирует параметрическую неустойчивость. Полагая в (2) ![]() , приходим к известному в теории параметрических колебаний уравнению Матье [2]:
, приходим к известному в теории параметрических колебаний уравнению Матье [2]:
![]() . (3)
. (3)
На рис. 1(а),(b) для случая основного параметрического резонанса ![]() представлено развитие неустойчивого динамического режима системы (3). Видно, что колебания неограниченно нарастают.
представлено развитие неустойчивого динамического режима системы (3). Видно, что колебания неограниченно нарастают.
Положим ![]() и введем в (3) корректирующую функцию
и введем в (3) корректирующую функцию ![]() :
:
![]() . (4)
. (4)
Функция ![]() играет роль управления. Введем фазовое ограничение в виде круга
играет роль управления. Введем фазовое ограничение в виде круга
![]() (5)
(5)
и построим штрафную функцию ![]() за его нарушение, где
за его нарушение, где ![]() – штрафной параметр.
– штрафной параметр.
Задача оптимального управления имеет вид: требуется удержать систему (4) внутри допустимого множества (5) с наименьшими затратами энергии 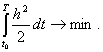
Составим функцию Гамильтона:
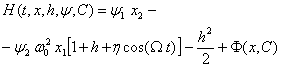 ,
,
где ![]() ,
, ![]() – сопряжённые переменные. Из необходимого условия оптимальности
– сопряжённые переменные. Из необходимого условия оптимальности ![]() найдем оптимальную корректирующую функцию:
найдем оптимальную корректирующую функцию:
![]() . (6)
. (6)
Оптимальная траектория ![]() находится интегрированием следующей системы уравнений и подбором
находится интегрированием следующей системы уравнений и подбором ![]() :
:
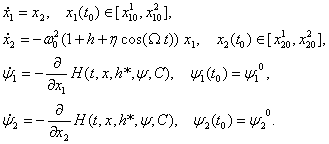
где ![]() – вектор начальных условий для сопряжённой системы, ортогональный вектору
– вектор начальных условий для сопряжённой системы, ортогональный вектору ![]() .
.
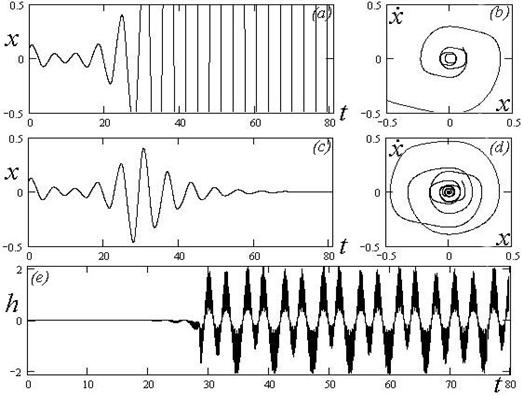
Рисунок 1. Коррекция уравнения Матье (3), ![]() ,
, ![]() ,
, ![]() :
:
(a), (b) – неустойчивый режим до коррекции,
(c),(d) – фазовая плоскость режима коррекции,
(e) – график оптимальной корректирующей функции.
На рис. 1(с),(d) представлены результаты численного моделирования уравнения (3) в условиях основного параметрического резонанса. Они получены с фазовым ограничением (5) при ![]() ,
, ![]() и параметром штрафа
и параметром штрафа ![]() . Оптимальная параметрическая коррекция позволила стабилизировать неустойчивую систему в состоянии равновесия. При соответствующих значениях
. Оптимальная параметрическая коррекция позволила стабилизировать неустойчивую систему в состоянии равновесия. При соответствующих значениях ![]() стабилизация имеет место для начальных условий, лежащих внутри допустимого множества. Результаты аналогичны и при соотношении частот
стабилизация имеет место для начальных условий, лежащих внутри допустимого множества. Результаты аналогичны и при соотношении частот ![]() .
.
График корректирующей функции ![]() на рис. 1(e) позволяет увидеть особенности коррекции. Вначале фазовая траектория системы находилась внутри фазового ограничения (несколько обходов вокруг начала координат). При этом
на рис. 1(e) позволяет увидеть особенности коррекции. Вначале фазовая траектория системы находилась внутри фазового ограничения (несколько обходов вокруг начала координат). При этом ![]() . Всплеск корректирующего воздействия обусловлен тем, что параметрическая неустойчивость начала выталкивать траекторию за область круга. В результате включился алгоритм учета фазовых ограничений, и система стабилизировалась в нуле.
. Всплеск корректирующего воздействия обусловлен тем, что параметрическая неустойчивость начала выталкивать траекторию за область круга. В результате включился алгоритм учета фазовых ограничений, и система стабилизировалась в нуле.
Рассматривалась также общая скорректированная система вида
![]() . (7)
. (7)
На рис. 2 представлен результат общей коррекции с фазовым ограничением в виде единичного круга и параметром штрафа ![]() .
.
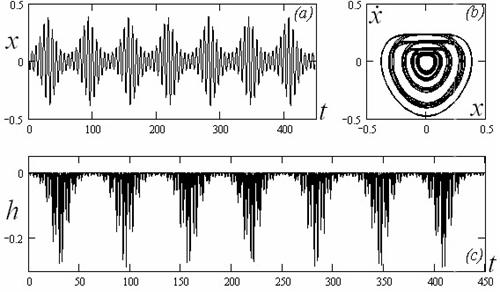
Рисунок 2. Общая параметрическая коррекция параметрически возмущенного уравнения Матье (7), ![]() ,
, ![]() ,
, ![]() :
:
(a) – зависимость координаты от времени,
(b) – фазовая плоскость режима коррекции,
(с) – оптимальная корректирующая функция.
Полученная корректирующая функция имеет вид:
![]() . (8)
. (8)
Существенное отличие аналитического выражения (8) от (6) в том, что ![]() зависит как от текущего состояния системы, так и от величины возмущения
зависит как от текущего состояния системы, так и от величины возмущения ![]() . Оптимальная коррекция приводит к подавлению неустойчивой динамики и переходу в режим модулированных колебаний. Для соотношения частот
. Оптимальная коррекция приводит к подавлению неустойчивой динамики и переходу в режим модулированных колебаний. Для соотношения частот ![]() результаты оказались аналогичными.
результаты оказались аналогичными.
Возможности метода параметрической коррекции были также апробированы на различных системах, способных демонстрировать неустойчивые и хаотические режимы (нелинейные осцилляторы, уравнение Ван дер Поля и его модификации и др.). Коррекции подвергалась динамика как исходных (автономных) систем, так и систем в присутствии периодического внешнего воздействия. При этом рассматривались варианты хаотизации внешним силовым и параметрическим возмущением. Исследованию также подверглись трехмерные системы Лоренца, Ресслера, Чуа и др., которым при соответствующих значениях параметров свойственно наличие хаотического аттрактора.
Несомненным достоинством предложенного метода является возможность аналитически получить оптимальные корректирующие функции и корректировать поведение объекта в случае возникновения неустойчивого или хаотического поведения.
СПИСОК ЛИТЕРАТУРЫ
1. Андриевский Б.Р., Фрадков А.Л. //Автоматика и телемеханика. 2003. №5. С.3-45.
2. Кузнецов А.П., Кузнецов С.П., Рыскин Н.М. Нелинейные колебания. – М.: Изд-во физ.-мат. лит, 2002. 292 с.
3. Лоскутов А.Ю. //Вестник МГУ. 2001. №2. С.3-21.
4. Фрадков А.Л. Кибернетическая физика: Принципы и примеры. – СПб.: Наука, 2003. 208с.
** Работа выполнена при финансовой поддержке Министерства образования и науки РФ.



