Scientific journal

Modern problems of science and education

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Современное образование характеризуется интенсивным использованием информационных технологий, распространением дистанционного обучения, что делает актуальным внедрение как в процесс обучения, так и в процесс самостоятельной работы студентов над учебным материалом автоматизированных обучающих систем. Однако современные автоматизированные обучающиеся системы ориентированы на «усредненного» студента, не учитывают индивидуальных особенностей и начального уровня развития когнитивных способностей, что не позволяет обучающимся в полной мере усвоить предлагаемый учебный материал [5, 6].

Предлагаемая нами методика проектирования этапов образовательного процесса для автоматизированной системы обучения обладает рядом особенностей и преимуществ, поскольку учитывает зону «ближайшего развития» когнитивных способностей обучаемых. Для этого весь учебный материал в рамках конкретной дисциплины дифференцируется не только по разделам, но и по уровням сложности. Переход от раздела к разделу сначала происходит внутри одного уровня [7]. После успешного освоения материала текущего уровня обучаемый переходит на следующий и изучает все разделы дисциплины на нем. Дифференцирование по уровням означает не столько усложнение самих заданий, сколько применение более сложных методов решения, более универсальных способов обработки информации. Кроме того, обучение на текущем уровне одного модуля требует знаний материала другого модуля предыдущего уровня. Таким образом, образовательный процесс развивается по спирали, позволяя последовательно осваивать учебный материал по нарастающим уровня сложности, что позволяет обеспечить динамичность и дифференцированность усвоения учебного материала, при этом использование автоматизированной системы обучения дает возможность индивидуализировать образовательный процесс. Более подробно данный подход изложен в работе [2], а пример организации учебного процесса – в работах [4, 8].

При проектировании образовательного процесса для автоматизированной системы обучения процесс освоения дисциплины предполагал четыре уровня освоения.

Первый уровень освоения дисциплины – начальный, на нем происходит ознакомление с основным содержанием дисциплины, излагаются основные теоретические знания и базовые приемы решения задач. Второй уровень становится доступным только при успешном прохождении первого. Можно сказать, что успешное прохождение второго уровня означает «удовлетворительную» степень освоения учебного материала всего курса. Третий и четвертый уровни означают «хорошую» и «отличную» степени освоения учебного материала. Мы задали четыре уровня сложности для того, чтобы проекция уровня на оценку была проста и понятна. Собственно, количество уровней может быть сколь угодно большим.

Таким образом, содержательная часть автоматизированной системы представляет собой матрицу учебных модулей, номера которых составлены из номера уровня и номера раздела (табл. 1). Здесь количество разделов соответствует количеству разделов учебной дисциплины, для освоения которой проектируется автоматизированная система обучения.

Таблица 1

Структура обучающей системы

Каждый учебный модуль – это комплект дидактических материалов, состоящий из теоретической, практической и тестовой частей. В результате обучения на (i,j)-модуле студент получает оценку Q(i,j). Этот результат может быть интерпретирован как оценка качества освоения учебного материала [1].

Для формирования оценки (i,j)-модуля нам необходимы оценки знаний теоретического и практического материала.

Знание теории мы будем оценивать с помощью тестов. Тестовые вопросы категориально делятся на декларативные и процедурные. Декларативные вопросы оценивают полноту знаний — COM(i,j), процедурные – целостность знаний – INT(i,j). Каждая из этих оценок является метрической, т.е. принадлежит интервалу [0, 1]. Получить такую оценку можно делением количества правильных ответов на количество всех вопросов; если же вопросы неравнозначны, то делением суммы весовых коэффициентов правильных ответов на сумму весовых коэффициентов всех вопросов. Имея оценки полноты и целостности, получим оценку глубины знаний – DEP(i,j) [1]:

Владение практическим материалом будем оценивать с помощью задач. Каждой задаче модуля поставим в соответствие ее сложность – время решения этой задачи экспертом [3]. Обозначим сложность k-й задачи модуля (i,j) через t(i,j,k), а оценку, которую выставит преподаватель за решение этой задачи, – через q(i,j,k) (q(i,j,k)∈[0, 1]). Таким образом, результатом решения k-й задачи (i,j)-модуля будет значение q(i,j,k) * t(i,j,k). Обозначив через R(i,j) оценку качества владения практическим материалом, получим:

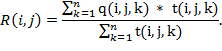
Заметим, что, R(i,j) ∈ [0, 1].

Оценив знание теории и владение практическим материалом, можем получить значение Q(i,j). Оно формируется в соответствии с правилами рейтинговой системы оценивания, принятыми в Казанском национальном исследовательском технологическом университете, где из 100 возможных 60 баллов выделяется для оценивания практической части и 40 – теоретической.

Заметим, что значение Q(i,j) Î [0, 1], и, чем ближе оно к единице, тем более качественно освоен учебный материала (i,j)-модуля.

Теперь мы можем сформировать оценку качества освоения учебного материала i-го уровня – Q(i):

Заметим, что значение Q(1) Î [0, 1], и, чем ближе оно к единице, тем более качественно освоен учебный материал i-го уровня.

Очевидно, что абсолютная единица может быть достигнута в редких случаях. Для «хорошей» степени освоения учебного материала достаточно оценки не ниже 0,75 [2]. Это значение мы будем считать пороговым для прохождения обучаемого на следующий уровень.

Для наглядности все формируемые уровневые оценки приведем в табличном виде (табл. 2).

Таблица 2

Уровневые оценки качества освоения учебного материала

Получив оценки качества освоения учебного материала конкретным лицом, мы можем построить так называемую диаграмму развития обучаемого. На ней наглядно показывается уровень освоения дисциплины этого студента.

Пусть, например, некоторый студент на данный момент времени освоил только 2 уровня с оценками Q(1)=0,8, Q(2)=0,7. Тогда его диаграмма оценки качества освоения учебного материала представлена на рисунке.

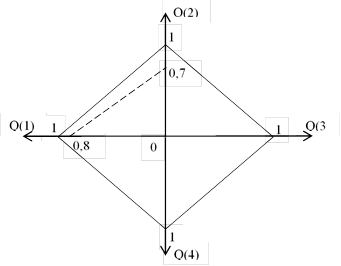
Диаграмма оценки качества освоения учебного материала

Предложенный подход может быть использован и для оценки результатов процесса обучения. Как известно, в соответствии с Положением о балльно-рейтинговой системе оценивания результатов обучения в Казанском национальном исследовательском технологическом университете для получения оценки «отлично» студенту требуется набрать не менее 87 баллов из 100 возможных, оценки «хорошо» — не менее 73 баллов, оценки «удовлетворительно» — не менее 60 баллов.

Как было сказано выше, первый уровень освоения дисциплины в нашей системе считается начальным. Получив на нем оценку Q(1)³0,75, студент допускается на второй уровень, который соответствует «удовлетворительной» степени освоения учебного материала всего курса. Это значит, что студент, получивший оценку Q(2)³0,75, может быть аттестован в рейтинговой системе с оценкой «удовлетворительно». Таким образом, оценке второго уровня нужно сопоставить рейтинговые значения от 60 до 72 баллов. Соотнесем Q(2)=0,75 с 60 баллами, а Q(2)=1 с 72. Получим формулу перехода от оценки автоматизированной системы к рейтингу:

Третий уровень соответствует «хорошей» степени освоения учебного материала всего курса. Это значит, что студент, получивший оценку Q(3)³0,75, может быть аттестован в рейтинговой системе с оценкой «хорошо». Таким образом, оценке третьего уровня нужно сопоставить рейтинговые значения от 73 до 86 баллов. Соотнесем Q(3)=0,75 с 73 баллами, а Q(3)=1 с 85. Получим формулу перехода от оценки автоматизированной системы к рейтингу:

Аналогичным образом для четвертого уровня сопоставим диапазон рейтинговых значений [87, 100] и получим формулу:

Здесь нужно заметить, что высокое пороговое значение перехода, равное 0,75, позволяет при расчете рейтинга последнего пройденного уровня не учитывать оценки уровней предыдущих [7].

Предложенный подход был реализован при проектировании этапов образовательного процесса для автоматизированной системы обучения дисциплине «Методы оптимизации». Дисциплина «Методы оптимизации» содержит следующие разделы:

1. Прямые методы поиска безусловного экстремума.

2. Градиентные методы поиска безусловного экстремума.

3. Задачи линейного программирования.

4. Задачи нелинейного программирования.

Учебный материал каждого раздела был распределен по четырем уровням, образуя тем самым четыре учебных модуля.

Раздел 1.

Модуль (1,1) — Ведение. Основные определения.

Модуль (2,1) — Прямые методы поиска безусловного экстремума функции одной переменной. Методы дихотомии и золотого сечения.

Модуль (3,1) — Прямые методы поиска безусловного экстремума функции одной переменной. Методы Фибоначчи и Пауэлла.

Модуль (4,1) — Метод конфигураций (Хука—Дживса).

Раздел 2.

Модуль (1,2) — Применение производной для нахождения экстремума функции в задачах безусловной оптимизации.

Модуль (2,2) — Градиентные методы для функций многих переменных. Метод покоординатного спуска и метод градиентного спуска с постоянным шагом.

Модуль (3,2) — Градиентные методы для функций многих переменных. Метод наискорейшего градиентного спуска.

Модуль (4,2) — Метод Ньютона.

Раздел 3.

Модуль (1,3) — Основные формы и виды задач линейного программирования. Модели экономических задач. Графический метод решения ЗЛП.

Модуль (2,3) — Двойственная задача линейного программирования. Метод потенциалов решения транспортной задачи.

Модуль (3,3) — Симплекс-метод решения ЗЛП.

Модуль (4,3) — Метод искусственного базиса. Метод Гомори.

Раздел 4.

Модуль (1,4) — Постановка задачи нелинейного программирования. Графический метод решения ЗНП.

Модуль (2,4) — Необходимые и достаточные условия условного экстремума.

Модуль (3,4) — Метод линеаризации Франка—Вулфа.

Модуль (4,4) — Метод штрафных функций.

Такое построение учебного процесса позволяет обеспечить содержательную взаимосвязь как между модулями одного уровня сложности, так и между разноуровневыми модулями одного либо разных разделов.

Реализация данного подхода при проектировании процесса освоения дисциплины «Методы оптимизации» в автоматизированной системе обучения позволяет эффективно обучаться студентам с разным начальным уровнем знаний и когнитивных способностей, последовательно расширяя «зону комфорта», а также оценивать результативность образовательного процесса в динамике, переходя от одного уровня сложности к другому, обеспечивая при этом возможность перехода к традиционной системе оценивания.