Нелокальные краевые задачи для смешанных уравнений составляют широкий класс задач, теория которых интенсивно развивается на протяжении нескольких десятилетий [1-7]. Эти задачи представляют как теоретический интерес, так и обладают прикладной значимостью. Они применяются при моделировании процессов тепло- и массопереноса, описании проблем гидродинамики, решении инженерно-технических задач. В настоящей работе исследована нелокальная краевая задача для смешанного уравнения третьего порядка в характеристической области, которая обобщает результаты работ [8-10] и служит продолжением исследований, начатых в работах [11-13].
1. ПОСТАНОВКА ЗАДАЧИ
Рассматривается уравнение
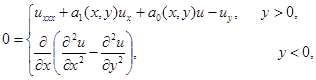 (1)
(1)
в конечной области ![]() , ограниченной отрезками
, ограниченной отрезками ![]() ,
, ![]() и
и ![]() прямых
прямых ![]() и
и ![]() соответственно, а также характеристиками
соответственно, а также характеристиками ![]() и
и ![]() уравнения (1).
уравнения (1).
Пусть ![]() ,
, ![]() ;
; ![]() ,
, ![]() - аффиксы точек пересечений характеристик уравнения (1), выходящих из точки
- аффиксы точек пересечений характеристик уравнения (1), выходящих из точки ![]() с характеристиками
с характеристиками ![]() ,
, ![]() соответственно.
соответственно.
Для уравнения (1) в области ![]() исследована следующая
исследована следующая
Задача 1. Найти функцию ![]() , обладающую свойствами:
, обладающую свойствами:
1. ![]() - регулярное решение уравнения (1) в
- регулярное решение уравнения (1) в ![]() ,
, ![]() ;
;
2. ![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
;
3. ![]() — удовлетворяет граничным условиям:
— удовлетворяет граничным условиям:
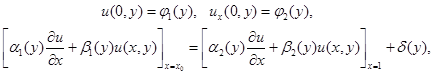 (2)
(2)
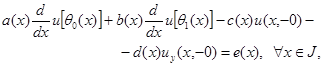 (3)
(3)
![]() (4)
(4)
и условиям сопряжения
![]() (5)
(5)
![]() , (6)
, (6)
где ![]() — внутренняя нормаль. Относительно коэффициентов уравнения (1) и заданных функций здесь и в дальнейшем предполагается, что
— внутренняя нормаль. Относительно коэффициентов уравнения (1) и заданных функций здесь и в дальнейшем предполагается, что
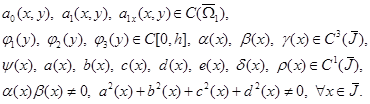
Под регулярным будем понимать решение ![]() уравнения (1), производные которого до порядка, входящего в уравнение, существуют и непрерывны в рассматриваемой области
уравнения (1), производные которого до порядка, входящего в уравнение, существуют и непрерывны в рассматриваемой области ![]() при
при ![]() .
.
Искомую функцию ![]() представим в виде:
представим в виде:
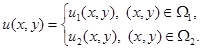
Пусть
![]() (7)
(7)
![]() , (8)
, (8)
тогда условия согласования примут вид
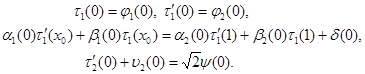
Воспользуемся тем, что любое регулярное решение уравнения (1) при ![]() представимо в виде:
представимо в виде:
![]() ,
,
где ![]() — регулярное решение уравнения
— регулярное решение уравнения
![]() ,
,
а ![]() — дважды непрерывно дифференцируемая функция, которую можно подчинить условию
— дважды непрерывно дифференцируемая функция, которую можно подчинить условию ![]() .
.
Решение уравнения (1) в ![]() представимо в виде [1]:
представимо в виде [1]:
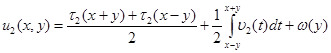 , (9)
, (9)
где 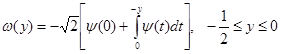 .
.
Подставив (9) в краевое условие (3), получим функциональное соотношение между ![]() и
и ![]() , принесенное из гиперболической части
, принесенное из гиперболической части ![]() на линию
на линию ![]() в виде:
в виде:
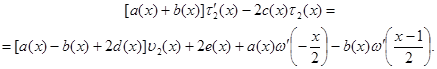 (10)
(10)
Переходя к пределу в уравнении (1) при ![]() , получим соотношение между
, получим соотношение между ![]() и
и ![]() :
:
![]() . (11)
. (11)
На основании (7), (8) условия склеивания (5), (6) примут вид:
![]() , (12)
, (12)
![]() . (13)
. (13)
Пусть ![]() , тогда (10) представимо в виде:
, тогда (10) представимо в виде:
![]() , (14)
, (14)
где ![]() ,
, ![]() ,
,
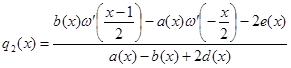 .
.
Из (12), (13) и (14) найдем ![]() :
:
![]() , (15)
, (15)
где ![]() ,
, ![]() ,
,
![]() .
.
Подставляя ![]() из (15) в (11) и учитывая граничные условия (2), приходим к задаче для определения
из (15) в (11) и учитывая граничные условия (2), приходим к задаче для определения ![]() :
:
![]() , (16)
, (16)
![]() (17)
(17)
где ![]() ,
, ![]() .
.
2. ЕДИНСТВЕННОСТЬ РЕШЕНИЯ ЗАДАЧИ 1
Пусть ![]()
![]()
![]()
![]() .
.
Теорема. Если выполняются условия:
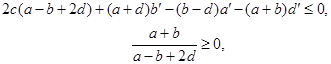 (18)
(18)
![]() , (19)
, (19)
тогда ![]() .
.
Доказательство. Рассмотрим интеграл
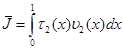 .
.
С учетом (14) получим:
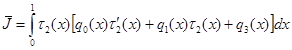 .
.
После несложных преобразований этот интеграл можно переписать в виде:
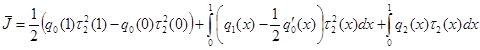 . (20)
. (20)
Из условий (18) заключаем, что
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Таким образом
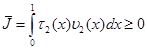 . (*)
. (*)
С другой стороны, из условий склеивания на основании (11) имеем:
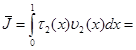
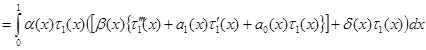 .
.
После преобразований, получим:
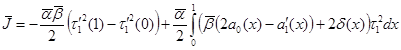 . (21)
. (21)
Из условия (19), заключаем, что
![]() ,
,
и, следовательно,
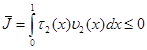 . (**)
. (**)
Сравнивая (*) и (**), заключаем, что ![]() . Тогда
. Тогда
![]() .
.
По схеме, предложенной в работе [2], доказывается, что ![]() в области
в области ![]() .
.
3. СУЩЕСТВОВАНИЕ РЕШЕНИЯ ЗАДАЧИ 1
Интегрируем (16) три раза от 0 до ![]() , получим:
, получим:
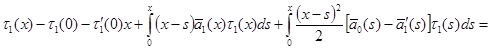
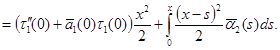
Откуда 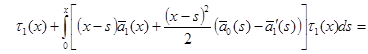
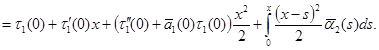
Обозначая 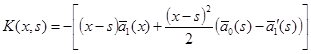 ,
,
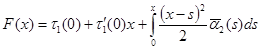 ,
, ![]() ,
,
перепишем последнее выражение в виде:
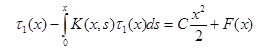 . (22)
. (22)
Если обозначить через
![]() ,
,
будем иметь:
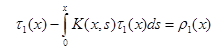 . (22’)
. (22’)
Обращая (22’) через резольвенту ![]() ядра
ядра ![]() , получим:
, получим:
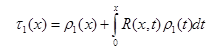 , (23)
, (23)
или 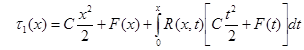 .
.
Откуда 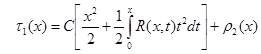 ,
,
где 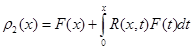 .
.
Продифференцировав (23), получим:
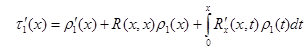
или 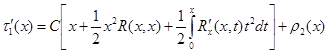 ,
,
где 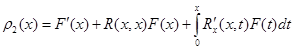 .
.
Для определения ![]() воспользуемся третьим условием (17). Будем иметь:
воспользуемся третьим условием (17). Будем иметь:
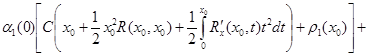
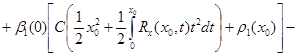
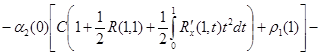
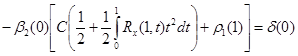 .
.
Если обозначить через
![]() ,
,
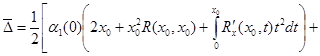
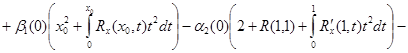
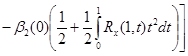 ,
,
то при условии, что ![]() , найдем
, найдем ![]() :
:
![]()
и, следовательно, для определения неизвестного ![]() будем иметь следующую формулу:
будем иметь следующую формулу:
![]() .
.
После определения функций ![]() из формул (15), (12), (13) решение задачи 1 в области
из формул (15), (12), (13) решение задачи 1 в области ![]() находится по формуле (9), а в области
находится по формуле (9), а в области ![]() приходим к следующей задаче: (1), (2),
приходим к следующей задаче: (1), (2), ![]() , существование решения которой доказывается с помощью преобразований Лапласа.
, существование решения которой доказывается с помощью преобразований Лапласа.
Рецензенты:
Шхануков-Лафишев М. Х., д.ф.-м.н., профессор, ФГБУН «Институт информатики и проблем регионального управления Кабардино-Балкарского научного центра РАН», г. Нальчик;
Журтов А.Х., д.ф.-м.н., профессор кафедры ГиВА Кабардино-Балкарского государственного университета, г. Нальчик.



