Целью настоящей работы является анализ областей применимости математических моделей взаимосвязанных организационно-технологическихпроцессов. Применяемый подход основан на использовании теории нечетких множеств и отношений [11], что отличает его от стохастических подходов, используемых в [7,8], и дает новые возможности для выбора моделей изучаемых процессов.
Математическое моделирование взаимосвязанных организационно-технологических процессов
Будем предполагать (в соответствии с [4,5]), что исследуемые взаимосвязанные процессы Z1(t),Z2(t), …, ZK(t), рассматриваемые во временном интервале tнач£t£tкон, допускают аддитивное математическое описание
Z1(t)= f11(t,Z1(t-1))+ f 12(t,Z2(t-1))+…+ f 1K(t,ZK(t-1)
Z2(t)= f21(t,Z1(t-1))+f 22(t,Z2(t-1))+…+ f 2K(t,ZK(t-1)
…
ZK(t)=fK1(t,Z1(t-1))+fK2(t,Z2(t-1))+…+ fKK(t,ZK(t-1))
где
диагональные слагаемые отражают «эффект памяти» (зависимость значений текущих
параметров процесса от предыдущих значений), а остальные слагаемые отражают
взаимные влияния процессов. При решении некоторых задач связями между
отдельными процессами можно пренебречь, что дает возможность использования
упрощенных соотношений, не включающих соответствующие слагаемые. Таким образом,
каждой матрице связности вершин (aij) i,j=1,2,…,
K, построенной для графа взаимосвязей
между процессами, может быть поставлена в соответствие некотораяупрощенная
модель. При этом матрица, состоящая из единиц aij=1 (i,j=1,2,…, K), соответствует полно
связной модели, а единичная матрицаaij=1 при i=j , aij=0 при i¹j (i,j=1,2,…, K) – модели, не
учитывающей связей между процессами. В общем случае упрощенная модель может
быть представлена бинарной квадратной матрицей, что удобно при описании всего
конечного множествавозможных моделейвзаимосвязанных процессовMATMOD, мощность которого (при большом
числе рассматриваемых процессов) может быть достаточно велика: |MATMOD |=![]() .
.
Использование упрощенных моделей взаимосвязанных процессов позволяет сократить затраты на выполнение вычислительных экспериментов, что делает актуальной проблему описания и синтеза (выбора из заданного множества) моделей для решения заданного круга задач.
Нечеткие отношения и операции над математическими моделями
Рассмотрим конечную совокупность задач предметной области, для решения которых могут быть использованы рассматриваемые модели:Tasks = {Task1, Task2,…, Taskn,…, TaskN}. В рамках конкретной предметной области множество Tasks соответствует понятию универсума задач.
Обозначим TaskMatMod – множество задач, которые могут быть решены с использованием конкретной модели MatMod, которое назовем множеством (областью) применимости модели MatMod. Тогда TaskMatModÍTasks, т.е. множество применимости конкретной модели является подмножеством всей совокупности задач предметной области.
Наряду с задачами, безусловно решаемыми
с использованием модели MatMod,
целесообразно рассмотреть задачи, которые до некоторой степени могут быть
решены с использованием MatMod.Обозначим![]() askMatMod– нечеткое множество применимости:
askMatMod– нечеткое множество применимости:
![]() askMatMod= {( Taski,μi)| i=1,2,…,N}, где функция принадлежности μi =μ(Taski) принимает значения на отрезке [0, 1] и
отражает определяемую экспертами степень соответствия модели MatModзадачам Task1,Task2,…,TaskN.Носителем нечеткого множества
askMatMod= {( Taski,μi)| i=1,2,…,N}, где функция принадлежности μi =μ(Taski) принимает значения на отрезке [0, 1] и
отражает определяемую экспертами степень соответствия модели MatModзадачам Task1,Task2,…,TaskN.Носителем нечеткого множества ![]() askMatModявляется совокупность задач, хоть в
какой-то степени решаемых моделью MatMod :
askMatModявляется совокупность задач, хоть в
какой-то степени решаемых моделью MatMod :
Supp(![]() askMatMod ) = {Taski| μ(Taski)>0,
i=1,2,…,N}
askMatMod ) = {Taski| μ(Taski)>0,
i=1,2,…,N}
Ядро нечеткого множества![]() askMatMod представляет собой совокупность задач,
в полной мере решаемых модельюMatMod :
askMatMod представляет собой совокупность задач,
в полной мере решаемых модельюMatMod :
Kern(![]() askMatMod ) = {Taski| μ(Taski)=1,
i=1,2,…,N}.
askMatMod ) = {Taski| μ(Taski)=1,
i=1,2,…,N}.
Важными частными случаями являются:
- универсальная модельMatModU, позволяющая в полной мере решить весь
рассматриваемый круг задач предметной области:Kern(![]() askMatModU) =Tasks;
askMatModU) =Tasks;
- пустая модельMatMod0, не позволяющая ни в какой степени
решить ни одну задачу из рассматриваемого круга задач предметной области:Supp(![]() askMatMod0) =Æ.
askMatMod0) =Æ.
Будем полагать, что универсальная модельMatModU соответствует полно связной модели (aij=1; i,j=1,2,…, K), пустая модельMatMod0 соответствует несвязной модели без памяти (aij=0; i,j=1,2,…, K), и чторазличным моделям соответствуют несовпадающие множества применимости, т.е.:
MatMod1
≠
MatMod2 Þ ![]() askMatMod1
≠
askMatMod1
≠
![]() askMatMod2.
askMatMod2.
Введем отношение применимости на множестве математических моделей, полагая модель MatMod1не более применимой, чем модель MatMod2, если нечеткое множество применимости модели MatMod1включено в нечеткое множество применимости модели MatMod1,т.е:
MatMod1
ÐMatMod2 ,если![]() askMatMod1Í
askMatMod1Í![]() askMatMod2
askMatMod2
Здесь в соответствии с определением
включения нечетких множеств [10], ![]() askMatMod1Í
askMatMod1Í![]() askMatMod2 означает, что
askMatMod2 означает, что
μ1(Taski) £μ2(Taski)(i=1,2,…,N)
Нетрудно видеть, что так введенное отношение применимости будет отношением частичного порядкана множестве моделейMATMOD, т.к. для него выполняются:
-рефлексивность:MatMod1 ÐMatMod1;
-антисимметричность:
MatMod1ÐMatMod2, MatMod2 ÐMatMod1 Þ MatMod1 =MatMod2;
-транзитивность:
MatMod1ÐMatMod2, MatMod2 ÐMatMod3 Þ MatMod1 ÐMatMod3.
При решении практических задач моделирования зачастую используют несколько моделей. Рассмотрим подмножество MATMOD* множества моделей MATMOD
MATMOD*Í MATMOD
Точной нижней гранью (infimum) множества MATMOD* будет модель MatMod*ÎMATMOD, не превосходящая по применимости все модели этого множества, т.е.
infMATMOD*= MatMod* :MatMod*ÐMatMod, "MatModÎMATMOD*.
В случае, когда модельMatMod*, представляющая собой точную нижнюю грань множества MATMOD*, является элементом этого множества, она является также минимальным элементом этого множества, т.е.
minMATMOD*=infMATMOD* приinfMATMOD*ÎMATMOD*.
Понятия точной верхней грани (sup) и максимума (max) применительно к множеству моделей взаимосвязанных процессов (с учетом введенного отношения частичного порядкаÐ) определяются аналогичным образом.Нетрудно видеть, что точные грани существуют для любого множества моделей MATMOD*, поскольку для любой математической модели MatMod выполняются отношения: MatMod0 ÐMatModÐMatModU. Максимальные и минимальные элементы для некоторых множеств могут не существовать.
Основываясь на введенных понятиях точных граней, естественно ввести операции над моделями взаимосвязанных процессов.
Объединением моделейMatMod1 и MatMod2назовем точную верхнюю грань множества, состоящего из этих моделей:
MatMod1 ÈMatMod2 =sup{ MatMod1, MatMod2 }.
Пересечение моделей MatMod1 и MatMod2 назовем точную нижнюю грань множества, состоящего из этих моделей:
MatMod1 ÇMatMod2 =inf{ MatMod1, MatMod2 }.
Упорядочение моделей в соответствии с областями их применимости и введение операций над моделями позволяют формулировать и решать задачи выбора моделей взаимосвязанных процессов.
Использование нечеткогоанализаобластей применимости при выборе моделей
Сформулируем постановку задачиформирования множества моделей для решения заданного круга задач:
Имеется конечное множество моделей M={MatMod1,MatMod2, ….,MatModm}. Задано условие в виде нечеткого
множествазадач,подлежащих решению ![]() ask= {( Taski, μi)| i=1,2,…,N}. Требуется найти минимальное по
мощности множество моделей minMATMOD*ÍM, удовлетворяющее этому условию.
ask= {( Taski, μi)| i=1,2,…,N}. Требуется найти минимальное по
мощности множество моделей minMATMOD*ÍM, удовлетворяющее этому условию.
Математическая постановка задачи имеет вид:
minMATMOD*=argmin(|MATMOD*|),
MATMOD*={MatMod :![]() askÍ
È
askÍ
È![]() askMatMod}
askMatMod}
Для исследования поставленной задачи рассмотрим ориентированный граф упорядочения моделей,где вершины графа – элементы множества М, а дуги – отношения частичного порядка (рис.1). Нетрудно видеть, что искомое множество может быть сформировано из корневых вершин графа, не имеющих входных дуг (полустепень исхода Р- = 0). Однако некоторые корневые вершины графа не обязательно должны входить в искомое множество.
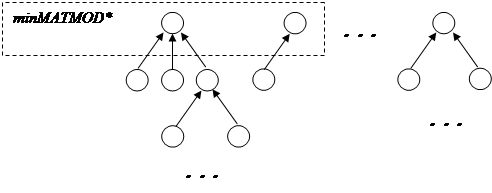
Рис. Граф упорядочения моделей взаимосвязанных процессов с выделенным
подмножеством корневых вершин minMATMOD*
Эвристическая итерационная процедура нахождения решения сформулированной задачи состоит в последовательном уменьшении исходного множества моделей Мдо тех пор, пока выполняется условие и включает в себя следующие этапы:
- Формирование объединения множеств применимости моделей M и проверка условия:
![]() askÍ
askÍ
![]() askM, где
askM, где ![]() askM = È
askM = È![]() askMatMod,MatModÎM.
askMatMod,MatModÎM.
Если условие не выполняется, то конец работы процедуры с сообщением о неразрешимости задачи.
- Последовательное исключение корневых вершин графа и проверка выполнения условия. На последней итерации(пока еще выполняется условие) получается решение, которое является оптимальным (при полном переборе возможных исключений корневых вершин) или рациональным (при случайном выборе корневых вершин, подлежащих исключению и заданном числе итераций).
Выводы
Предложенный подход к проблеме выбора (синтеза) моделей взаимосвязанных организационно-технологических процессов, основанный на применении нечеткого теоретико-множественного аппарата, позволил структурировать совокупность моделей и сформулировать математическую постановку задачи формирования минимального по мощности множества моделей для решения заданного круга задач предметной области. Предложенная эвристическая процедура позволяет найти оптимальное или рациональное (в зависимости от используемого варианта) решение. Подсистема синтеза моделей, основанная на применении предложенного подхода, включена в состав исследовательского прототипа информационно-аналитической системы моделирования организационно-технологических процессов [9]. Предварительные результаты применения разработанной процедуры показали ее эффективность. Дальнейшее развитие предложенного подхода может быть связано выбором модели не только исходя из ее применимости, но и с учетом предполагаемых затрат, связанных с ее применением.
Работа выполнена при финансовой поддержке РФФИ в рамках научных проектов№ 14-07-00246 и № 15-07-05715.
Рецензенты:Дюкарев Ю. М., д.ф.-м.н., доцент, профессор кафедры математики и физики, ФГБОУ ВО «Белгородский государственный аграрный университет им. В.Я. Горина», г. Белгород.
Маторин С. И., д.т.н., профессор,профессор кафедрыприкладной математики и информатики, ФГАОУВПО «Белгородский государственный национальный исследовательский университет», г. Белгород.



