Постановка вопроса. Традиционно анализ устойчивости по Ляпунову (ниже устойчивости) строится на основе качественной теории обыкновенных дифференциальных уравнений (ОДУ). В [3–5] показана возможность численного моделирования устойчивости на основе рекуррентных преобразований разностных решений ОДУ. Такая возможность обусловлена тем, что при условии устойчивости разностные методы накапливают погрешность не более чем линейно по длине промежутка решения [2–4] (доказательства содержатся в [2] и [6, 7]). В статье представлены критерии устойчивости, основанные на рассматриваемых преобразованиях, и результаты численного моделирования. Основная задача излагаемого сообщения заключается в анализе достоверности предложенных критериев устойчивости линейных систем в зависимости от шага разностного метода.

Исходные предположения. Рассматривается задача Коши для системы

(1)

где , , . Предполагается, что существует , при котором все условия существования и единственности выполнены для невозмущенного решения на полупрямой и для каждого его возмущения , , с начальным вектором из окрестности . Здесь и ниже рассматриваются канонические согласованные нормы матрицы и вектора. Предполагается, что в области функция всюду определена, непрерывна и непрерывно дифференцируема по независимой переменной (в точке – справа), компоненты этой функции удовлетворяют неравенству:

. (2)

Определение устойчивости [9] упрощено в принятых ограничениях: решение устойчиво, если найдется , такое, что влечет . Решение асимптотически устойчиво, если оно устойчиво и найдется , такое, что влечет при .

Метод Эйлера решения задачи (1)

(3)

всюду ниже рассматривается в следующем предположении: значение произвольно выбранной независимой переменной остается для (3) фиксированным, при этом индекс неограниченно возрастает с убывающим на равномерным шагом –

. (4)

Изменение независимой переменной понимается как изменение правой границы .

Условия устойчивости в мультипликативной форме. Метод Эйлера рассматривается в виде

, , (5)

где , из (4), – остаточный член формулы Тейлора для -й компоненты приближения: . Для возмущенного решения: , , . Предполагается, если не оговорено иное, что

. (6)

Рассматриваются следующие преобразования возмущения:

,

или

, , (7)

где

. (8)

С учетом (2) при ограничении (6).

Из (7), (8) следует:

, (9)

где , из (4), из (7), . Имеет место

Лемма 1 [3, 4]. В рассматриваемых предположениях для всех решений и их возмущений из выполнено равенство .

Следствие 1. В тех же условиях на основании (9) верно равенство:

. (10)

Теорема 1. В условиях леммы для устойчивости решения задачи (1) необходимо и достаточно существование , такого, что для всех решений , при ограничении выполняется неравенство:

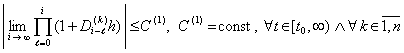. (11)

Для асимптотической устойчивости необходимо и достаточно, чтобы выполнялось предыдущее утверждение и существовало , такое, что влечет:

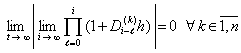. (12)

Можно показать, что выполнение условий леммы 1 обеспечивает равномерную сходимость метода Эйлера на произвольном отрезке полуоси [7].

Разностная форма условий устойчивости. Из (10) следует:

. (13)

Из (13) и теоремы 1 вытекает

Следствие 2 [3]. При формулировка и утверждение теоремы 1 дословно сохраняются при замене соотношения (11) на соотношение вида

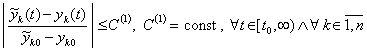, (14)

и (12) – на соотношение

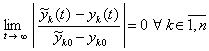. (15)

Следствие 3. Если система (1) имеет точку покоя, то в рассматриваемых условиях для ее устойчивости необходимо и достаточно существование , такого, чтобы для всех решений , при ограничении и выполнялось

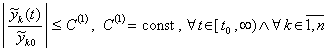, (16)

точка покоя асимптотически устойчива, если выполнено предыдущее утверждение и кроме того существует , такое, что неравенство влечет

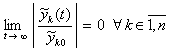. (17)

Компьютерная проверка (14) – (17) совмещается с приближенным решением.

Условия устойчивости систем линейных ОДУ. Можно ограничиться случаем

, (18)

где матрица состоит из функций , которые определены, непрерывны и непрерывно дифференцируемы (в точке – справа) на полуоси .

Следствие 4. Следствие 3 дает необходимые и достаточные условия устойчивости и асимптотической устойчивости всей системы (18) [8].

Следствие 5. Для устойчивости системы (18) необходимо и достаточно выполнение (16) для какого-либо одного решения инвариантного относительно выбора начального вектора , [8].

В дальнейшем используется независимый от начального вектора способ [3, 4], приводимый ниже. Метод Эйлера для задачи (18) представляется в виде

, (19)

где , при каждом и каждом элемент является остаточным членом формулы Тейлора. Аналог (19) для возмущения обозначается . Рекуррентное преобразование влечет [4]:

,

, , – единичная матрица.

Лемма 2. В рассматриваемых условиях .

Следствие 6. В тех же условиях,

.

Теорема 2. Система (18) устойчива тогда и только тогда, когда

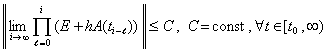. (20)

Для асимптотической устойчивости необходимо и достаточно, чтобы выполнялось (20) и соотношение

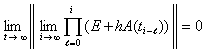. (21)

Эквивалентная запись соотношений (20), (21):

, .

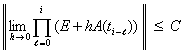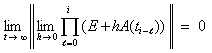Следствие 7. Теорема 2 сохраняется, если матрица постоянна, условия (20), (21) соответственно примут вид: ; .

Степень матрицы можно заменить на [5]:

; . (22)

Следствие 7 не включает ограничений на вид матрицы.

Эксперимент по оценке достоверности критериев устойчивости линейных систем в зависимости от шага разностного метода. При рассмотрении однородных линейных систем вида

, (23)

с целью эксперимента рассматривалась матрица:

.

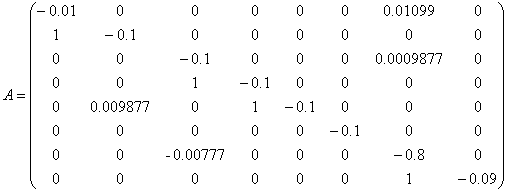Реализация критериев (22) для оценки устойчивости системы (23) в случае данной матрицы показывает асимптотическую устойчивость (что соответствует диагональному преобладанию) при изменении шага в диапазоне . В частности, при получаются следующие значения нормы из (22) (нижняя строка таблицы, в верхней – номер итерации из (22)):

При для той же задачи получаются следующие значения:

В случае матрицы реализация (22) для системы (23) показывает неасимптотическую устойчивость, поскольку сохраняется ограниченность нормы величиной 1.4142 на большом интервале изменения при изменении в диапазоне . При получаются следующие значения нормы из (22):

При получаются значения:

При получится:

Величина интервала, на котором сохраняется верная оценка, а также число возведений в степень сокращаются с ростом шага вследствие накопления погрешности.

Для матрицы 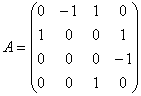реализация (22) показывает неустойчивость на основании быстрого роста нормы, приводящего к переполнению в диапазоне . Переполнение возникает быстрее при более грубом шаге. При для рассматриваемой матрицы получаются следующие значения нормы из (22):

При получится:

Собственные числа матрицы имеют нулевую вещественную часть, кратность элементарного делителя влечет неустойчивость, что подтверждает данный эксперимент.

Заключение. Изложены компьютерные методы анализа устойчивости на основе рекуррентных преобразований разностных решений систем ОДУ. Для линейной системы условия устойчивости инвариантны относительно начального вектора или от него не зависят. Для нелинейной системы необходимым и достаточным условием устойчивости является равномерная ограниченность на полуоси отношения возмущения к вызвавшему его возмущению начальных значений в варьируемой окрестности. Асимптотическая устойчивость имеет место при стремлении этого отношения к нулю с ростом независимой переменной. На этой основе реализуется численное моделирование устойчивости, которое выполняется по ходу разностного решения системы.

Рецензенты:

Боженюк А.В., д.т.н., профессор кафедры информационно аналитических систем безопасности, Инженерно-технологическая академия Южного федерального университета, г. Таганрог;

Карелин В.П., д.т.н., профессор, заведующий кафедрой прикладной математики и информационных технологий Таганрогского института управления и экономики, г. Таганрог.