Scientific journal

Modern problems of science and education

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

В последнее время широкое распространения получила парадигма так называемого глубокого обучения. По существу, она представляет собой развитие классической идеи персептрона [6]. Известно, что сети прямого распространения позволяют решать широкий круг задач классификации, управления, аппроксимации [1]. Основное отличие современного подхода заключается в использовании не одно- или двухслойных сетей, а создание сетей с большим количеством слоёв. Этим объясняется использование приставки «глубокое» в термине deeplearning. Применение множества слоёв позволяет решать более сложные задачи. Например, такие, в которых предъявляются особенно жёсткие требования к инвариантности реакций сети при преобразованиях масштабирования и поворота входных образов.

При решении задачи разработки искусственной нейронной сети приходится сталкиваться с различными сложностями. Одна из главных проблем связана с тем, что увеличение количества слоёв (глубины) сети, с одной стороны, увеличивает обобщающий потенциал, а с другой, приводит к экспоненциальному росту количества синапсов, т.е. свободных параметров модели. Это в свою очередь существенно замедляет процесс обучения и приводит к проблеме переобучения. А это в свою очередь ведёт к экспоненциальному увеличению вычислительной сложности модели.

Решением является отказ от полносвязности слоёв. В классической схеме персептрона каждый нейрон связывался с каждым нейроном из предыдущего слоя, следовательно, количество синапсов было пропорционально количеству нейронов. Для решения этой проблемы была разработана концепция сверточных нейронных сетей [3].

При помощи сверточных нейронных сетей наиболее эффективно решаются задачи распознавания образов. По этой причине многие крупные компании уже представили свои программные библиотеки для решения задач глубокого обучения свёрточных нейронных сетей [4,5]. При этом основной упор делается на реализации использующих технологию вычислений общего назначения на графических ускорителях (GPGPU). Структура этих ускорителей превосходно подходит для решения задач deeplearning [4].

Применение сверточных слоёв позволяет решить вопросы, связанные с управлением вычислительной сложностью модели. Однако она не решает множества сопутствующих вопросов. Выбор количества нейронов, выбор параметров активационной функции, выбор параметров обучения. Для этих целей используются так называемые конструктивные алгоритмы. Эти алгоритмы позволяют автоматизировать процесс выбора архитектуры сети. Это приводит к неоправданному росту размерности модели, и, как следствие, снижает её эффективность. В статье представлен метод, позволяющий повысить эффективность конструктивных алгоритмов. Благодаря предлагаемому методу нейрон может адаптировать параметры активационной функции к размерности входных воздействий таким образом, чтобы его выходное значение всегда оставалось вне зоны насыщения. Таким образом, независимо от того, как конструктивный алгоритм изменит топологию сети, все нейроны гарантированно будут принимать участие в работе сети.

Алгоритм адаптации параметров активационной функции

При разработке структуры сети приходится сталкиваться с проблемой выбора параметров активационной функции. Для сигмоидальной функции нужно указать два параметра: смещение и угол наклона. Если параметры будут заданы неверно, то превышение входными значениями определённого порога приведёт к тому, что выходное значение нейрона будет равным максимально возможному выходу, следовательно, нейрон становится нечувствительным к любым изменениям входа за пределами этого порога. Это особенно актуально при использовании конструктивных алгоритмов, в которых конфигурация сети постоянно изменяется, и, следовательно, невозможно заранее определить параметры активационной функции.

Для решения проблемы предлагается встроить в нейроны адаптационный алгоритм выбора параметров активационной функции, который бы предотвращал проблему переполнения нейрона, автоматически определяя корректные параметры. Для этого параметры активационной функции сами определяются как функции от параметра. В данной работе рассматривается работа с сигмоидальной функцией, но аналогичные рассуждения могут быть проведены для других видов активационных функций.

(1)

В работе [2] даются общие рекомендации по настройке параметров сигмоидальной функции

, (2)

где a – определяет угол наклона сигмоиды, а b – определяет смещение сигмоиды относительно начала координат, s – суммарный вход нейрона (индуцированное локальное поле). В работе [2] указывается, что значения параметров получаются экспертным путём. Коэффициент наклона можно вычислить на основе оценки значения выхода в точке, соответствующей максимальному выходному значению сигнала. Например, 0.99. Аналогично смещение получается из значения входа при выходном сигнале равном 0.5.

Таким образом, вид активационной функции зависит от максимально возможного индуцированного локального поля. От его значения зависит как коэффициент наклона, так и смещение сигмоиды. Поскольку

,

где – i-й вход нейрона, – вес i-го входа. И учитывая, что

не сложно видеть, что максимальный вход определяется формулой

,

где max – максимально возможное значение индуцированного локального поля нейрона.

Исходя из вышеизложенного, формулы для расчёта параметров активационной функции имеют вид: угол наклона

,

смещение

.

Таким образом, алгоритм работы нейрона принимает вид:

1. Рассчитать максимальный вход max.

2. Рассчитать индуцированное локальное поле s.

3. Определить параметры активационной функции a и b.

4. Вычислить выходное значение нейрона y.

Теперь при определении структуры сети инженер может не беспокоиться о выборе параметров активационной функции. Как бы не изменялась размерность входного вектора, нейрон автоматически подстроится к новой размерности, и выход нейрона всегда будет оставаться корректным. Это особенно удобно при использовании парадигмы растущих сетей, поскольку заранее оценить максимальную размерность входного вектора каждого нейрона невозможно. При этом выход нейрона не только будет оставаться корректным, но также будет поддерживаться достаточно высокое его значение. Таким образом, сеть одновременно предохраняется как от перенасыщения, так и от вырождения.

Модификация алгоритма обучения

Основным методом обучения сетей прямого распространения является метод обратного распространения ошибки. Он в свою очередь основывается на стохастическом градиентном спуске. Если обозначить обновление параметра x в момент времени t как формула обновления параметра будет иметь вид:

Алгоритм градиентного спуска пошагово оптимизирует параметры модели, используя формулу

(3)

где,n – параметр скорости обучения. От этого параметра зависит размер шага модификации параметров. Если шаг будет малым, процесс обучения будет происходить медленно, если шаг будет слишком большим, обучение не сможет обнаруживать локальные минимумы.

Существует ряд модификаций классического алгоритма градиентного спуска. Они основываются на методе Ньютона

, (4)

где –матрица обратная матрице Гессе вторых производных, вычисленных для итерации t. В чистом виде на практике данный метод не применим из-за высокой вычислительной стоимости.

Поскольку для управления обучением невозможно использовать точные методы, выбор квазиоптимального параметра обучения является частью инженерной сложности в задаче обучения нейронной сети.

Существуют различные алгоритмы аппроксимирующие формулу (4). В работе [7] рассматривается один из таких алгоритмов, под названием Adadelta. Он позволяет:

- отказаться от ручного выбора параметра обучения;

- обеспечить нечувствительность к значениям параметров обучения;

- производить обучение с различной скоростью по каждому из параметров;

- уменьшить количество итераций при градиентном спуске;

- снизить зависимость обучения от начальных условий;

- возможность использовать один алгоритм для глобального и локального поиска.

Алгоритм имеет следующий вид. Сначала рассчитывается экспоненциальное среднее градиента:

,

где – коэффициент затухания во времени, – параметр для улучшения свойств знаменателя [8]. В [7] указывается, что работа алгоритма не зависит существенным образом от выбора этих параметров.

После чего рассчитывается текущее приращение

И затем рассчитывается экспоненциальное среднее приращений

Более подробно алгоритм рассмотрен в работе [7]. Выбор параметра n происходит в автоматическом режиме в зависимости от хода процесса обучения, и при решении задачи многомерной оптимизации процесс обучения управляется по всем размерностям в отдельности.

Введение адаптационных поправок в алгоритм работы нейрона приводит к необходимости изменения стандартного алгоритма обратного распространения ошибки. Модификация весовых коэффициентов нейронов производится по формуле (3). В качестве f(x) выступает функция ошибки E(w), где w это значение весов синапсов. По правилу дифференцирования сложной функции

Таким образом, при использовании классической сигмоидальной функции

где q – номер слоя, а определяется в зависимости от номера слоя.

,

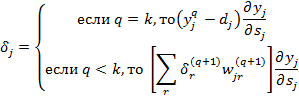
где k –количество слоёв нейронов, q – номер слоя.

Однако адаптивная сигмоида (2) имеет более сложную формулу по сравнению с исходной (1). Её значение зависит в частности от значения весов нейрона. Поэтому требуется внести изменения в расчеты сложной производной от функции ошибки.

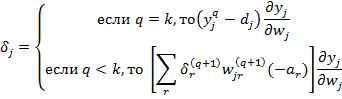
Приведённые формулы включают изменения, вносимые адаптационным алгоритмом в процесс прямого распространения сигнала по сети, и учитывают их в реализации алгоритма градиентного спуска.

Тестирование рассмотренных алгоритмов

Описанные алгоритмы требуют большего объема памяти по сравнения с традиционными, поскольку вынуждены сохранять дополнительные данные между разными этапами передачи сигнала и обучения. Кроме того, они имеют большую вычислительную сложность, поскольку вводят дополнительные параметры, часть из которых рассчитывается динамически. Для оценки реального изменения сложности был проведён ряд экспериментов. При тестировании использовались данные из [10]. Данные представляют собой изображения цифр 28x28 пикселов. Во время теста использовалась сеть прямого распространения, архитектурно аналогичная сети из [9]. Средние значения, полученные в результате тестовых запусков, сведены в таблицу 1.

Таблица 1

Результаты тестирования

Для оценки работы рассмотренных алгоритмов использовались 4 реализации:

А1 – без применения рассмотренных методов. Параметры нейронов и обучения выбирались вручную. В таблице 1 приводятся лучшие результаты.

А2 – без адаптации нейронов, но с алгоритмом Adadelta.

А3 – с алгоритмом адаптации нейронов, но без Adadelta

А4 – с алгоритмом адаптации нейронов и с алгоритмом Adadelta.

Как видно, скорость сходимости в эпохах у А4 значительно превосходит результаты других алгоритмов. Поскольку условия тестирования всех алгоритмов были идентичными и результаты, занесённые в таблицу, являются статистическими, можно предположить, что это связано с синергетическим эффектом, который возникает при взаимодействии алгоритма Adadelta с адаптационным алгоритмом. В то же время скорость сходимости по времени всего на 15 % меньше, чем у A3. Это связано с большей вычислительной сложностью алгоритма А4 по сравнению с остальными. Расход памяти при применении адаптационного алгоритма заметно больше, однако в условиях быстрого роста объёмов памяти современных ЭВМ этот параметр нельзя назвать существенным. Средняя ошибка А4 лишь незначительно хуже, чем у алгоритма А3. Это означает, что адаптационный алгоритм снижает качество локального поиска, однако, учитывая малость абсолютного значения ошибки, данный недостаток не представляется существенным.

Заключение

Предложенный алгоритм адаптации параметров сигмоидальной функции, а также алгоритм Adadelta, уменьшают сложность задачи проектирования и реализации нейросетевых моделей. Это позволяет в частности снизить требование к инженерной квалификации специалиста, разрабатывающего нейросетевое решение, а, следовательно, позволяет расширить сферу применения нейросетевых алгоритмов, включив в неё специалистов из смежных отраслей знаний.

Синергетический эффект, возникающий при совместном применении двух алгоритмов, позволяет существенно повысить технические характеристики получаемых нейросетевых решений. Это стимулирует к поиску других алгоритмов, которые также позволят повысить эффективность сетей прямого распространения. В частности, открытым остаётся вопрос о выборе оптимального количества нейронов для решения конкретной задачи. Применение конструктивных алгоритмов требует значительных вычислительных ресурсов. Однако предложенный адаптационный алгоритм повышает степень автоматизации процесса синтеза структуры сети, предлагая механизм автоматического учета новых синаптических связей, без ограничения их количества на нейрон. При этом каждый нейрон сети избегает и вырождения, и перенасыщения. Таким образом, предложенный алгоритм является органической частью более широкой концепции, решающей не только технические, но инженерные вопросы проектирования нейронных сетей.

Рецензенты:

Галушкин Д.Н., д.т.н., доцент, профессор кафедры «Информатика», институт сферы обслуживания и предпринимательства (филиал) ДГТУ, г. Шахты.

Лебедев Б.К., д.т.н., профессор, профессор кафедры «Системы автоматизации проектирования», ФГОУ ВПО «Южный федеральный университет», г. Таганрог.