Одним из главных этапов разработки эффективной системы управления организации является формирование структуры на основе анализа и синтеза систем.
Данный анализ и синтез рассматриваемых систем предполагает приведение в соответствие структуры организации ее целям, задачам и требованиям.
Анализ и синтез структур ОС производится по следующим этапам для определения:
- структур ОС;
- в формализованном виде описание функционирования элементов структуры ОС;
- целей каждого из элементов структуры ОС;
- корректирующих изменений в структуре ОС.
Конкретный вид структуры ОС должен соответствовать нормативным документам, определяющим необходимость достижения главной цели этой организации. Но в связи с тем, что в наше время динамически изменяются требования к ОС в соответствии с нормативными документами, принимаемыми государственными структурами, необходимо постоянно изменять цели в структуре организационных систем.
Изменение целей в структуре ОС должны базироваться на основе следующих принципов:
1) принцип иерархичности структуры. Этот принцип позволяет проводить анализ структуры и выделять: задачи, подцели первого, второго и других уровней по подчиненности и т.д. ЛПР представляет функционирование ОС, как показывают результаты исследований, более четко в виде иерархической структуры
2) принцип альтернатив. При решении сложных задач, включающих несколько компонентов, ЛПР использует один из трех методов:
а) одновременное достижение цели;
б) метод очередности, когда цели достигаются последовательно во времени;
в) размещение целей, заключающееся в поочередном их достижении с изменением очередности в зависимости от складывающихся обстоятельств;
3) принцип иерархичности альтернативных способов действий.
Для упрощения выбора множеств альтернатив ЛПР может последовательно разделять на классы и подклассы задачи.
Цели, подцели и иное путем использования на каждом шаге процесса деления некоторых определяющих признаков. В результате образуется иерархическая структура альтернатив. Такой прием позволяет представить задачи, цели, подцели и иное, имеющие относительно малую размерность и поэтому более приспособленные для решения на электронной вычислительной машине;
4) принцип редукции при переходе от сложного к простому. Проявляется в рассмотрении только ограниченного числа альтернативных решений и исключении остальных;
5) принцип конкретизации. Заключается в использовании при решении задачи только информации, заданной в явном виде. Использование такого принципа оправдано в условиях острого дефицита времени, не позволяющего осуществить ассоциативный поиск в БЗ (база знаний) для ЛПР.
Определение структуры ОС производится, как правило, на основе анкетирования и экспертного анализа взаимодействия элементов в структуры.
Анкетирование должно производиться с выявлением следующей информации:
1) частота управленческих решений;
2) описание механизма принятия управленческих решений руководителем для подчиненных;
3) степень участия руководителя в принятии управленческих решений подчиненными.
Такой тип анкетирования позволит определять структуру рассматриваемых систем.
Такую структуру можно представить в виде множества, состоящего из элементов структуры и множества управляющих связей.
В случае, если граф из данных множеств непредставим в иерархическом виде, его необходимо сопоставить с иерархическим представлением целей и привести к иерархическому виду.
Разбиение сложной системы (СС) на иерархическую структуру невозможно осуществить без применения системного подхода.
Предположим, что СС представлена в виде графа без контуров G(V, E) (V – являются вершинами графа СС, E – являются дугами этого графа).
Управляющие связи в рассматриваемой сложной системе описываются следующими элементами (r1, r2) Î E, если элемент r2 управляется r1).
С помощью рассматриваемого графа G точно описать сложную систему Sa невозможно. Поэтому выбираем граф G, соответствующий рассматриваемой структуре СС Sa.
Представление СС в виде вершин V= (v1, v2, …, vn) на основе попарно непересекающегося множества VkÍV в дальнейшем будем называть сложной иерархической структурой (СИС) [1,3], если не существует дуг (r1, r2) ÎE таких, что (r1ÎVk, r2ÎVj, k>j).
Представление СС в виде множества вершин V= (v1, v2, …, vn) в СИС реализуется на основе разных подходов в зависимости от цели, которую преследует данное представление в соответствии с целями (Цa) и задачами {![]() }, j=1, …, ma, рассматриваемыми в данной системе [4, 5].
}, j=1, …, ma, рассматриваемыми в данной системе [4, 5].
Необходимо, чтобы было соответствие графа G, который описывает СС, относительно множества решаемых задач {![]() }, j=1, …, ma и объема выполняемых работ (ОВР) в каждом элементе рассматриваемой сложной иерархической структуры.
}, j=1, …, ma и объема выполняемых работ (ОВР) в каждом элементе рассматриваемой сложной иерархической структуры.
Определим относительный ОВР (ООВР) ![]() для каждого элемента ({
для каждого элемента ({![]() }, j=1, …, ma)в виде
}, j=1, …, ma)в виде
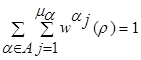 (1)
(1)
Поэтому распределение данных задач получим в следующем виде:
W(r)=W1(r), W2(r), …, WL(r) (2)
где
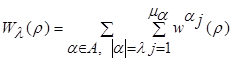 (3)
(3)
Wl(r) - ООВР для элемента r в соответствии целям l-го.
Эта задача сводится к максимизации функционала СИС s =(V1, V2, …, VL) для графа G(V, E) с:
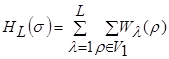 (4)
(4)
Функционал будет максимальным при разбиении s*=![]() в виде:
в виде:
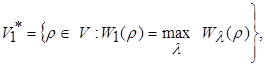 (5)
(5)
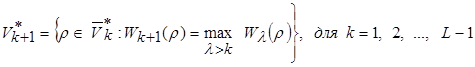 (6)
(6)
,где ![]()
Предположим, что для СИС вида s существует IL(G) – множество всех представлений графа G в виде:
![]() (7)
(7)
Что соответствует функциональному уравнению Беллмана [2]:
![]() (8)
(8)
,где Θ(Х) для любого подмножества XÍVсуществует множество вершин графа G.
Разберем варианты представления ориентированного графа на СИС, которые можно представить в виде иерархической структуры s, с помощью нее возможно определить максимум функционала (4).
Предположим, что в графе G существует множество IL(G), где L – уровни иерархий, со следующим отношением s1£s2, в том случае, если выполняется следующее условие:
![]() (9)
(9)
, где: k= 1,2, ..., L-1
Для этого случая для любого подмножества множества IL(G) возможно определить точные нижнюю (s/) и верхнюю границу (s//) ,которые будут определяться выражениями:
![]() (10)
(10)
Следовательно, справедливо выражение:
H(s1)+H(s2)=H(min {s1, s2})+H(max {s1, s2}). (11)
где: для любых s1, s2ÎIL(G).
Преобразуем 11 в вид:
H(min {s1, s2})+H(max {s1, s2})=H(s1)=H(s2). (12)
Следовательно, что подмножества IL0 (G) будут оптимальными иерархиями и множество IL0 (G) представимы в виде решетки.
Следовательно, возможно построить алгоритм определения (s/) для множества всех оптимальных иерархий (s*).
1. Первым приближением определим иерархию s0=IL(G)
s*<s0=IL(G). (13)
2. Если сформирована иерархия sk, тогда на основе оператора А:sk+1=A(sk) с учетом sk+1
s*£A (sk) £sk, (14)
причем, если s*<sk, тоsk+1<sk
3. Если sk+1=sk, тогда конец разбиению иначе переход к пункту 2.
Следовательно, функционал будет возрастать:
![]() (15)
(15)
Поэтому справедливо выражение:
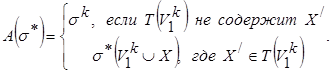 (16)
(16)
После того как ориентированный граф без контуров определен в СИС, необходимо сопоставить его с целями Цa.
Функционирование элементов в СС определяется подцелями ЦbÍЦa. [2]. Относительная загруженность всех элементов СС r определяется выражением:
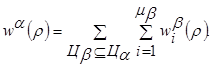 (17)
(17)
Предположим, что nl — это количество задач, решаемых СС, на l-м уровне дерева целей. Граф G(V, E) приведем в соответствие с задачами СС в соответствии с разбиением V на СИС s=(V1,V2, …, VL).
Максимум функционала можно найти по не связанным между собой дугам eÎV для несвязанных Va1, Va2, …, VaVa, на основе следующего выражения:
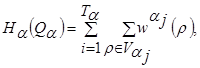 (18)
(18)
где l= 2, 3, …, L иaÎА, ïaï=l-1 разбиения Qa множеств![]() .
.
![]() определяется как:
определяется как:
![]() ; если Va, где ïaï>1, определенно, то
; если Va, где ïaï>1, определенно, то![]() .
.
Эта задача определяется для графа G(V, E) определением векторной функции W(r)=(w1(r), w2(r), …, wn(r)) на представлении Q=(V1, …, Vn) в виде не связанных между собой дуг eÎV подмножества Vi, i, …, n, которая позволит максимизировать функционал [6].
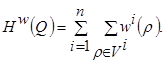 (19)
(19)
Максимум функционала определяется в виде представления V подмножествами V1, V2, …, Vm. Значение wi(Vj) для![]() определяется выражением:
определяется выражением:
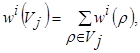 (20)
(20)
Последовательно для i=1, 2, …, n выбираем для Vj компоненты на основе выражения:
![]() (21)
(21)
Поэтому представление Q будет являться решением задачи.
Рецензенты:
Десятов Д.Б. д.т.н., профессор, профессор кафедры технических комплексов охраны и связи Воронежского института ФСИН России, г. Воронеж;
Душкин А.В. д.т.н., начальник кафедры управления и информационно-технического обеспечения Воронежского института ФСИН России, г. Воронеж.



