Цель исследования
Целью данной работы является исследование устойчивости стационарного режима работы вибрационного грохота на комбинационном параметрическом резонансе.
Материалы и методы
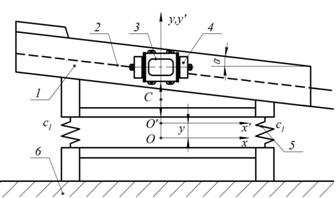
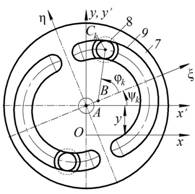
Важнейшим вопросом динамики резонансного грохота является исследование устойчивости стационарного режима, поскольку резонансные машины чувствительны к изменению технологической нагрузки [6]. Рассмотрим устойчивость стационарного режима динамической модели грохота, предложенной в [7] и представленной на рисунке 1. Параметрические вибровозбудители 3 жестко закрепляются на корпусе грохота 1 массой M0. Основным узлом параметрического вибровозбудителя является роторно-маятниковая система. Механизм инерционного элемента (ИЭ) вибровозбудителя выполнен по патенту № 2410167 [9]. Грохот связан упругими элементами 5 с основанием, которое жестко закреплено на фундаменте 6 (рис. 1).
а б
Рис. 1. Динамическая модель вибрационного грохота
При исследовании устойчивости движения целесообразно наблюдать не поведение обобщенных координат системы в возмущенном движении, а только их возмущения (вариации) от координат, которые они имели в невозмущенном движении.
Будем исходить из дифференциальных
уравнений движения, полученных в [7]. Если ввести безразмерное время ![]() ,
безразмерные координаты
,
безразмерные координаты ![]() и удержать в указанных уравнениях
величины до третьего порядка относительно координат и их производных, то математическую
модель вибрационного грохота с параметрическими вибровозбудителями можно
записать в следующем виде:
и удержать в указанных уравнениях
величины до третьего порядка относительно координат и их производных, то математическую
модель вибрационного грохота с параметрическими вибровозбудителями можно
записать в следующем виде:
![]()
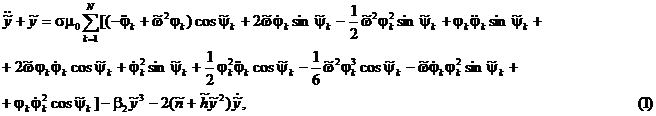 где
где
![]() ,
, ![]()
![]()
![]() безразмерные
коэффициенты линейного демпфирования,
безразмерные
коэффициенты линейного демпфирования, ![]() безразмерные коэффициенты нелинейного
демпфирования,
безразмерные коэффициенты нелинейного
демпфирования, ![]() - коэффициент
нелинейности упругих восстанавливающих сил,
- коэффициент
нелинейности упругих восстанавливающих сил, ![]() безразмерная
частота параметрического возбуждения,
безразмерная
частота параметрического возбуждения, ![]()
![]() ,
,
![]()
![]() ,
N
– количество тел качения,
,
N
– количество тел качения, ![]() общая масса системы,
общая масса системы, ![]() –
количество дисков, JB – момент инерции тела качения
относительно оси обкатки,
–
количество дисков, JB – момент инерции тела качения
относительно оси обкатки, ![]()
![]()
![]() ,
,![]() ,
,
![]() – собственные частоты тел качения и
рабочего органа. Точка обозначает дифференцирование по τ.
– собственные частоты тел качения и
рабочего органа. Точка обозначает дифференцирование по τ.
Решение уравнений (1) будем искать в виде:
![]() , k=1,2,…,N,
, k=1,2,…,N,![]() .
(2)
.
(2)
Принимая A, Ak, θ, θk за новые медленные переменные и выполняя стандартную процедуру метода усреднения [5], после преобразований получим усредненные уравнения первого приближения.
![]()
![]()
![]() (3)
(3)
![]() k=1,2,.., N,
k=1,2,.., N,
Стационарный режим работы вибрационной
машины получается как особые точки системы (3) при равных нулю правых частях,
т. е. ![]() Поскольку осцилляторы качения
идентичны, то Ak=A0, k=1, 2,…,N. Также должно выполняться условие
Поскольку осцилляторы качения
идентичны, то Ak=A0, k=1, 2,…,N. Также должно выполняться условие ![]() k=1,2,…,N.
k=1,2,…,N.
В результате приходим к системе алгебраических уравнений относительно неизвестных стационарных амплитуд A0, A, фазы θ и частот генерации ω1 и ω2
![]()
![]() (4)
(4)
![]()
![]()
Исследуем устойчивость особых точек, соответствующих стационарному режиму колебаний, воспользовавшись методом, предложенным в [8]. Для этого составим уравнения в вариациях:
![]() (5)
(5)
где
![]() – коэффициенты уравнений первого
приближения (матрица Якоби),
– коэффициенты уравнений первого
приближения (матрица Якоби), ![]() – вариация (отклонение) величины qj(t).
– вариация (отклонение) величины qj(t).
Устойчивость положения равновесия определяется знаками действительных частей собственных значений матрицы Якоби. Чтобы найти собственные значения p, необходимо решить характеристическое уравнение алгебраического вида:
![]() (6)
(6)
z – порядок системы.
Вычисления
корней такого уравнения может представлять значительные трудности, особенно,
если ![]() поэтому большое значение имеют методы,
позволяющие, не решая само характеристическое уравнение, установить
устойчивость системы. Составим матрицу Якоби, вычисляя частных производных
системы уравнений первого приближения (3).
поэтому большое значение имеют методы,
позволяющие, не решая само характеристическое уравнение, установить
устойчивость системы. Составим матрицу Якоби, вычисляя частных производных
системы уравнений первого приближения (3).
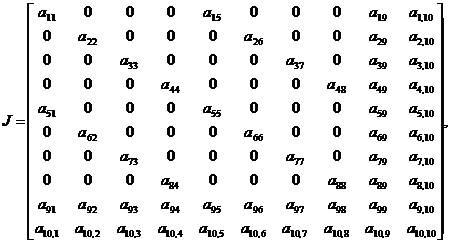 (7)
(7)
где
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Выделим в матрице одинаковые коэффициенты и заменим индексы коэффициентов младшими из них. Тогда уравнения возмущенного движения примут вид:
![]()
![]()
![]()
![]()
![]()
![]() (8)
(8)
![]()
![]()
![]()
![]()
Полученная система из десяти дифференциальных уравнений первого порядка имеет линейно зависимые столбцы (второй и четвертый), что значительно усложняет исследование устойчивости, поскольку определитель матрицы будет равняться нулю. Выход из данной ситуации предложен в работе [8]. Для этого необходимо разделить систему (8) на три системы. Первые две системы получатся путем попарного вычитания и сложения первых восьми уравнений возмущенного движения, а третья система будет состоять из двух последних уравнений системы (8).
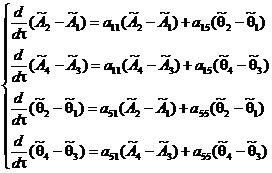 (9)
(9)
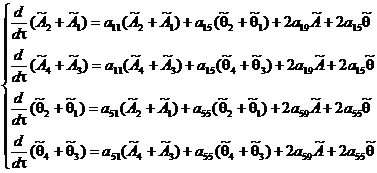 (10)
(10)
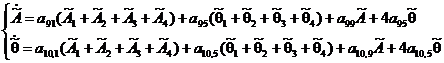 (11)
(11)
Систему уравнений (9) можно разложить на две замкнутые независимые подсистемы для разностей возмущений, которые можно исследовать на устойчивость:
 (9а)
(9а) 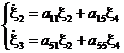 (9б)
(9б)
где
![]()
![]()
![]()
![]() В
уравнениях (10) и (11) произведем замену переменных
В
уравнениях (10) и (11) произведем замену переменных ![]()
![]()
![]()
![]() затем попарно вычтем и сложим уравнения
системы (10), в результате получим одну систему для разностей возмущений (12) и
систему (13) для суммы возмущений с добавкой уравнений системы (11).
затем попарно вычтем и сложим уравнения
системы (10), в результате получим одну систему для разностей возмущений (12) и
систему (13) для суммы возмущений с добавкой уравнений системы (11).
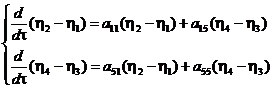 (12)
(12)
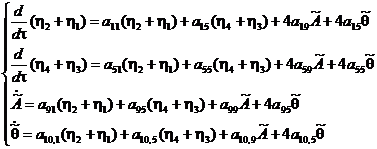 (13)
(13)
Таким
образом, система (10), (11) распадается на две замкнутые независимые подсистемы
(12) и (13), состоящие из двух и четырех уравнений соответственно. Проведем
замену переменных ![]()
![]()
![]()
![]() ,
и уравнения (12) и (13) примут вид:
,
и уравнения (12) и (13) примут вид:
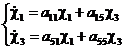 (14)
(14) (15)
(15)
В уравнениях (15) второй и четвертый столбцы зависимы, поэтому для дальнейшего исследования необходимо сложить эти столбцы, а затем мы можем сложить вторую и четвертую строки. В результате получим систему из трех уравнений без линейной зависимости:
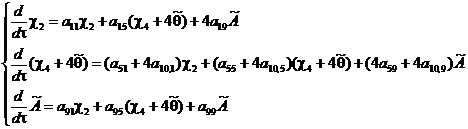 (15а)
(15а)
Приведем
полученную систему к более компактному виду, заменив выражение ![]() переменной
переменной
![]() :
:
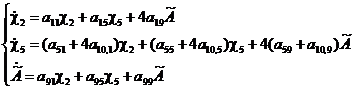 (15б)
(15б)
В результате системы уравнений (9а), (9б), (14) и (15б) можно исследовать на устойчивость, после чего можно делать вывод об устойчивости системы в целом.
В соответствии с критерием Рауса-Гурвица можно определить устойчивость положения равновесия для систем (9а), (9б) и (14). Для системы 2-го порядка условие устойчивости имеет вид: a0>0, a1>0, a2>0, т. е. все коэффициенты характеристического уравнения должны быть положительными. Поскольку коэффициенты уравнений (9а), (9б) и (14) равны, можно составить одно характеристическое уравнение второго порядка для этих систем:
![]() (16)
(16)
где
![]()
![]()
![]()
Для исследования устойчивости системы (15б) снова воспользуемся критерием Рауса-Гурвица и составим характеристическое уравнение третьего порядка в соответствии с (6), которое примет вид:
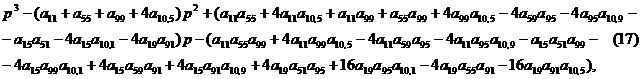 где
где ![]()
![]()
![]()
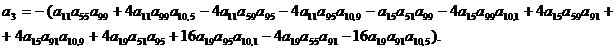
В
соответствии с критерием Рауса-Гурвица для системы 3-го порядка условие
устойчивости имеет вид: a0>0, a1>0, a2>0, a3>0, т. е. все коэффициенты
характеристического уравнения должны быть положительными и дополнительное
условие ![]()
Результаты и их обсуждение
Проведем анализ полученных результатов
на амплитудно-частотной характеристике рабочего органа грохота при различных
параметрах системы. На рисунке 2 показаны резонансная кривая 1, соответствующую
комбинационному резонансу, при настройке ε=0.02, n=0.25,
![]()
![]()
![]() β1=1/6,
β2=0,15, и резонансная кривая 2, соответствующую настройке
ε=0.02, n=0.25,
β1=1/6,
β2=0,15, и резонансная кривая 2, соответствующую настройке
ε=0.02, n=0.25, ![]() ,
,
![]() ,
, ![]() β1=1/6,
β2=0.
β1=1/6,
β2=0.
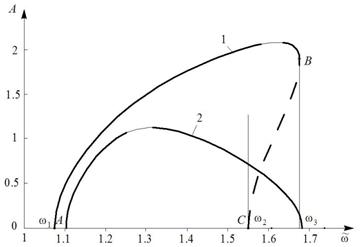
Рис. 2. АЧХ рабочего органа. Границы устойчивости
Все коэффициенты характеристического уравнения (16) для резонансной кривой 2 получились положительными, что говорит об устойчивости положения равновесия резонансного режима работы. Для кривой 1 на участке от А до В коэффициенты характеристического уравнения имеют положительные значения, а на участке от В до С – отрицательные значения. Следовательно, на участке АВ положение равновесия устойчиво, а на участке ВС, отмеченном пунктирной линией, – неустойчиво. Тривиальное решение от ω1 до ω2 неустойчиво.
После
определения коэффициентов характеристического уравнения (17) и проверки
дополнительного условия устойчивости можно сделать вывод, что кривая 2 является
устойчивой на всем участке. Все точки левой ветви резонансной кривой 1 (от А до В)
оказались устойчивыми. Стационарное решение на интервале ![]() является
многозначным. Из трех возможных значений амплитуды установившихся колебаний
устойчивым колебаниям соответствует тривиальное решение (колебания с нулевой
амплитудой) и нетривиальное решение с наибольшей амплитудой, а неустойчивым – с
наименьшей амплитудой (участок кривой ВС).
Сплошными линиями показаны асимптотически устойчивые решения, а штриховыми –
неустойчивые.
является
многозначным. Из трех возможных значений амплитуды установившихся колебаний
устойчивым колебаниям соответствует тривиальное решение (колебания с нулевой
амплитудой) и нетривиальное решение с наибольшей амплитудой, а неустойчивым – с
наименьшей амплитудой (участок кривой ВС).
Сплошными линиями показаны асимптотически устойчивые решения, а штриховыми –
неустойчивые.
Обобщая результаты, полученные при исследовании устойчивости систем уравнений (9а), (9б), (14) и (15б), можно сделать вывод, что в целом система является устойчивой.
Заключение
Точка ω=ω1 является точкой бифуркации, при переходе которой положение равновесия теряет устойчивость и возникает неравновесное состояние – периодические колебания. Этот вид потери устойчивости называется мягкой потерей устойчивости, поскольку устанавливающийся колебательный режим при малой закритичности ε*=ω-ω1 (отличие параметра ω от критического значения ω1) мало отличается от равновесия. При переходе ε* через нуль устойчивый фокус становится неустойчивым, и рождается устойчивый предельный цикл малой амплитуды, что соответствует динамической бифуркации Андронова-Хопфа.
Проделанный анализ показал, что стационарный режим работы вибрационного грохота с параметрическими вибровозбудителями является устойчивым. Полученные результаты подтверждаются проведенными экспериментами, что говорит о достоверности предложенного метода.
Рецензенты:
Панов А. Ю., д.т.н., заведующий кафедрой «Теоретическая и прикладная механика», ФГБОУ ВПО «Нижегородский государственный технический университет им. Р.Е. Алексеева», г. Нижний Новгород;
Кретинин О.В., д.т.н., кафедра «Автоматизация машиностроения», ФГБОУ ВПО «Нижегородский государственный технический университет им. Р.Е. Алексеева», г. Нижний Новгород.



