В практике преподавания естественнонаучных и инженерных дисциплин математические модели, исследуемые в учебных задачах, достаточно объемны и сложны, а их «ручная» математическая обработка требует больших затрат учебного времени, отводимого на аудиторную и самостоятельную работу студента.
С целью оптимизации использования учебного времени студентов, затрачиваемого на обработку математических моделей вычислительного эксперимента, необходимо научить
их использованию возможностей современных программно-аппаратных сетевых ресурсов, чтобы на их основе минимизировать временные затраты на вычислительные операции.
В учебном процессе естественнонаучных и инженерных дисциплин нет избытка времени, позволяющего изучать прикладные программы со сложным интерфейсом. В этой связи особое внимание заслуживает пакет Wolfram Mathematica – мощная система компьютерной алгебры с достаточно удобным, интуитивно понятным и простым в освоении интерфейсом.
Учебные учреждения всего мира используют пакет Wolfram Mathematica в университетском образовании. Однако сразу следует отметить высокую стоимость пакета Wolfram Mathematica, что делает весьма проблематичным его использование российскими студентами. Потому в нашей работе исследуются возможности применения в учебном вычислительном эксперименте свободных Интернет-ресурсов:
-
свободная онлайн-версия пакета компьютерной алгебры Wolfram Mathematica, Интернет-адрес ресурса [7];
-
онлайн-вычислитель WolframAlpha, Интернет-адрес ресурса [6].
Пример решения практико-ориентированной учебной технической задачи, с использованием, для решения дифференциального уравнения, свободной онлайн-версии компьютерной алгебры Wolfram Mathematica
Задача. На глубокой и спокойной воде осуществляется разгон судна от нулевой скорости (относительно воды) до установившегося ее значения, соответствующего заданному положению телеграфа. Считая, что упор винта (сила, с которой винт толкает судно) равен
P = 465 кН, в режиме разгона судна остается постоянным. Сопротивление воды пропорционально квадрату скорости судна. Определить зависимость скорости движения судна в зависимости от времени, найти установившуюся скорость движения судна (ответ выразить в узлах; 1 узел = 1852 м/ч ≈ 0,51 м/с).
Коэффициент сопротивления движению K = 11280 кг/м. Водоизмещение судна
T = 7500 т, масса судна при прямолинейном движении M ≈ 1,1T (с учетом присоединенных масс воды – при своем движении судно перемещает вместе с собой некоторую часть воды, взаимодействующей с корпусом судна).
Решение. Решая эту задачу, студенты и курсанты исследуют физику процесса и, применив законы динамики, составляют две математические модели движения судна.
Первая модель характеризует динамику изменения скорости судна. Она выражается дифференциальным уравнением:
![]() (1)
(1)
решение которого «ручным» способом – задача трудоемкая.
Вторая модель
P – Kυ2 = 0,
характеризует движение судна с установившейся скоростью. Из второй модели установившаяся скорость движения находится простым вычислением:
![]()
Решение задачи средствами онлайн-версии пакета Wolfram Mathematica.
После регистрации на странице WOLFRAM CLOUD онлайн-версии пакета Wolfram Mathematica [7] открываем ячейку ввода программного кода, в которую вводим математическую модель исследуемого физического процесса (1), дополненную начальными условиями (разгон судна осуществляется от нулевой скорости):
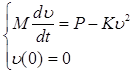 (2)
(2)
Для решения этого уравнения средствами онлайн-версии пакета Wolfram Mathematica используем команду DSolve[ ], параметрами которой и является математическая модель (2):
DSolve[{Vx'[t] + (K/M)*(Vx[t])^2 == P/M, Vx[0] == 0}, Vx[t], t]
На рис. 1 показан скриншот окна программы Wolfram Mathematica после запуска режима «Исчисление» кода, записанного в ячейку ввода In[1]. Запуск этого режима производится нажатием комбинации клавиш «Shift + Enter» на основной клавиатуре, или клавиши «Enter» – на цифровой клавиатуре. После исполнения команды DSolve[ ], в рабочем окне Wolfram Mathematica открылась еще одна ячейка – ячейка вывода результата Out[1].

Рис. 1. Окно программы Wolfram Mathematica после запуска режима «Исчисление»
Числовые значения коэффициентов K, M, P в командном коде, введенном в ячейку ввода, предварительно нами не были объявлены, поэтому решение, полученное после исполнения команды DSolve[ ], имеет символьный вид
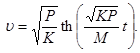
С учетом
![]() ,
,
искомое нами символьное решение имеет вид:
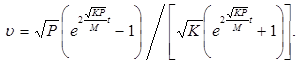 (3)
(3)
Создадим еще одну ячейку ввода In[2], в которой, перед командой DSolve[ ], присвоим соответствующие числовые значения коэффициентам K, M, P. После исполнения кода, записанного
в ячейке In[2], в ячейке вывода результата Out[3] появляется результат с числовыми коэффициентами.
Результат, полученный в ячейке Out[3] (см. рис.2), нам привычнее видеть с символьным отображением основания натурального логарифма. Заменив числовое значение 2,71828 символом e, получим искомое решение исследуемого нами дифференциального уравнения:
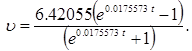 (4)
(4)

Рис. 2. Окно программы Wolfram Mathematica после исчисления модифицированного кода
Создадим еще одну ячейку ввода In[4], в которую скопируем программный код
из предыдущей ячейки ввода In[2], дополнив его командой Plot[ ] со следующими параметрами:
Plot[ Evaluate[Vx[t]/.V,{t,0,500}],GridLines → Automatic, Frame → True]
Вид ячейки ввода In[4] с модифицированным кодом и результат исполнения этого кода показаны на рис. 3.
В ячейке вывода Out[5] мы видим результат, уже известный нам из ячейки вывода Out[3]. В ячейке вывода Out[6] построен график изменения скорости судна в функции времени.
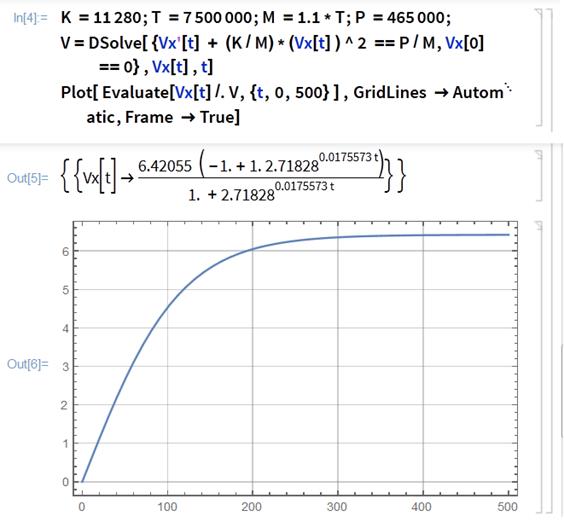
Рис. 3. Окно программы Wolfram Mathematica с ячейкой вывода графического результата
Конечно, онлайн-версия пакета Wolfram Mathematica не дает пользователю доступа
к значительной части интерфейса своего коммерческого варианта, однако и в таком виде она может быть успешно использована в учебном вычислительном эксперименте дисциплин естественно-технического направления.
Пример решения дифференциального уравнения средствами свободного онлайн-вычислителя WolframAlpha
Для решения рассмотренной выше задачи средствами свободного онлайн-вычислителя WolframAlpha, выйдем на Интернет-сайт этой программы [6].
Для символьного решения исследуемого дифференциального уравнения вводим его практически в стандартном для математиков виде в ячейку ввода:
{M*V(t)' + k*V(t)^2 - P=0, V(0)=0}
Вид ячейки ввода с введенным выражением и результат исчисления, полученный после клика виртуальной кнопки «=», расположенной в ячейке ввода справа, показан рис. 4
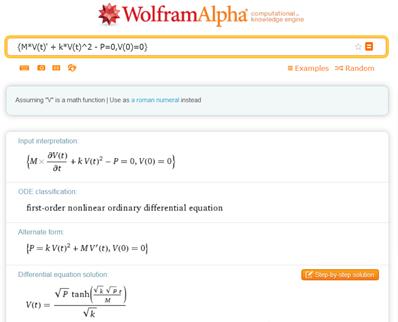
Рис. 4. Окно программы WolframAlpha с результатом символьного решения
Если в ячейку ввода ввести математическую модель с числовыми значениями коэффициентов,
{1.1*7500000*V(t)' + 11280*V(t)^2 - 465000=0,V(0)=0},
то полученный результат будет аналогичен тому, что мы получили, используя пакет Wolfram Mathematica, см. рис. 5
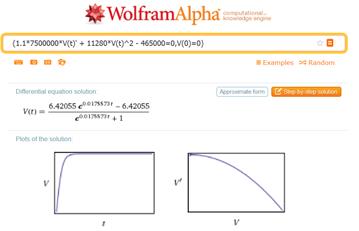
Рис. 5. Окно программы WolframAlpha с результатом числового решения и графиками
Заключение
Продуктивное усвоение студентами и курсантами предметного материала дисциплины
на основе использования современных программно-аппаратных и сетевых ресурсов в учебном вычислительном эксперименте определяет мотивационный аспект, формирует познавательный интерес и ценностное отношение к профессиональным знаниям.
Рецензенты:
Власов А.Б., д.т.н., профессор, заместитель начальника по научной работе Морской академии Мурманского государственного технического университета, г. Мурманск;
Морозов Н.Н., д.т.н., профессор, заведующий кафедрой общей и прикладной физики Мурманского государственного технического университета, г. Мурманск.



