Введение
Конкуренция на рынке лесопромышленного производства неуклонно растет с каждым годом. Это способствует ужесточению требований к техническому состоянию технологического оборудования, в частности гидроманипуляторов. Повышаются требования к надежности, производительности, себестоимости манипуляторного оборудования. Одним из факторов, определяющим производительность машины манипуляторного типа, является время протекания переходных процессов [7]. Для определения времени переходных процессов надо получить зависимости ускорений звеньев от параметров манипулятора при погрузке или разгрузке, что удобнее всего сделать с помощью уравнений Лагранжа. В процессе составления уравнений Лагранжа следует найти обобщенные силы на каждом возможном перемещении механической системы. Кинематические схемы были рассмотрены ранее [1, 2, 3, 7] без учета либо пространственного движения, либо движения телескопической части. В данной работе эти виды движения учтены.
Цель исследования
Изучение динамических процессов погрузки-разгрузки сортиментов машинами манипуляторного типа с учетом четырех степеней свободы, определение обобщенных сил и кинетической энергии системы.
Задачи исследования
-
Создание модели гидроманипулятора в виде кинематической схемы.
-
Определение числа степеней свободы и выбор обобщенных координат.
-
Расчет обобщенных сил и кинетической энергии.
Создание модели гидроманипулятора в виде кинематической схемы.
В настоящей работе мы предлагаем схему шарнирно-сочлененного манипулятора с телескопической рукоятью (комбинированная схема на основе схем в работах [2,3,7]), представленную на рисунке 1.
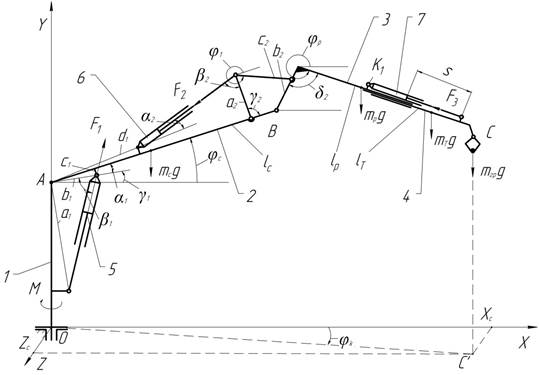
Рис.1. Кинематическая схема гидравлического манипулятора: 1 – колонна; 2 – стрела; 3 – рукоять; 4 – телескопическая секция; 5 - гидроцилиндр привода стрелы; 6 – гидроцилиндр привода рукояти; 7 – гидроцилиндр привода телескопического удлинителя
В качестве первого приближения примем, что центры масс звеньев манипулятора (стрела, рукоять, телескопический удлинитель) находятся на осях этих звеньев в центрах соответствующих звеньев.
На схеме приведены следующие обозначения:
mгр – масса груза с грейфером и ротатором;
mс, – масса стрелы с гидроцилиндром и механизмом привода рукояти;
mр – масса рукояти с гидроцилиндром привода телескопического удлинителя;
mт – масса телескопического удлинителя рукояти;
F1, F2, F3 – усилия на поршне в штоковой полости гидроцилиндров привода стрелы, рукояти, телескопического удлинителя, соответственно;
φк – угол поворота колонны вокруг OY;
φс – угол между стрелой и ОХ;
![]()
φр - угол между рукоятью и ОХ;
a1 , d1 , b1 ,c1 ,α1 - заданные параметры механизма подъема стрелы [1,6];
a2 , b2 ,c2 , δ2 - заданные параметры механизма привода рукояти;
α2 - текущее значение угла между осью гидроцилиндра привода рукояти и прямой d1;
γ2 - текущее значение угла между осью звена a2 и осью стрелы;
φ1 - текущее значение угла между осью звена c2 и прямой параллельной оси стрелы;
φр - текущее значение угла между осью рукояти и оси ОХ;
s - координата точки приложения силы F3, действующей на шток гидроцилиндра привода телескопической секции рукояти, относительно точки К1;
lс - длина стрелы;
lр - длина рукояти;
lт - длина телескопического удлинителя;
β1 - текущее значение угла между осью гидроцилиндра подъема стрелы и прямой b1;
β2 - текущее значение угла между осью гидроцилиндра привода рукояти и звеном a2;
Определение числа степеней свободы и выбор обобщенных координат.
Для описания динамического процесса погрузки-разгрузки составим дифференциальные уравнения методом уравнения Лагранжа 2-го рода. Определим соответствующие обобщенные силы на каждом возможном перемещении.
Определим независимые обобщенные координаты ![]() число которых равно числу степеней свободы. Механизм имеет 4 степени подвижности. Удобно выбрать в качестве обобщенных координат следующие переменные:
число которых равно числу степеней свободы. Механизм имеет 4 степени подвижности. Удобно выбрать в качестве обобщенных координат следующие переменные:
- ![]() - угол поворота колонны относительно оси Y;
- угол поворота колонны относительно оси Y;
- ![]() - угол поворота стрелы вокруг т. А;
- угол поворота стрелы вокруг т. А;
- ![]() - угол поворота рукояти вокруг т. В;
- угол поворота рукояти вокруг т. В;
- ![]() – координата точки приложения силы F3, действующей на шток гидроцилиндра привода телескопической секции рукояти, относительно точки К1.
– координата точки приложения силы F3, действующей на шток гидроцилиндра привода телескопической секции рукояти, относительно точки К1.
Записываем уравнения Лагранжа II рода:
![]() ; (i=1..4) (1)
; (i=1..4) (1)
где Т – кинетическая энергия системы, Qi – обобщенные силы
Расчет обобщенных сил и кинетической энергии.
Вычислим сумму элементарных работ моментов и сил на соответствующих приращениях обобщенных координат.
При ![]() ,
, ![]() ,
, ![]() ,
,![]() вращается только колонна вокруг оси Y, все остальные звенья (стрела, рукоять, телескопический удлинитель) неподвижны. Силы F1, F2, F3 принадлежат вертикальной плоскости и не совершают работу на заданном перемещении. Сумма элементарных работ
вращается только колонна вокруг оси Y, все остальные звенья (стрела, рукоять, телескопический удлинитель) неподвижны. Силы F1, F2, F3 принадлежат вертикальной плоскости и не совершают работу на заданном перемещении. Сумма элементарных работ ![]() всех активных сил и моментов на данном возможном перемещении будет равна:
всех активных сил и моментов на данном возможном перемещении будет равна:
![]() , (2)
, (2)
где М – момент от гидроцилиндров поворота колонны.
Обобщенная сила на заданном возможном перемещении из равенства (2) равна:
![]() . (3)
. (3)
При ![]() ,
, ![]() ,
, ![]() ,
, ![]() вращается только стрела, остальные звенья неподвижны. На данном возможном перемещении будут работать и все силы тяжести и силы Fi. Сумма элементарных работ
вращается только стрела, остальные звенья неподвижны. На данном возможном перемещении будут работать и все силы тяжести и силы Fi. Сумма элементарных работ ![]() на данном возможном перемещении равна:
на данном возможном перемещении равна:
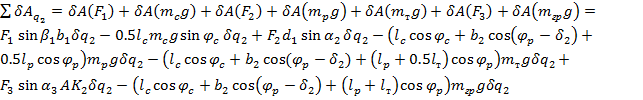 , (4)
, (4)
где α3 – это угол между отрезками К1К2 и АК2.
Знак работы определяется косинусом угла между вектором силы и перемещением. Так как ![]() направлена против часовой стрелки, работы всех сил тяжести будут отрицательны. Зная это в соотношении (4) для элементарной работы
направлена против часовой стрелки, работы всех сил тяжести будут отрицательны. Зная это в соотношении (4) для элементарной работы ![]() считаем по модулю.
считаем по модулю.
Обобщенная сила на заданном возможном перемещении равна:
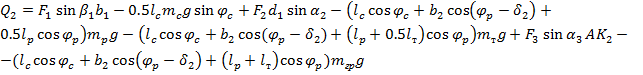 (5)
(5)
При ![]() ,
, ![]() ,
, ![]() ,
, ![]() сумма элементарных работ
сумма элементарных работ ![]() всех активных сил на данном возможном перемещении равна:
всех активных сил на данном возможном перемещении равна:
![]() (6)
(6)
Следует более подробно рассмотреть вывод формулы для элементарной работы ![]() . Для вычисления элементарной работы силы F2 рассмотрим более детально рычажный механизм привода рукояти (см. рис. 2). Обозначим вершины четырехзвенника, образованного рычажным механизмом как B, D, K, E.
. Для вычисления элементарной работы силы F2 рассмотрим более детально рычажный механизм привода рукояти (см. рис. 2). Обозначим вершины четырехзвенника, образованного рычажным механизмом как B, D, K, E.
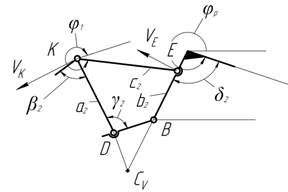
Рис.2. Схема механизма привода рукояти:
VK – скорость т.К; VE – скорость т.Е; СV – мгновенный центр скоростей звена КЕ.
На данном перемещении звенья BE и DK совершают вращательное движение вокруг точек В и D, соответственно. Звено КЕ совершает плоско - параллельное движение. Звено DB неподвижно. Чтобы определить работу силы F2, приложенной в точке К, необходимо выразить перемещение точки К через ![]() . Воспользуемся теоремой о существовании мгновенного центра скоростей (СV) чтобы сначала получить связь между скоростями точек К и Е. Точки К и Е это шарнирные сочленения звена КЕ со звеньями DK и ВЕ, которые совершают простое вращательное движение на заданном перемещении. В этом случае векторы скоростей VK и VE этих точек будут перпендикулярны звеньям DK и ВЕ, и мгновенный центр скоростей звена КЕ будет находиться на пересечении продолжений этих звеньев.
. Воспользуемся теоремой о существовании мгновенного центра скоростей (СV) чтобы сначала получить связь между скоростями точек К и Е. Точки К и Е это шарнирные сочленения звена КЕ со звеньями DK и ВЕ, которые совершают простое вращательное движение на заданном перемещении. В этом случае векторы скоростей VK и VE этих точек будут перпендикулярны звеньям DK и ВЕ, и мгновенный центр скоростей звена КЕ будет находиться на пересечении продолжений этих звеньев.
Получим треугольник КCVЕ. Запишем уравнение связи при плоском движении:
![]() , ( 7)
, ( 7)
где ![]() – это угловая скорость звена КЕ (с2 ).
– это угловая скорость звена КЕ (с2 ).
Из уравнения связи (7) получим связь между скоростями:
![]() , (8)
, (8)
Здесь соотношение ![]() – это связь между радиусами вращения точек относительно СV.
– это связь между радиусами вращения точек относительно СV.
В треугольнике КCVЕ углы в вершинах К и Е определим через выбранные углы положения звеньев. По теореме синусов получаем:
![]()
![]() (9)
(9)
Подставив выражение 9 в формулу 8 получим скорость точки К
![]() (10)
(10)
При плоско-параллельном движении звена КЕ связь между перемещениями ![]() и
и ![]() , точек К и Е будет такой же как и между скоростями VK и VE соответствующих точек. Перемещение
, точек К и Е будет такой же как и между скоростями VK и VE соответствующих точек. Перемещение ![]() – это произведение радиуса вращения этой точки (в данном случае радиус – это сторона звена DK=a2) на угол поворота этого радиуса (элементарное приращение угла):
– это произведение радиуса вращения этой точки (в данном случае радиус – это сторона звена DK=a2) на угол поворота этого радиуса (элементарное приращение угла):
![]() (11)
(11)
Аналогично запишем перемещение точки Е:
![]() (12)
(12)
Из соотношений (10-12) следует:
![]() (13)
(13)
Работа силы F2 с учетом (13) получается в виде:
![]() (14)
(14)
Итак, сумма элементарных работ ![]() из соотношений (6), (14) равна
из соотношений (6), (14) равна
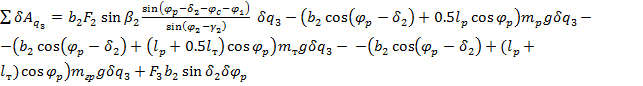 (15)
(15)
Из (15) обобщенная сила на заданном возможном перемещении равна:
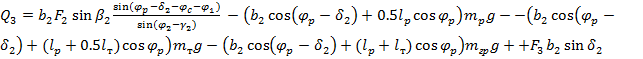 (16)
(16)
При ![]() ,
, ![]() ,
, ![]() ,
, ![]() сумма элементарных работ
сумма элементарных работ ![]() всех активных сил равна
всех активных сил равна
![]()
=![]() (17)
(17)
Из уравнения (17) следует, что обобщенная сила на заданном возможном перемещении равна:
![]() .
.
Ранее авторами была рассчитана кинетическая энергия аналогичной механической системы с тремя степенями свободы [2]. Следовательно, добавив кинетическую энергию телескопической части рукояти манипулятора в виде ![]() получим полную кинетическую энергию системы с четырьмя степенями свободы:
получим полную кинетическую энергию системы с четырьмя степенями свободы:
![]() , где
, где
T1=m1VC12/2 +J1 ω12/2 – кинетическая энергия стрелы,
T2= m2VC22/2 +J2 ω22/2 – кинетическая энергия рукояти,
T3= m3Vгр2/2 – кинетическая энергия груза.
В кинетическую энергию вошли квадраты скоростей центров масс стрелы VC1, рукояти VC2, телескопического удлинителя VC4 и груза Vгр. Для скорости груза получим следующее соотношение (с учетом результатов расчетов в работах [4,5]):
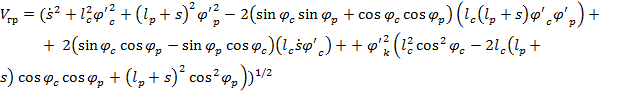 ,где
,где
при ![]() ,
, ![]() ;
;
![]() – скорость движения штока гидроцилиндра привода телескопического удлинителя.
– скорость движения штока гидроцилиндра привода телескопического удлинителя.
Результаты
Подставив все полученные выражения в уравнения (1) составим дифференциальные уравнения Лагранжа II рода:
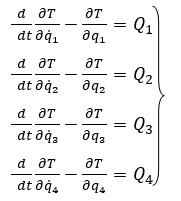
Определена связь между заданным перемещением и перемещениями всех остальных звеньев для каждой степени свободы.
Записана полная кинетическая энергия системы.
Вывод
Выполнен расчет обобщенных сил и кинетической энергии системы, необходимых для записи уравнений Лагранжа II рода.
Цель дальнейшего исследования – решение дифференциальных уравнений для определения зависимости кинематических характеристик от нагрузок.
Рецензенты
Ковалев Рудольф Николаевич, профессор, доктор технических наук, зав. кафедрой экономики и транспорта логистики, Уральский государственный лесотехнический университет, г. Екатеринбург.
Ляпцев Сергей Андреевич, профессор, доктор технических наук, зав. кафедрой технической механики УГГУ, Уральский государственный горный университет, г. Екатеринбург.



