В настоящее время наиболее актуальной задачей при построении систем массового обслуживания в различных областях человеческой деятельности является достижение высокой эффективности функционирования системы при ограниченных ресурсах системы. В данном случае каждая такая система характеризуется следующими особенностями: потоком требований, дисциплиной и функцией распределения длительности обслуживания, очередью. Характеристикой работы данной системы будет являться: оценки вероятностей потерь, длины очереди, ожидания заявки в системе и т.п. Для достижения оптимального функционирования системы в теории массового обслуживания необходим «системный подход», полное и комплексное рассмотрение всех последствий каждого решения.[2] Таким образом, возникает задача нахождения таких параметров системы, при котором достигались бы оптимальные значения основных характеристик работы СМО.
В настоящей работе представлен выбор оптимальной стратегии управления распределением заявок (с точки зрения наименьшего значения предельной очереди в системе) с заданием интенсивностей обслуживания в многоканальной системе массового обслуживания с пуассоновским потоком поступления заявок и экспоненциальным временем обслуживания. Сравниваются три случая распределения заявок на обслуживающие устройства в момент времени t при разных интенсивностях поступления и обслуживания заявок. А именно: равномерное распределение заявок, распределение заявок с наименьшей очередью и распределение заявок на устройство с наименьшим значением произведения интенсивности обслуживания в единицу времени и очереди. Решение задачи представлено методами имитационного стохастического моделирования, включающими формальное построение математической модели, её алгоритмизация, численное нахождение критериев оценки работы СМО.
Математическая модель системы массового обслуживания с роутером и двумя обслуживающими устройствами.
Построим математическую модель для многоканальной СМО с роутером и двумя обслуживающими устройствами в терминах точечных процессов [1]:
Пусть процесс ![]() - точечный считающий процесс числа поступивших в
- точечный считающий процесс числа поступивших в ![]() -ю систему заявок.
-ю систему заявок. ![]() - число заявок в очереди, ожидающих своего обслуживания в момент времени
- число заявок в очереди, ожидающих своего обслуживания в момент времени ![]() .
. ![]() - точечный процесс, описывающий число обслуженных заявок. Тогда основное балансовое уравнение для
- точечный процесс, описывающий число обслуженных заявок. Тогда основное балансовое уравнение для ![]() -ой системы запишется в виде:
-ой системы запишется в виде:
![]() (1)
(1)
где ![]() - число заявок для
- число заявок для ![]() -го сервера в начальный момент времени
-го сервера в начальный момент времени ![]()
![]() ,
, ![]() ,
, ![]() .
.
Схематическая модель многоканальной СМО с роутером выглядит следующим образом:
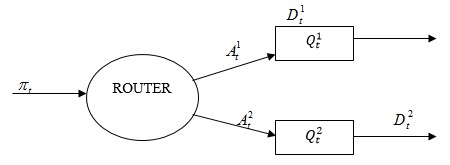
Рис. 1 Общая схема модели СМО
1. Основной поток ![]() - пуассоновский процесс с компенсатором вида:
- пуассоновский процесс с компенсатором вида:
![]() (2)
(2)
где ![]() - интенсивность поступления заявок.
- интенсивность поступления заявок.
2. Процессы ![]() характеризуют работу роутера:
характеризуют работу роутера:
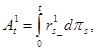 (3.1)
(3.1)
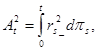 (3.2)
(3.2)
где ![]() ,
,![]() - индикаторные функции, которые могут быть представлены одним из следующих вариантов:
- индикаторные функции, которые могут быть представлены одним из следующих вариантов:
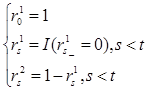 (4.1)
(4.1)
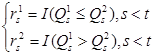 (4.2)
(4.2)
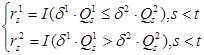 (4.3)
(4.3)
3. ![]() - потоки обслуженных заявок с компенсаторами вида:
- потоки обслуженных заявок с компенсаторами вида:
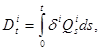 (5)
(5)
где ![]() - интенсивность обслуживания заявок.
- интенсивность обслуживания заявок.
Эксперимент
Пусть ![]() ,
,![]() - интенсивности обслуживания 1-го и 2-го устройств соответственно. Введём,
- интенсивности обслуживания 1-го и 2-го устройств соответственно. Введём,
![]() (6)
(6)
Представим значение ![]() как отношение суммы предельных очередей для 1-го и 2-го устройств для типа распределения (4.1) и (4.2), тогда
как отношение суммы предельных очередей для 1-го и 2-го устройств для типа распределения (4.1) и (4.2), тогда
![]() (7)
(7)
где
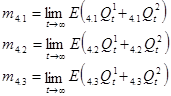 (8)
(8)
Аналогично введём
![]() ,
, ![]() (9)
(9)
Построим при фиксированном значении ![]() графики функций
графики функций ![]() в зависимости от
в зависимости от ![]() .
.
Шаг:
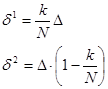 , (10)
, (10)
Где ![]() ,
, ![]() - количество точек.
- количество точек.
Эксперимент 1
|
Параметр |
Значение |
|
Моделируемое время, |
50 000 |
|
|
1,0 |
|
Количество точек, |
10 |
|
Интенсивность поступления заявок, |
0,65 |
|
Предельная очередь, |
1 000 |
|
Предельная очередь, |
1 000 |
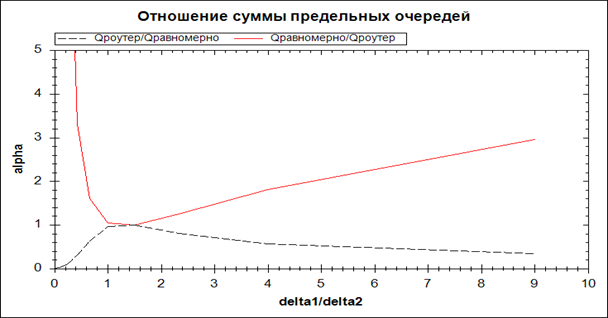
Рис.2. Графики ![]() и
и ![]() в зависимости от
в зависимости от ![]() .
.
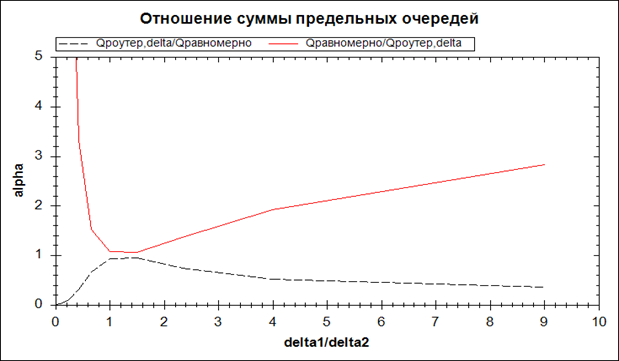
Рис.3. Графики ![]() и
и ![]() в зависимости от
в зависимости от ![]() .
.
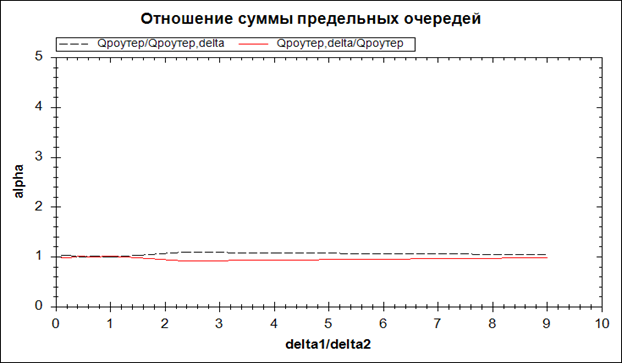
Рис.4. Графики ![]() и
и ![]() в зависимости от
в зависимости от ![]() .
.
Эксперимент 2
|
Параметр |
Значение |
|
Моделируемое время, |
50 000 |
|
|
1,0 |
|
Количество точек, |
10 |
|
Интенсивность поступления заявок, |
1,2 |
|
Предельная очередь, |
1 000 |
|
Предельная очередь, |
1 000 |
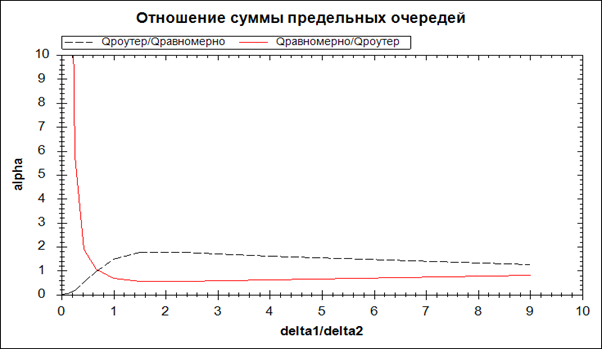
Рис. 5. Графики ![]() и
и ![]() в зависимости от
в зависимости от ![]() .
.
Заключение
1. Модель роутера (4.1) эффективна при отсутствии очереди на приборах (интенсивность прихода заявки в систему ниже общей интенсивности обслуживания)![]() . Причём минимальное значение
. Причём минимальное значение ![]() достигается при
достигается при ![]() .
.
2. Модели роутера (4.2), (4.3) эффективны при ![]() (Интенсивность прихода заявки выше общей интенсивности обслуживания). Причём максимальные значения
(Интенсивность прихода заявки выше общей интенсивности обслуживания). Причём максимальные значения ![]() ,
, ![]() достигаются при
достигаются при ![]() .
.
Рецензенты:
Мищенко С.П., д.ф.-м.н., профессор ФГБОУ ВПО «Ульяновский государственный университет», г. Ульяновск;
Андреев А.С., д.ф.-м.н., профессор ФГБОУ ВПО «Ульяновский государственный университет», г. Ульяновск.



