Задача выявления изменения свойств пуассоновского процесса состоит в следующем. На промежутке действительной оси времени (пространства) наблюдается некоторое количество точек, характеризующее появление однородных событий.
Число точек n и их расположение на выбранной оси является случайным (координаты ![]() ).
).
Последовательность независимых одинаково распределённых случайных величин ![]()
![]()
![]()
![]() для пуассоновского потока имеет функцию распределения
для пуассоновского потока имеет функцию распределения ![]() .[1]
.[1]
Пусть ![]() имеют функции распределения
имеют функции распределения ![]() . Требуется определить момент «разладки» пуассоновского потока
. Требуется определить момент «разладки» пуассоновского потока ![]() .
.
После наблюдения на интервале ![]() моментов появления случайного события (
моментов появления случайного события (![]() ) будем решать задачу о различении следующих двух гипотез
) будем решать задачу о различении следующих двух гипотез ![]() : «разладки» нет,
: «разладки» нет, ![]() : «разладка» есть [5].
: «разладка» есть [5].
Зафиксируем уровень значимости ![]() и определим тест для различения этих гипотез неравенством
и определим тест для различения этих гипотез неравенством
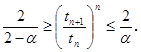 (1)
(1)
Выбор теста (1) можно объяснить следующим образом. Введем в рассмотрение тестовую статистику ![]() (разность статистических оценок энтропии).
(разность статистических оценок энтропии).
![]()
где ![]()
![]() - оценка дифференциальной энтропии, определенная по
- оценка дифференциальной энтропии, определенная по ![]() (соответственно по
(соответственно по ![]() ) наблюдениям случайной последовательности
) наблюдениям случайной последовательности ![]() с экспоненциальным распределением времени между двумя смежными событиями. Можно показать, что тестовая статистика имеет вид
с экспоненциальным распределением времени между двумя смежными событиями. Можно показать, что тестовая статистика имеет вид
![]()
где ![]() – случайная величина, определяемая следующим соотношением
– случайная величина, определяемая следующим соотношением ![]() [6].
[6].
Действительно, так как эмпирическое значение дифференциальной энтропии для выборок из экспоненциальных генеральных совокупностей имеет вид
![]()
где ![]() – оценка математического ожидания промежутков времени между двумя смежными событиями, то
– оценка математического ожидания промежутков времени между двумя смежными событиями, то
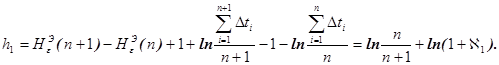
Функция распределения случайной величины ![]() , является инвариантной к параметру
, является инвариантной к параметру ![]() экспоненциального распределения
экспоненциального распределения ![]() и имеет плотность [6;7]
и имеет плотность [6;7]
![]()
Для доказательства этого утверждения прежде всего заметим, что если случайная величина ![]() представляет собой сумму экспоненциально распределённых случайных величин
представляет собой сумму экспоненциально распределённых случайных величин ![]() , то она в свою очередь будет распределена по закону гамма-распределения с параметром формы
, то она в свою очередь будет распределена по закону гамма-распределения с параметром формы ![]() [2]. Отсюда следует, что плотность отношения двух независимых случайных величин
[2]. Отсюда следует, что плотность отношения двух независимых случайных величин ![]() и
и ![]() определяется следующим образом
определяется следующим образом
![]() (2)
(2)
Учитывая, что
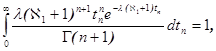
после очевидного преобразования интеграла (2) находим
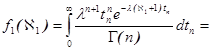
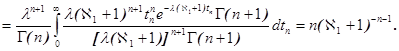
Используя плотность распределения ![]() , можно определить плотность распределения статистики
, можно определить плотность распределения статистики ![]() [7]
[7]
![]()
Для этого достаточно преобразовать плотность распределения с учётом соотношения между случайными величинами ![]() и
и ![]()
![]() .
.
Функция распределения тестовой статистики ![]() непосредственно определяется из её плотности [3]
непосредственно определяется из её плотности [3]
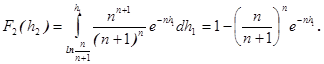
Заметим, что область задания статистики критерия ограничена снизу значением ![]() . Доверительные границы для теста проверки «разладки» пуассоновского процесса, соответствующие доверительному уровню
. Доверительные границы для теста проверки «разладки» пуассоновского процесса, соответствующие доверительному уровню ![]() , могут быть определены с помощью функции распределения
, могут быть определены с помощью функции распределения ![]() следующим образом:
следующим образом:
![]()
Несложные преобразования этого неравенства дают удобную формулу (1) для теста (решающее правило).
Введённый в рассмотрение тест (1) представляется целесообразным дополнить ещё одним тестом, повышающим эффективность процедуры выявления момента «разладки».
Из рассмотрения теста (1) вытекает, что он становится малоэффективным («некритичным»), если пуассоновский поток имеет тенденцию к вырождению в регулярный поток. Указанный недостаток можно устранить, если ввести в рассмотрение тестовую статистику ![]() [3].
[3].
![]()
где ![]() – оценка дифференциальной энтропии, определённая по
– оценка дифференциальной энтропии, определённая по ![]() (соответственно по
(соответственно по ![]() ) стандартным нормализованным случайным величинам
) стандартным нормализованным случайным величинам ![]() , определяемым по зависимости
, определяемым по зависимости
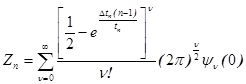
по наблюдениям последовательности ![]() .
.
Как и в предыдущем случае можно показать, что
![]() ,
,
а плотность распределения случайной величины 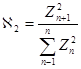 имеет вид:
имеет вид:
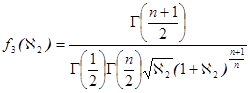 . (3)
. (3)
Соответственно и статистика ![]() будет иметь плотность распределения вида
будет иметь плотность распределения вида
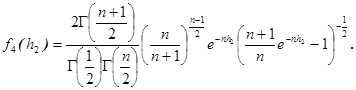 (4)
(4)
Доверительные границы для второго теста, соответствующие уровню ![]() , могут быть определены на основе полученных выражений для плотностей распределения тестовых статистик
, могут быть определены на основе полученных выражений для плотностей распределения тестовых статистик ![]() (или
(или ![]() ) [7; 9].
) [7; 9].
Однако получить решающее правило в удобной форме, как это удалось получить для первого теста, в данном случае не представляется возможным. С вычислительной точки зрения процедура проверки гипотезы с использованием плотностей распределений (3) или (4) принципиальных трудностей не вызывает.
Действительно, в силу того, что интегральная функция распределения ![]() не может быть получена в аналитическом виде, границы критической области определяются численными методами приближённых вычислений из уравнений
не может быть получена в аналитическом виде, границы критической области определяются численными методами приближённых вычислений из уравнений
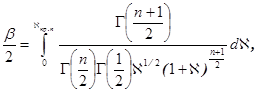 (5)
(5)
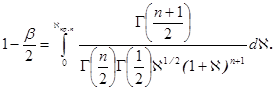 (6)
(6)
Следовательно, окончательно решающее соотношение запишется в виде следующего неравенства
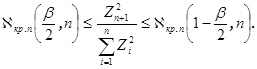
По зависимостям (5) и (6) определяются правая ![]() и левая
и левая ![]() границы критической области теста 2.
границы критической области теста 2.
Результаты вычислений для различных уровней значимости ![]() представлены в табл. 1, из которой нетрудно заметить, что с увеличением объёма последовательности
представлены в табл. 1, из которой нетрудно заметить, что с увеличением объёма последовательности ![]() и уровня значимости
и уровня значимости ![]() область доверия сужается [3;8;10].
область доверия сужается [3;8;10].
Таблица 1
Границы критической области для теста 2
|
n+1 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
2 |
0,0273 |
51,49 |
0,0625 |
20,57 |
0,1153 |
10,79 |
|
3 |
0,0108 |
5,39 |
0,0251 |
3,07 |
0,0446 |
2,03 |
|
4 |
0,0068 |
2,36 |
0,0153 |
1,47 |
0,0278 |
1,03 |
|
5 |
0,0048 |
1,47 |
0,0109 |
0,95 |
0,0197 |
0,69 |
|
6 |
0,0038 |
1,07 |
0,0085 |
0,71 |
0,0155 |
0,52 |
|
7 |
0,0031 |
0,85 |
0,007 |
0,56 |
0,0128 |
0,42 |
|
8 |
0,0026 |
0,7 |
0,0058 |
0,47 |
0,0106 |
0,35 |
|
9 |
0,0023 |
0,6 |
0,0051 |
0,41 |
0,0092 |
0,3 |
|
10 |
0,002 |
0,53 |
0,0045 |
0,36 |
0,0082 |
0,26 |
|
11 |
0,0018 |
0,47 |
0,004 |
0,32 |
0,0073 |
0,24 |
|
12 |
0,0016 |
0,43 |
0,0037 |
0,29 |
0,0067 |
0,21 |
|
13 |
0,0015 |
0,39 |
0,0034 |
0,27 |
0,0059 |
0,18 |
|
14 |
0,0013 |
0,57 |
0,0031 |
0,24 |
0,0055 |
0,17 |
|
15 |
0,0012 |
0,34 |
0,0028 |
0,23 |
0,0051 |
0,16 |
|
16 |
0,0011 |
0,32 |
0,0026 |
0,21 |
0,0048 |
0,15 |
Заметим также, что введённый в рассмотрение второй тест в силу его чувствительности к дисперсии нормализованной случайной величины является критичным к тенденции вырождения пуассоновского потока в регулярный.
Таким образом, введённые в рассмотрение тесты выявления пуассоновского потока позволяют выявить момент изменения свойств случайной последовательности событий и перейти от пуассоновской модели редких событий к одной из её модификаций.
Одной из таких модификаций, описывающей статистическую структуру, возникающую из комбинации простейших пуассоновских потоков, является распределение Пуассона степени ![]() , производящая функция которого имеет вид: [7;8]
, производящая функция которого имеет вид: [7;8]
![]() .
.
Это распределение можно охарактеризовать следующими параметрами:
математическим ожиданием [4;5]
![]()
дисперсией (вторым центральным моментом)
![]()
Из полученных соотношений следует, что отношение дисперсии к математическому ожиданию для этого распределения зависит только от параметра ![]() .
.
Следовательно, при помощи этой зависимости можно определить параметр kпо выборочным значениям моментов [5]
Обобщённое распределение Пуассона порядка ![]() формируется следующим образом.
формируется следующим образом.
Пусть ![]() – производящая функция вероятностного распределения, сосредоточенного на множестве целых чисел
– производящая функция вероятностного распределения, сосредоточенного на множестве целых чисел ![]() , а
, а ![]() – производящая функция распределения Пуассона.
– производящая функция распределения Пуассона.
Тогда производящая функция ![]() обобщённого пуассоновского распределения порядка
обобщённого пуассоновского распределения порядка ![]() определяется формулой [7]
определяется формулой [7]
![]()
Так, например, если ![]() – производящая функция биномиального распределения
– производящая функция биномиального распределения
![]() ,
,
то
![]()
![]()
![]() и т.д.
и т.д.
Однопараметрическое распределение ![]() может рассматриваться как составное пуассоновского (усечённое в конце) распределения, параметры которого подчиняются показательному распределению со средним значением, равным
может рассматриваться как составное пуассоновского (усечённое в конце) распределения, параметры которого подчиняются показательному распределению со средним значением, равным ![]() .
.
Рецензенты:
Хасцаев Б.Д., д.т.н., профессор, декан факультета электронной техники, Северо-Кавказский Ордена Дружбы Народов горно-металлургический институт (Государственный технологический университет), г. Владикавказ.
Шелехов П.Ю., д.т.н., профессор кафедры «Детали машин», Северо-Кавказский Ордена Дружбы Народов горно-металлургический институт (Государственный технологический университет), г. Владикавказ.



