Наводнения являются регулярным циклическим стихийным бедствием, ежегодно приносящим значительный ущерб экономики различных регионов, а в некоторых экстремальных случаях и уносящих человеческие жизни. Разработка систем мониторинга водных бассейнов, эффективное прогнозирование состояние водных бассейнов является важной задачей минимизации ущерба от паводковых наводнений.
При разработке противопаводковых систем [1-3] возникает задача адекватной оценки площади затопления местности для последующей оценки возникающих угроз и масштаба материального ущерба в результате затопления инфраструктуры, объектов хозяйственной деятельности, жилых районов.
Данная задача является особо актуальной в случае предварительного прогнозирования ситуации в системах противопаводкого мониторинга, когда в качестве исходных данных имеется лишь прогнозируемый уровень воды в контрольной точке измерения и нет возможности проведения аэрофотосъемки и фактической фиксации масштаба ущерба на местности.
Уровень воды водоема позволяет специалисту по чрезвычайным ситуациям оценить лишь косвенно возникающую опасность. Нахождение изменяющегося контура береговой линии водоема своевременно обнаружить объекты, попадающие в зону возможного затопления и произвести необходимые мероприятия по минимизации ущерба, причиняемого наводнением.
Многие современные методы определения площади затопления основываются на вероятностных методах анализа статистических данных долговременных наблюдений. Данные методы не позволяют с необходимой точностью определить точный контур измененной береговой линии и уровень воды в различных точках затопления.
Для решения поставленной задачи предлагается производить точную трех мерную реконструкцию поверхности анализируемой местности и производить необходимые замеры используя построенную модель и данные объективного контроля уровня воды или его прогнозируемые значения.
Обобщенный алгоритм решения задачи нахождения контура береговой линии, площади и объема затопления представлен на рисунке 1.
В качестве исходных данных для реконструкции поверхности используется уровень поверхности воды в водоеме относительно уровня моря, географические координаты точки наблюдения (широта и долгота), ширина и протяженность анализируемой площади, уровень детализации (определяет точность и скорость построения модели).
На первом этапе производится нахождение географических координат граничных точек анализируемой местности. После чего вся площадь разбивается на сетку, представляющую собой массив промежуточных точек интервал между которыми зависит от заданного уровня детализации модели.
Далее стоит задача получения для каждой географической точки ее высоты относительно уровня моря. Для этого могут быть использованы различные открытые геоинформационные сервисы, такие как googlemap, яндекс карты и др. Данные сервисы на данный момент имеют точность по высоте координат до 1 метра, что является достаточно грубым измерением, однако качество данных геоинформационных систем постоянно растет, а также в случае наблюдения конкретного участка местности может быть произведена его специальная аэрофотосъемка, а также данные могут быть получены из любой другой базы данных топографических измерений. Так как рельеф местности со временем меняется незначительно, то данная операция должна быть произведена единожды, что позволит точно определять прогнозируемые масштабы затопления.
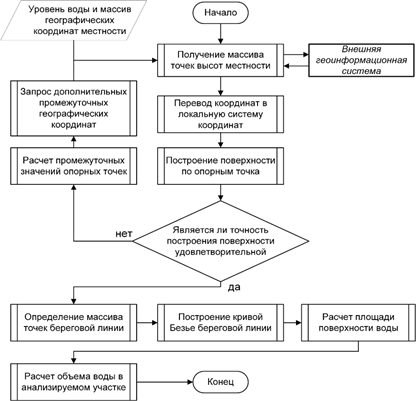
Рисунок 1 – Алгоритм расчета площади и объема затопления
После получения высот для всех географических координат точек исследуемого участка водоема следует перевести их в локальную систему координат. Для этого следует выбрать одну точку в качестве начала отчета, координаты всех остальных точек находятся относительно нее по следующим зависимостям.
![]() ; (1)
; (1)
![]() ; (2)
; (2)
![]() , (3)
, (3)
где ![]() – координаты i-ой точки в локальной системе координат;
– координаты i-ой точки в локальной системе координат; ![]() – долгота i-ой точки и точки, принятой в качестве начала координат в локальной системе координат соответственно;
– долгота i-ой точки и точки, принятой в качестве начала координат в локальной системе координат соответственно; ![]() – широта и высота i-ой точки и точки, принятой в качестве начала координат в локальной системе координат соответственно; R – радиус Земли.
– широта и высота i-ой точки и точки, принятой в качестве начала координат в локальной системе координат соответственно; R – радиус Земли.
Переведя координаты всех точек в локальную систему координат, можно строить поверхность рельефа местности. Для построения поверхности по массиву точек лучше всего подходят поверхности Безье [4]. Применяя формулу (4), можно составить уравнение поверхности Безье:
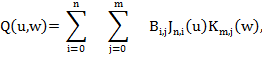 (4)
(4)
где ![]() и
и ![]() есть базисные функции Бернштейна в параметрических направлениях u и w, представленные на формулах (5) и (6). Если при проецировании поверхности местности на плоскость с наложенной полигональной сеткой, вершинами сетки являются полученные ранее точки
есть базисные функции Бернштейна в параметрических направлениях u и w, представленные на формулах (5) и (6). Если при проецировании поверхности местности на плоскость с наложенной полигональной сеткой, вершинами сетки являются полученные ранее точки ![]() , то u и w – являются параметрами, определяющими координаты по горизонтали и вертикали соответственно в пространстве локальной системы координат. Параметры u, w изменяются от 0 до 1, при этом точка с координатами [0,0] является начальной точкой построения, а точка с координатами [1,1] – конечная точка построения (рис. 2).
, то u и w – являются параметрами, определяющими координаты по горизонтали и вертикали соответственно в пространстве локальной системы координат. Параметры u, w изменяются от 0 до 1, при этом точка с координатами [0,0] является начальной точкой построения, а точка с координатами [1,1] – конечная точка построения (рис. 2).
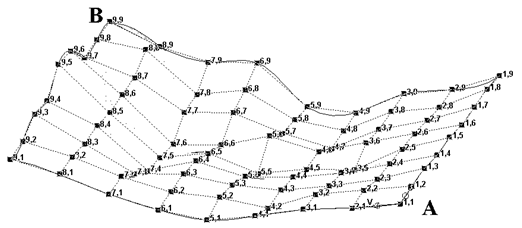
Рисунок 2 – Полигональная сетка рельефа анализируемой местности (А – начальная точка построения, В – конечная точка построения)
![]() ; (5)
; (5)
![]() ; (6)
; (6)
![]() ; (7)
; (7)
![]() , (8)
, (8)
где n, m – количество вершин полигональной сетки по горизонтали и вертикали соответственно; i, j – индексы конкретной вершины по горизонтали и вертикали.
После построения поверхности, проверяется ее точность. Для этого находится расстояние между произвольными точками ![]() и
и ![]() , которое определяется как расстояние между точками S по теореме Пифагора
, которое определяется как расстояние между точками S по теореме Пифагора
![]() . (9)
. (9)
Если найденное расстояние S больше константы, принятой в качестве максимального расстояния между точками, то следует провести разбиение опорных точек поверхности. Для поверхности Безье можно провести разбиение методом рекурсивного разбиения Безье.
Поверхность Безье состоит из набора линий Безье. Для разбиения точек поверхности на дополнительные точки следует поочередно разбивать каждую составляющую ее кривую. Разбиение может производиться до тех пор, пока не будет достигнута требуемая точность.
После того, как разрешающая способность поверхности удовлетворяет заданной точности, следует определить точки, составляющие границу разлива (рис. 3).

Рисунок 3 – Пересечение восстановленной поверхности местности с плоскостью уровня водоема образующая береговую линию разлива.
Для этого производится последовательный обход полигональной сетке, при этом для линий, образованных каждой последовательной парой точек проверяется условие пересечения с уровнем воды. Пересечение имеется в случае если высота уровня воды находится в диапазоне высот рассматриваемых точек. В случае если обнаружено пересечение, то определяется у какой из точек координата высоты ближе к уровню поверхности воды. Для этого находится расстояние до каждой из точек. Точка наиболее близкая к уровню воды, сохраняется в массиве точек, содержащих границу разлива, если у обеих точек разность равна, сохраняются обе точки.
При записи в массив точек, содержащих границу разлива координаты новой точки в локальной системе координат, также сохраняются координаты этой точки в параметрической системе координат UoW, эти параметры используются при расчете объема воды.
На рисунке 4 представлена проекция полигональной сетки поверхности поймы реки на плоскость XoY, которая также изображена на рисунке 2. На рисунке видно, что для точки А необходимо проверять пересечение с поверхностью воды на отрезках АВ и АС, так как при проходе по полигональной сетке точки В и С являются следующими за точкой А по горизонтали и вертикали соответственно. Так в массиве точек, составляющих контур затопления будет сохранена точка А, учитывающая разность между ее координатой z и соответствующей координатой поверхности воды, которая оказалась по модулю меньше соответствующей разности для точек С и В.
Затем по получившимся точкам строиться кривая Безье [6], которая и будет являться контуром разлива. Построение кривой Безье практически аналогично построению поверхности Безье, для этого были использованы Следующая зависимость:
![]() (10)
(10)
Для получения площади разлива воды применялся метод средних прямоугольников численного интегрирования [5], представленного в виде зависимостей:
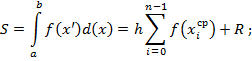 ((11)
((11)
![]() ((12)
((12)
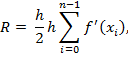 ((13)
((13)
где R – погрешность вычисления; n – число разбиений интервала интегрирования; i – индекс конкретной вершины; h – значение шага в локальной системе координат.
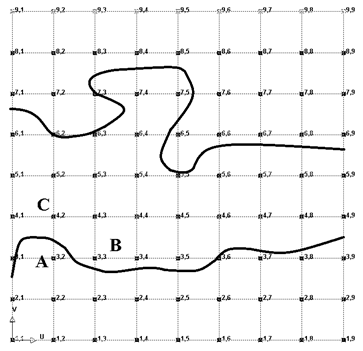
Рисунок 4 – Полигональная сетка рельефа местности с отмеченным контуром пересечения с водой
Площадь может быть вычислена итерационно перебирая точки в направлении u с заданным константным шагом. Вычисления производятся до тех пока u не станет равной 1. На каждой итерации выбирается одно значение координаты x и соответствующие ей два значения y, полученных на противоположных береговых линиях. После чего находится площадь сегмента в соответствии сформулой (11), где ![]() – является расстоянием между значениями координат y. Сумма площадей всех сегментов является общей площадью разлива водоема (11).
– является расстоянием между значениями координат y. Сумма площадей всех сегментов является общей площадью разлива водоема (11).
Для расчета объема воды применялся метод средних прямоугольников для трехмерной системы координат.
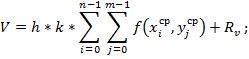 (14)
(14)
![]() (15)
(15)
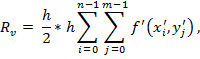 (16)
(16)
где ![]() – разность между координатой z поверхности воды и соответствующей координатой обрабатываемой точки; k – значение шага в локальной системе координат для направления oY; h – шаг для направления oX.
– разность между координатой z поверхности воды и соответствующей координатой обрабатываемой точки; k – значение шага в локальной системе координат для направления oY; h – шаг для направления oX.
Для нахождения объема воды перебираются точки на полигональной сетке поверхности рельефа местности с заданным шагом для направлений u и w, данные параметры изменяются в пределах значений, которые были сохранены для каждой точки контура разлива. В процессе перебора точек вычисляется объем воды.
На заключительном этапе найденные точки контура разлива переводятся из локальной системы координат в географические координаты, которые могут быть использованы в геоинформационных системах и системах мониторинга бассейнов водоемов.
Полученные в результате расчетов береговые линии могут быть нанесены на интерактивные карты, что позволит наглядно отслеживать результат прогнозируемой ситуации в системах мониторинга бассейнов водоемов.
Предложенный в статье метод определения площади разлива водоемов позволяет определить какие участки местности будут затоплены при достижении уровня воды заданной отметки. В случае если в системе противопаводкового мониторинга имеется информация об населенных пунктах, располагающихся на берегу рек и других объектов хозяйственной деятельности, то предложенный метод позволит определить множество объектов, подлежащих затоплению. При чем, для каждого из них имеется возможность определить уровень воды преходящей в результате затопления. Как следствие на основании данной информации появляется возможность оценки возможного ущерба, вызванного наводнением.
При наличии полной карты высот всего бассейна рек и информации о геологическом составе почв на основании приведенных методов расчета объема вод, можно более точно предсказывать развитие ситуации за счет создания динамических моделей перемещения вод по рельефу местности.
На базе построенной трехмерной модели местности также появляется возможность более точного предсказания повышения уровня воды в начале весенних паводков, так как создание динамической модели позволить произвести оценку объема стока талой воды и соответственно сезонное повышение уровня воды в бассейнах открытых водоемов.
Статья подготовлена в рамках гранта РФФИ «Исследование и разработка метода и автоматической системы противопаводкового мониторинга уровня воды открытых водоемов» (проект № 13-01-90351).
Рецензенты:
Шведенко В.Н., д.т.н., профессор, зав. кафедрой «Информационные технологии» Костромского государственного технологического университета, г. Кострома;
Коськин А.В., д.т.н., профессор, проректор по информатизации ФГБОУ «Государственный университет учебно-научно-производственный комплекс», г. Орел.



