В [1] развита вероятностно-статистическая модель учащегося, в соответствии с которой каждый индивидуум в процессе обучения идентифицируется функцией распределения (плотностью вероятности), распространяющейся в информационном пространстве. На основе закона сохранения вероятности записана система дифференциальных уравнений, представляющих собой уравнения непрерывности, которые связывают изменения плотности вероятности за единицу времени в фазовом пространстве (пространстве координат и кинематических величин различных порядков) с дивергенцией плотности потока вероятности в рассматриваемом фазовом пространстве. В случае, когда средняя скорость движения плотности вероятности не зависит от координаты, уравнение непрерывности принимает вид
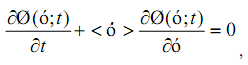
где Ø(ó;t) - плотность вероятности; ó - координата в информационном пространстве; < ó > - средняя скорость; t - время.
Из [1] непосредственно следует, что его решением должна быть функция аргумента (< ó > t - ó), т. е.
Ø(ó; t) = Ø(< ó > t - ó) (2)
Уравнение (2) является уравнением волны, распространяющейся в информационном пространстве. Следовательно, (2) должно быть также и решением соответствующего волнового уравнения. Найдём это уравнение. С этой целью продифференцируем (1) два раза независимо по времени и координате и, принимая во внимание, что
∂ Ø(ó;t)/∂t∂ ó = ∂ Ø(ó;t)/∂ ó∂t
после несложных преобразований получим волновое уравнение для плотности вероятности:
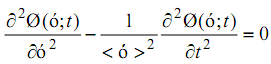 . (3)
. (3)
Подставляя (2) в (3),можно убедиться, что уравнение волны (2) является решением волнового уравнения (3).
СПИСОК ЛИТЕРАТУРЫ
1. Романов В.П., Соколова Н.А. Вероятностно-статистическая модель учащегося // Современные проблемы науки и образования. - 2009, № 6 (Часть 3.). - С. 122-129.



