Разработка газовых и нефтяных месторождений в шельфе неминуемо многократно увеличивает риски возникновения аварийных ситуаций и как следствие загрязнение Мирового океана нефтепродуктами. При этом очень важную роль играет как способ устранения аварий такого рода, так и изучение миграции углеводородов, изменение их теплофизических характеристик. Актуальность изучения данной тематики тесно связана с проблемой охраны прибрежной и шельфовой зоны морей и океанов от загрязнений [4], вызванных утечкой нефти и газа. Большой вклад в изучение затопленных струй внес Г.Н. Абрамович в работе [1], в которой описаны автомодельные асимптотические решения [1].
Постановка задачи. Пусть на дне водоема существует источник истечения углеводородов (нефть и газ) с известной температурой и объемным расходом. Считаем, что известны теплофизические характеристики окружающей воды и углеводородов. Необходимо получить зависимость каждого параметра многофазной струи от вертикальной координаты. Считаем, что миграция углеводородов происходит в рамках затопленной струи.
Для получения модели, описывающей течении углеводородов, примем ряд допущений. Считаем, что капли нефти, пузырьки газа и вода, вовлекаемая в струю, имеют одинаковые температуру, скорость и траекторию в каждом сечении струи. Капли нефти не слипаются, не деформируются. Ось z направлена вертикально вверх. В теоретической части особенное внимание в исследовании струи уделено процессу охлаждения струи из-за «захвата» окружающей воды.
§1 Приближенная модель
Методика расчета предложена в [5]. Результаты, которые получены на основе этой модели, носят приближенный характер.
Зная начальный радиус скважины, из которой происходит истечение углеводородов, получим начальную площадь поперечного сечения струи: 
.
Скорость течения смеси определим как 
, 
, здесь 
, 
– начальные объемные расходы нефти и газа.
Удельный поток импульса на устье скважины выразится через скорость течения и объемный расход смеси: 
.
Сила плавучести на единицу массы представляется в виде: 
,
где 
– плотность окружающей воды, 
– плотность истекающей смеси, g– ускорение свободного падения.
Удельный поток плавучести: 
.
Расстояние, на котором удельный импульс силы плавучести превышает удельный импульс, приобретаемый струей вначале: 
.
Время для перемещения объема жидкости на расстояние z: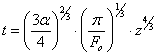 
.
Радиус струи на высоте z представляется в виде: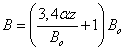 
.
Скорость подъема струи в сечении z: 
.
Объемный расход представим в следующем виде: 
.
Таким образом, можно определить температуру в любом сечении струи, считая, что температура в сечении струи одинаковая и зависит только от координаты z:
,
где Tw, T0 – температуры окружающей воды и вытекающей жидкости, Q0 – начальный объемный расход.
§2 Численная модель расчета параметров струи
Идея модели основана на методе конечных объемов и описана в [5]. Считается, что струя состоит из последовательности элементов, каждый из которых обладает набором следующих характеристик − радиус, высота, скорость, масса и координаты.
На k шаге элемент струи располагается в точке 
со следующими компонентами скорости
, при этом скорость определяется как 
здесь 
− горизонтальные составляющие скорости, 
вертикальная составляющая скорости. Для простоты полагаем, что горизонтальные составляющие скорости струи нулевые.
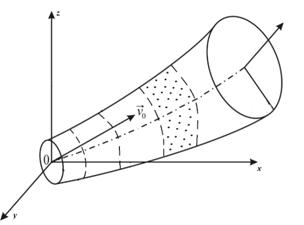
Рис.1 Схема метода конечных объемов
Для моделирования струи разобьем её на элементы – контрольные объемы, обладающие координатами и значениями радиуса струи – bk, высота элемента в данный момент времени − hk.
Тогда масса контрольного объема определится следующим образом:
.
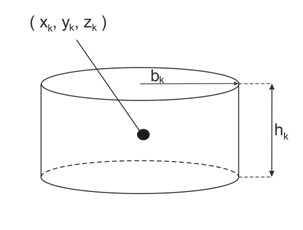
Рис. 2 Схема контрольного объема
Дополнительно используют следующие характеристики среды: температура Tk и плотность
.
Законы сохранения масс для воды, газа, нефти и гидрата в контрольном объеме (КО):
, 
, 
, 
,
где 
, 
, 
, 
, 
– объемное содержание i- й фазы, 
– плотность i- й фазы.
Закон сохранения числа частиц в контрольном объеме :
.
Масса всего контрольного объема (КО):
.
Закон сохранения импульсов:
,
,
.
Закон сохранения энергии для контрольного объема (КО):
.
,
Толщина и радиус контрольного объема на следующем шаге:
, 
.
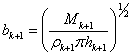Направление струи: 
, 
,
, 
.
Координата контрольного объема на следующем шаге:
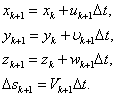
Начальные и граничные условия:
, 
, 
, 
.
,
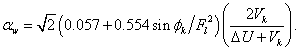
Выводы
В работе представлены две модели затопленных струй. Приведена методика расчета теплофизических и кинематических параметров. Вследствие «захвата» окружающей воды струей происходит охлаждение струи до температуры окружающей среды.
Рецензенты:
Гималтдинов И.К., д.ф.-м.н., профессор, заведующий кафедрой «прикладная информатика и программирование» Стерлитамакского филиала ФГБОУ ВПО «Башкирский государственный университет», г. Стерлитамак.
Мустафина С.А., д.ф.-м.н., профессор, заведующая кафедрой «математическое моделирование», декан физико-математического факультета Стерлитамакского филиала ФГБОУ ВПО «Башкирский государственный университет», г. Стерлитамак.