Эффективным способом борьбы с многолучевостью является разнесенный прием по времени прихода лучей с последующим их сложением по методу квадратичного суммирования [1, 6]. При этом в каналах с дискретной многолучевостью с задержками лучей 2–3 мс возможно использование сложных сигналов с небольшой базой. Однако данный способ не находит практического применения, так как характеристики известных ансамблей Уолша, Велти, Радемахера не отвечают требованиям «узости» огибающих авто- и взаимокорреляционных функций, а существующие методы синтеза ансамблей дискретных ортогональных в усиленном смысле сигналов реализуют лишь требование ортогональности в усиленном смысле и не учитывают требования к корреляционным характеристикам сигналов. Рассмотрим линейные унитарные преобразования с целью разработки нового метода синтеза ансамблей сигналов, удовлетворяющих заданным требованиям.
Целью исследований является анализ зависимости корреляционных характеристик сигналов ансамбля от параметров унитарного оператора. Полученные результаты позволят синтезировать системы дискретных ортогональных сигналов с требуемыми корреляционными свойствами.
Материал и метод исследования. В общем случае любой ансамбль сигналов можно представить в виде набора функций:
где хk(t)ÎL2(0;Т), для k=1,2,…,n.
В качестве сигналов целесообразно рассматривать лишь те функции, энергия которых на конечном интервале конечна, т.е.:
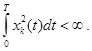
В случае линейного варианта разделения сигналов необходимо, чтобы функции, описывающие их, были линейно независимыми.
Функция, задающая дискретный сигнал, является кусочно-постоянной, т.е. если х(t) задает дискретный сигнал на отрезке времени [0;T], то:
где Аi – некоторое число в общем случае комплексное, {ti} – конечное покрытие отрезка [0;T], т.е.:
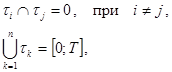
где n – число значений, которое принимает сигнал.
Комплексную огибающую любого дискретного сигнала можно представить в виде совокупности конечного числа прямоугольных импульсов с длительностью t, амплитудами аi и фазами ji[2]. Таким образом, комплексная огибающая х(t) однозначно определяется вектором в n-мерном комплексном пространстве:
где 
.
Пусть сигналы ансамбля задаются столбцами матрицы вида:
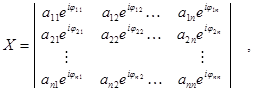(1)
где n- размерность ансамбля, т.е. количество различных сигналов в ансамбле.
Ограничимся рассмотрением ансамблей сигналов с пик-фактором огибающей равной 1 т.е. arq=a=const.
При некогерентном приеме сигналов важны значения огибающей корреляционных функций [5]. Соотношение, описывающее огибающие, имеет вид [7]:
(3)
где m – номер бокового пика корреляционной функции, * – знак комплексного сопряжения.
В формулах (2) и (3) при r = q описываются боковые пики огибающей автокорреляционной, а при r ¹ q – взаимокорреляционной функции.
Распишем соотношение (3), например, для первого и второго бокового пика. Для этого подставим (1) в соотношение (3)при m=1и m=2:
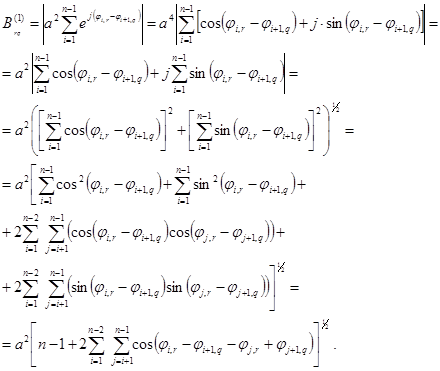(5)
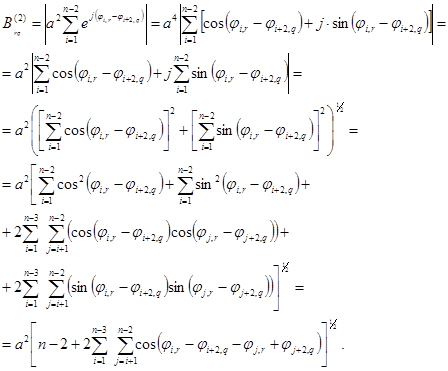(6)
Тогда (3) можно записать в виде:
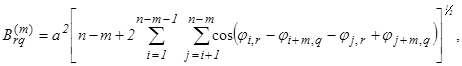(8)
где m изменяется от 0 до n-2.
Распишем соотношение (8):
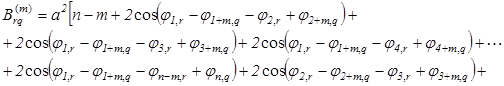
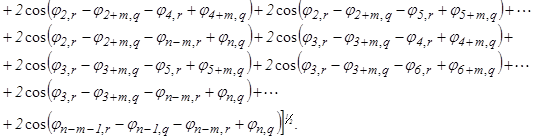(9)
Очевидно, что подкосинусные выражения слагаемых, начиная с n-m-2-го, являются линейной комбинацией подкосинусных выражений первых n-m-1 слагаемых:
и т.д.
Теперь соотношение (8) можно записать:
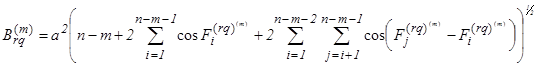(10)
где 
определяется соотношением:
(11)
Таким образом, величины 
однозначно определяют значения боковых пиков автокорреляционных при r = q и взаимокорреляционных при r ¹ q функций сигналов ансамбля.
Рассмотрим преобразование вида:
где А – унитарный оператор, т.е.:
* – знак эрмитова сопряжения, I – единичная матрица.
Унитарные операторы сохраняют скалярное произведение векторов, а также сложение векторов и произведение векторов на скаляр. Таким образом, при унитарных преобразованиях норма векторов, расстояния, углы, ортогональность и ортонормированность инвариантны [3,4].
Пусть матрица, задающая унитарный оператор А, имеет вид:
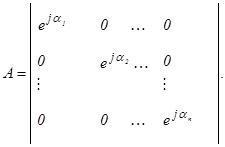(12)
Очевидно, что унитарное преобразование вида (12) не изменяет пик-фактор огибающей сигналов. Матрица 
новых сигналов имеет вид:
(13)
Очевидно, что соотношения для боковых пиков огибающих корреляционных функций для новых сигналов будут включать параметры унитарного оператора в виде фазовых коэффициентов αi. Распишем соотношение для первого и второго бокового пикановых сигналов:
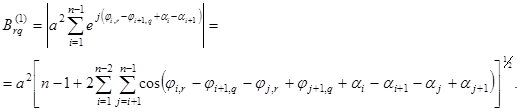
(15)
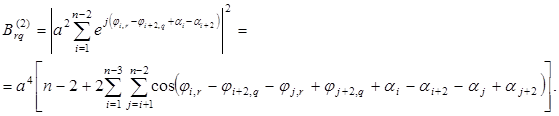(16)
Таким образом, соотношение (10) можно переписать:
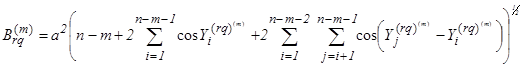(18)
где
(19)
Рассмотрим соотношение (19) для m-го бокового пика корреляционной функции. Таких соотношений будет n-m-1:
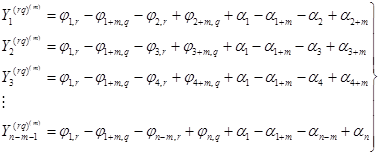. (20)
Перепишем систему (20) в матричном виде:
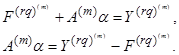(21)
Система (21) имеет n-m-1 уравнения и n неизвестных, следовательно, существует бесчисленное множество решений. В этом случае необходимо m-1 свободную переменную перенести в правую часть системы (21) и для простоты приравнять их к нулю, тогда система будет иметь единственное решение.
Результаты исследований. Таким образом, анализируя соотношения (18), (19), можно сделать вывод, что величины 
однозначно определяют значения боковых пиков автокорреляционных при r = q и взаимокорреляционных при r ¹ q функций сигналов ансамбля.
Обозначим через {Y(m)} множество допустимых значений, при которых уровень m-гобокового пика корреляционной функции лежит в заданных пределах. Очевидно, что для всех m-х боковых пиков корреляционных функций это множество будет одним и тем же. Множество {Y(m)} представляет собой прямоугольную матрицу с n-m-1 строками.
Тогда систему уравнений (21) можно записать:
(22)
где{a} – область допустимых решений для m-го бокового пика квадрата огибающей корреляционной функции r и q сигналов, представляющая собой прямоугольную матрицу, в столбцах которой содержатся наборы разрешенных значений переменных an, А(m) – матрица коэффициентов переменных an.
Выводы. Таким образом, задача синтеза сводится к отысканию совместной области допустимых решений для всех 
и для всех 
.
Рецензенты:
Калмыков И.А., д.т.н., профессор, профессор кафедры информационной безопасности автоматизированных систем Северо-Кавказского федерального университета, г. Ставрополь.
Шуваев А.В., д.э.н., профессор, профессор кафедры информационных систем Ставропольского государственного аграрного университета, г. Ставрополь.