В данной работе представлены результаты первого этапа исследований по созданию полной математической модели процессов термо-газодинамики и тепло-массообмена на поверхности гиперзвукового летательного аппарата (ГЛА) при полёте в атмосфере на высотах, удовлетворяющих по параметрам модели сплошной среды.
Актуальность работы обусловлена тем, что одной из важнейших проблем при проектировании ГЛА является достоверное предсказание параметров тепло-массообмена на его поверхности. Правильное решение этой задачи позволяет уже на стадии проектирования перспективного аппарата оптимизировать его геометрические, траекторные, весовые и прочие параметры, а также определить потребную толщину и материалы в составе теплой защиты летательного аппарата.
Для перспективных ГЛА особенно важно определить тепловые режимы таких наиболее теплонапряженных участков поверхности аппарата, как носок фюзеляжа, передние кромки крыльев, кромки входных устройств и др.
Поскольку в гиперзвуковых летательных аппаратах указанные элементы имеют форму затупленных тел (сфера или цилиндр), то в работе проводилось исследование термо-газодинамических процессов при обтекании сферы гиперзвуковым потоком.
Следует заметить, что процесс обтекания притупленного тела гиперзвуковым потоком на больших высотах полёта (H > 60 км) в связи с большим разрежением атмосферы имеет ряд специфических особенностей. Эти особенности необходимо учитывать при разработке математической модели термо-газодинамических процессов, сопутствующих полёту с гиперзвуковой скоростью. В частности, в таких условиях полёта необходимо проводить анализ на достоверность применимости модели сплошной среды и системы уравнений Навье-Стокса в качестве математической модели газодинамики обтекания тела. Кроме того газ набегающего потока за отошедшей ударной волной (в сжатом и пограничном слоях) теряет свойства идеального. Это значит, что его параметры определяются не только уровнем температуры, но и зависят от давления. При этом особую корректность необходимо выдержать при моделировании объёмных химически неравновесных реакций диссоциации, рекомбинации и частичной ионизации, которые протекают в сжатом и химически активном пограничном слое. Задача ещё более осложняется тем, что в таких условиях гиперзвукового полёта в процессе теплообмена значительное влияние оказывает каталитическая активность поверхности ГЛА. Кроме того при скоростях полёта, превышающих 10 км/сек., важную роль в теплообмене на поверхности ГЛА начинают играть процессы спектрального неравновесного излучения ударной волны и сжатого слоя.
Таким образом, задача обтекания притупленных тел гиперзвуковым потоком сводится к сложной многопараметрической задаче. На основании изложенного, возникла необходимость сопоставления результатов строгого численного моделирования подобных многопараметрических задач с данными, полученными при использовании алгебраических критериальных соотношений [1]. Как известно, в инженерной практике при проектировании ГЛА в расчётах теплообмена всё ещё находит место использование таких соотношений. Всё указанное определяет актуальность данной работы.
1. Постановка задачи.
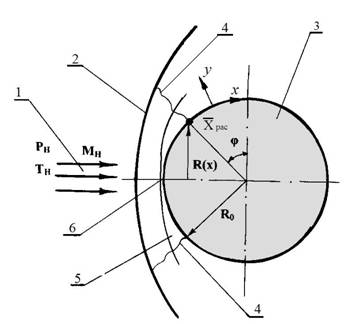
В работе исследовались процессы термо-газодинамики и теплообмена при обтекании гиперзвуковым потоком сферы диаметром 0,06096 м, выполненной из графита с покрытием и без покрытия (рис. 1). Скорость набегающего потока соответствовала числу Маха, М = 29,45. Статические параметры состояния газа в потоке: температура - 196,7 К, давление - 12,21 Па.
Задача решалась в строгой постановке с применением сеточных методов численного моделирования. Расчёт теплообмена на поверхности сферы проводился с учётом каталитической активности поверхности. Рассмотрены два предельных случая. В первом, графитовая поверхность сферы принималась абсолютно каталитической (кw → ∞). Во втором, на поверхности сферы формировалось покрытие, обладающее нулевой каталитической активностью (кw → 0). В том и другом случае поверхность сферы принималась химически нейтральной к компонентам набегающего потока, т.е. поверхность сферы считалась непроницаемой.
|
M∞ = 29,45 P∞ = 12,21 Pa T∞ = 196,7 K
Массовая концентрация молекул: С(O2) = 0,233 C (N2) = 0,767
|
|
Рис. 1. Схема газодинамики обтекания сферы гиперзвуковым потоком:
1- невозмущённый поток, 2- ударная волна, 3- сфера, 4- звуковая линия,
5- пограничный слой, 6- передняя критическая точка.
В научной печати опубликован ряд работ, в которых исследовались процессы термо-газодинамики и теплообмена при обтекании сфер разных диаметров, а также других затупленных тел, в широком диапазоне изменения чисел Маха набегающего потока. Например, в работе [5] опубликованы данные экспериментальных исследований на ударных трубах и сверхзвуковых высокоэнтальпийных газодинамических стендах. В работах [8], [3] и др. опубликованы результаты расчётов численными методами, как с помощью решения дискретных аналогов системы Навье-Стокса, так и с помощью методов прямого статистического моделирования.
Наличие таких данных позволило провести верификацию составленной в данной работе математической модели путём сравнения результатов.
2. Проверка применимости модели сплошной среды
Общеизвестно, что система уравнений Навье-Стокса корректно описывает процессы, проходящие в сплошной среде, континууме. В том случае, если течение реализуется при сильном разрежении набегающего потока, условие континуума может не выполняться. В этой связи при решении задачи следует проводить анализ на достоверность применимости модели сплошной среды к конкретным условиям полёта КЛА. При этом определяющим критерием при проведении анализа является критерий Кнудсена, который, как известно, устанавливает соотношение между средней длиной свободного пробега l частиц в пограничном слое (молекул, атомов и др.) с характерным линейным размером L обтекаемого тела:
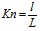. (2.1)
Понятно, что в идеале сплошной является среда, в которой число Кнудсена равно нулю.
В механике сплошной среды установлено, что условие континуума строго выполняется, когда критерий Кнудсена изменяется диапазоне 0 < Kn < 0,03. В этом случае систему уравнений Навье-Стокса можно применять в качестве математической модели, описывающей газодинамику течения. Как известно, в континуальном течении выполняется закон «прилипания», т.е. нормальная и касательная составляющие вектора скорости частиц на поверхности тела равны нулю. В данной работе этот процесс принимается в качестве граничных условий на поверхности обтекаемого потоком тела.
Показано, что применение системы уравнений Навье-Стокса возможно также при, так называемом, режиме переходного течения, которое реализуется в диапазоне изменения критерия Кнудсена 0,03 < Kn < 0,1. Однако в этом случае на стенке равна нулю только нормальная составляющая вектора скорости частиц, поэтому граничные условия видоизменяются, и получили наименование «стенка с проскальзыванием».
В случае если значения критерия Кнудсена превышают 0,1, течение является свободномолекулярным. Такое течение не может корректно описываться математической моделью в виде системы уравнений Навье-Стокса.
Проведенный в данной работе анализ показал, что применительно к изложенным в постановке задачи условиям средняя длина свободного пробега l частиц в сжатом и пограничном слое, примерно, на два прядка величины меньше длины характерного размера обтекаемого тела, т.е. l = 4,88•10-4м, в то время как L = 6,096·10-2м. В итоге критерий Кнудсена оказался равным: Kn = 0,008.
Таким образом, для траекторных параметров полёта КЛА, изложенных в постановке задачи, условие континуальности выполняется, а значит применение системы уравнений Навье-Стокса в сочетании с граничными условиями прилипания на твёрдых стенках вполне оправдано.
3. Термо-газодинамические и теплофизические свойства газа в гиперзвуковой газодинамике.
При решении задач термо-газодинамики и тепло-массообмена в случае внешнего обтекания тел гиперзвуковыми потоками всё еще остро стоит проблемный вопрос достоверного описания свойств газовой среды, формирующей поток.
Известно [2], что при обтекании тела гиперзвуковым потоком в сжатом и пограничном слое, газ становится химически активным. В таком газе реализуются как химические реакции диссоциации молекул на атомы, так и обратные реакции, рекомбинации атомов в молекулы. Наличие этих реакций изменяет механизм переноса теплоты и массы в пограничном слое, т.е. интенсифицирует процессы тепло-массообмена между газовым потоком и поверхностью тела. Уровень критерия Маха, при котором в сжатом и пограничном слоях реализуются эти процессы, определяет газодинамическую природу течения, переводя его их сверхзвукового в гиперзвуковое. При полёте летательного аппарата в воздушной атмосфере начало такого течения соответствует M ≥ 6. Поскольку при гиперзвуковом режиме течения воздух становится химически активным и многокомпонентным, то он переходит в разряд реального газа и все его свойства не подчиняются законам термодинамики идеального газа. Поэтому в условиях гиперзвукового полёта воздух становится многокомпонентным газом и встаёт вопрос о необходимости совместного решения системы уравнений Навье-Стокса с уравнениями Максвелла.
В связи с указанным при условиях полёта КЛА (см. постановку задачи), воздух рассматривался в виде смеси из пяти компонентов (O2, N2, O, N, NO).
При этом парциальная плотность каждой i-ой компоненты воздуха вычислялась с использованием уравнения состояния в виде:
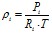(3.1)
где Pi - парциальное давление i-ой компоненты в составе смеси; Ri = Rμ/Mi– газовая постоянная, Rμ – универсальная газовая постоянная, Mi – мольная масса i-го компонента.
Плотность смеси:
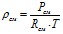, (3.2)
где давление смеси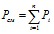 
, Rсм = Rμ/Mсм газовая постоянная смеси, Mсм мольная масса смеси, 
, 
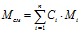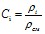–массовая концентрация i-ой компоненты в смеси;
Термодинамическая энтальпия смеси:
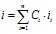, (3.3)
где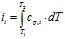 
– термодинамическая энтальпия i-ой компоненты.
Удельная теплоёмкость сp,i каждой i-ой компоненты задавалась по кусочно-линейному закону в виде функции от температуры и давления. В результате средняя удельная теплоёмкость газовой смеси вычислялась с использованием соотношения:
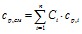, (3.4)
где: Ci– массовая концентрация каждого компонента;
сp,i – удельная изобарная теплоёмкость каждого компонента.
Теплопроводность λi каждой i-ой компоненты вычислялась с использованием соотношения из кинетической теории газов:
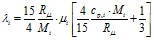, (3.5)
где: Rμ - универсальная газовая постоянная;
Mi - мольная масса i-го компонента;
μi - динамическая вязкость i-го компонента;
cpi - удельная изобарная теплоёмкость i-го компонента.
Теплопроводность газовой смеси вычислялась по формуле:
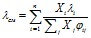(3.6)
где: Xi - мольная концентрация i-го компонента; λi - теплопроводность i-го компонента; параметр φi j рассчитывался с использованием соотношения:
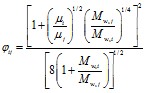(3.7)
Вязкость каждого i-го компонента вычислялась по известной формуле Сатерленда в виде:
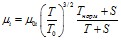(3.8)
где: μ0i – динамическая вязкость i-го компонента при нормальных условиях;
T – статическая температура, К;
Tнорм –температура при нормальных условиях;
S– эффективная температура (константа Сатерленда).
Динамическая вязкость газовой смеси вычислялась следующим образом:
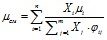(3.9)
где: Xi - мольная концентрация компонента i;
μi - вязкость компонента i;
Следует отметить, что при высоких температурах результаты расчёта по формуле Сатерленда (3.8) несколько отличаются от известных табличных данных [6]. Однако применение формулы в первом приближении можно считать вполне оправданным.
Кроме того для каждого компонента смеси задавалась значения энтропии и энтальпии при нормальных условиях.
Для вычисления коэффициента бинарной диффузии использовалось модифицированное соотношение Чемпена-Энскога.
При расчёте лучистого теплообмена коэффициент поглощения для газовой среды вычислялся как функция температуры с учётом свойств каждого i-го компонента по закону для смеси серых газов [7].
4. Математическая модель обтекания сферы гиперзвуковым потоком.
В целях экономии расчётных ресурсов задача решалась в двухмерной, (осесимметричной) постановке. То есть рассматривалось только одно меридиональное сечение сферы. При этом принималось, что течение во всех меридиональных сечениях идентично.
Решались дискретные аналоги системы уравнений Навье-Стокса для модели вязкой сжимаемой теплопроводной среды, а также уравнение модели переноса излучения и уравнение теплопроводности для твёрдого тела.
Как уже отмечалось ранее, газовая среда задавалась смесью из пяти компонентов. Эффекты диссоциации и рекомбинации учитывались с помощью модели конечной скорости химической реакции. Так как при гиперзвуковых скоростях потока характерный временной масштаб потока подобен временному масштабу протекания химических процессов, то применялась модель неравновесной химии.
Для воздуха при высоких температурах известно довольно большое количество схем моделей механизмов химической кинетики. Используются, например, схема Или-Райдила, схема Ленгмюра-Хиншельвуда и др. В рамках данной работы рассматривалась модель, состоящая из пяти основных неравновесных химических реакций, три из которых реализуются с участием третьих тел (М) (Таблица 1).
Таблица 1
|
1 |
O2+M⇔2O+M |
|
2 |
N2+M⇔2N+M |
|
3 |
NO+M⇔N+O+M |
|
4 |
NO+O⇔O2+N |
|
5 |
N2+O⇔NO+N |
Для каждого из компонентов газовой смеси решалось отдельное уравнение переноса массы в виде:
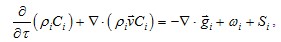, (4.1)
Сi– локальная массовая концентрация i-го компонента;
gi – диффузионный поток i-го компонента;
В уравнении (4.1)члены слева направо представляют: нестационарность процесса переноса массы, перенос массы конвекцией, перенос массы диффузией, источник массы, обусловленный наличием химических реакций, прочие источники массы.
В представленном уравнении:
ωi–скорость образования i-го компонента в химических реакциях;
Si - скорость образования i-го компонента за счёт наличия дополнительных источников;
Скорость образования i-го компонента в химических реакцияхωi.вычисляется с использованием соотношения вида:
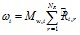(4.2)
где: Mw,i – мольная масса i-го компонента;
NR – количество химических реакций в расчёте;
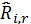– мольная скорость образования (распада)i-го компонента в реакции r, вычисленная по уравнению химической кинетики скорости образования i-го компонента в ходе неравновесной химической реакции.
Для неравновесной химической реакции молярная скорость образования (распада)i-го компонента в реакции r, записывается в виде:
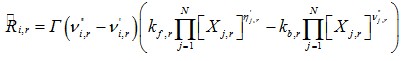(4.3)
Xj,r - мольная концентрация компонента j в реакции r (Кмоль/м3);
η'j,r - показатель степени для реагента j в реакции r;
ν'j,r - стехиометрический коэффициент для реагента j в реакции r;
ν''j,r - показатель степени для продукта j в реакции r (всегда равен стехиометрическому коэффициенту продукта реакции);
Г- коэффициент, учитывающий влияние третьих тел на скорость реакции;
kf,r - константа скорости прямой реакции;
kb,r - константа скорости обратной реакции.
В уравнении (4.3) коэффициент Г, учитывающий влияние третьих тел на скорость химической реакции, вычислялся следующим образом:
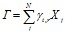(4.4)
где: γj,r - эффективность компонента j в реакции r как третьего тела;
Xj - мольная концентрация компонента j.
Эффективность каждого химического компонента в качестве третьего тела представлена в таблице 2.При этом за единицу принята эффективность аргона.
Таблица 2
|
№ реакции |
O2 |
N2 |
NO |
N |
O |
|
1 |
5 |
2 |
2 |
2 |
25 |
|
2 |
2 |
5 |
2 |
3 |
5 |
|
3 |
2 |
2 |
2 |
5 |
5 |
Константа скорости каждой прямой или обратной реакции r вычислялась по выражению типа Аррениуса (f - прямая реакция, b - обратная реакция):
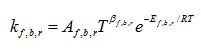(4.5)
где: Af,b,r - предэкспоненциальный фактор;
βf,b,r - температурный показатель;
Ef,b,r - энергия активации реакции;
R - универсальная газовая постоянная.
Для вычисления константы скорости каждой реакции применялись эмпирические коэффициенты, приведённые в таблице 3.
Таблица 3
|
№ реакции |
Af,r |
βf,r |
Ef,r |
Ab,r |
βb,r |
Eb,r |
|
1 |
2.5005e+13 |
-0.5 |
4.9365e+08 |
8.90e+11 |
-0.44 |
0.0 |
|
2 |
2.0004e+18 |
-1.5 |
9.4177e+08 |
1.91e+17 |
-1.57 |
0.0 |
|
3 |
5.5042e+17 |
-1.5 |
6.2782e+08 |
1.67e+17 |
-1.52 |
0.0 |
|
4 |
3.1999e+06 |
1.0 |
1.6365e+08 |
2.67e+07 |
0.92 |
2.9486e+07 |
|
5 |
6.8027e+10 |
0.0 |
3.1395e+08 |
2.10e+10 |
-0.04 |
0.0 |
В правую часть уравнения энергии для того, чтобы учесть процесс образование и поглощение тепловой энергии был введён член - источник энергии Sh. В результате, уравнение приняло следующий вид:
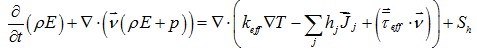(4.6)
В свою очередь, член - источникShможет быть представлен в виде:
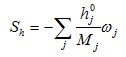(4.7)
где: ωj - скорость образования компонента j;
Mj - мольная масса компонента j;
h0j - энтальпия образования компонента j.
Для решения системы уравнений Навье-Стокса, а также уравнений конвекции и диффузии применён так называемый связанный решатель. То есть основные уравнения решались в виде единого связанного набора. Уравнения дополнительных моделей решались отдельно от связанного набора и последовательно, одно за другим.
Для имитации лучистого теплообмена применялась модель дискретных ординат в её классической формулировке [4], которая обеспечивает получение достоверных данных по уровню лучистых тепловых потоков в задачах с оптически тонкими средами. Эта модель представляется уравнением лучистого переноса.
Поверхность сферы считалась полностью непрозрачной с диффузным отражением и коэффициентом черноты εw = 0.8.
В объёме с целью определения температурного поля решалось основное дифференциальное уравнение теплопроводности с граничными условиями 3-го рода. В результате, получены поля температуры в объёме сферы, а также распределение температуры по её поверхности.
5. Анализ влияния структуры расчётной сетки на результаты решения задачи.
Уравнения механики сплошной среды и всех дополнительных моделей решались на структурированной расчётной сетке, состоящей из 22304 четырёхугольных ячеек (рис.2.1).
а) общий вид структурированной расчётной сетки.
б) область исследуемого тела
Рис.2.1. Исходная расчётнаясетка
В том случае, если в потоке возникают скачки уплотнения, для получения достоверных расчётных данныхпринципиально важноиспользовать сетку высоким разрешениемв области больших градиентов температуры и давления. По этой причине в работе исходная сетка была адаптированадля расчёта с помощьюметодаразбиения с созданием висячих узлов. При его использовании ячейка, помеченная для адаптации, разбивается на 4 новые ячейки. В результате появляются новыевисячие узлы, то есть сетка становится неконформной. Параметрыв уже существующих узлах распространяются на новые узлы с помощью метода интерполяции. В данном случае измельчались ячейки, градиент статической температуры в которых был больше 3.5% от максимального градиента статической температуры в потоке. В каждом расчёте адаптация применялась два раза.
Расчётная сетка после первой адаптации увеличилась на 17.5% и составила приблизительно 26000ячеек, а после второй адаптации ещё на 35% и составила приблизительно 35000ячеек. Дальнейшее измельчение сетки не применялось по причине её чрезмерного разрастания. Расчётная сетка вблизи исследуемой сферы показана на рисунке2.2 (а – после адаптации №1; б – после адаптации №2).
а) адаптация №1
б) адаптация №2
Рис.2.2. Адаптированная расчётная сетка
Использование метода адаптации расчётных сеток вызывает необходимость проводить анализ влияния структуры расчётной сетки на результаты решения задачи, а также определить оптимальное количество адаптаций, которое необходимо для получения более достоверных данных.
Выводы
1. Предложена математическая модель процессов термо-газодинамики и теплообмена, реализуемых при обтекании сферы – элемента конструкции ГЛА воздушным гиперзвуковым потоком. [2]
2. Проведён анализ влияния структуры расчётной сетки на результаты решения задачи, проведена также её адаптация для расчёта математической модели методом разбиения с созданием висячих узлов.
Работа выполнена при поддержке РФФИ, грант № 13-08-01328 а.
Рецензенты:
Молчанов А.М., д.т.н., доцент Московского авиационного института (национального исследовательского университета), г. Москва.
Никитин П.В., д.т.н., профессор Московского авиационного института (национального исследовательского университета), г. Москва.
[2] Результаты решения представленной математической модели численным методом и её верификация изложены в статье, которая будет опубликована в следующем номере данного журнала.