Введение
Что такое сайт и гиперссылка сегодня известно всем, но поскольку для этих понятий можно дать много разных определений, уточним, что понимается под ними в данной статье.
Веб-сайт (сайт) – это совокупность взаимосвязанных html-страниц и веб-документов, связанных внутренними гиперссылками и обладающих единством содержания, идентифицируемый в Вебе по его доменному имени.
На различных страницах одного сайта могут встречаться гиперссылки на один и тот же внешний адрес, имеющие одинаковый контекст (в частном случае – анкор) и количество таких «одинаковых» гиперссылок может быть равно количеству страниц на сайте (например – ссылка на сайт вышестоящей организации). Из множества гиперссылок с одинаковым адресом-приёмником и контекстом, сделанных с данного сайта, мы будем рассматривать только одну, т.н. «уникальную» – ту, которая находится на странице, имеющей максимальный уровень (наивысшим считается уровень начальной страницы сайта). Поскольку далее рассматриваются только такие ссылки, мы будем называть их гиперссылками (или просто ссылками).
На сегодняшний день каждая солидная организация имеет собственный сайт, и зачастую не один. Среди множества сайтов организации можно выделить её официальный сайт и другие сайты (например, для научного учреждения это сайты его лабораторий, проводимых конференций, персональные сайты сотрудников и т.д.). Под веб-пространством организации будем понимать множество веб-сайтов данной организации, связанных посредством гиперссылок. Далее для краткости веб-пространство организации будем называть термином «пучок» (от англ. bunch).
Рассмотрим тематический фрагмент Веба, состоящий из веб-сайтов организаций с однотипной деятельностью. (Например, продолжая тему научных учреждений, это могут быть веб-сайты РАН.) Одним из важных вопросов вебометрики является вопрос о том, насколько связным является такой фрагмент Веба. Понятно, что связность на множестве пучков должна возрасти по сравнению со связностью фрагмента, построенного только на официальных сайтах. Нас интересует вопрос количественной оценки того, насколько сильно влияют на связность фрагмента Веба сайты организаций, не являющиеся их официальными сайтами.
В статье описывается проведение такого исследования на примере научных учреждений РАН (точнее, до принятия Распоряжения Правительства Российской Федерации от 30 декабря 2013 г. [4] входивших в состав РАН). Изложенный подход представляется достаточно универсальным и легко переносимым на любые тематические фрагменты Веба.
Основные понятия и инструменты исследования
В общем случае веб-графом называется ориентированный граф, множество вершин которого соответствует множеству страниц в Вебе, а множество дуг – множеству гиперссылок, связывающих эти страницы. Рассматривая все страницы одного веб-сайта как единое целое и соответствующим образом агрегируя гиперссылки, можно получить веб-граф, построенный на некотором множестве сайтов.
Зададим веб-граф тематического фрагмента Веба следующим образом. Пусть вершины графа соответствуют всем сайтам организаций (как официальным, так и другим), а множество дуг строится по следующему правилу: дуга из вершины А в вершину B существует тогда, когда существует хотя бы одна гиперссылка с сайта, соответствующего вершине А на сайт, соответствующий вершине B. Понятно, что такой веб-граф является ориентированным графом без петель и кратных рёбер. При этом его достаточно для оценки связности тематического фрагмента Веба.
На рис. 1 в левой части приведен пример веб-графа тематического фрагмента Веба для трех организаций. Официальные сайты организаций обозначены разными геометрическими фигурами большого размера. Соответствующие фигуры меньшего размера обозначают другие сайты организаций. Для удобства восприятия веб-пространство каждой организации обведено пунктиром.
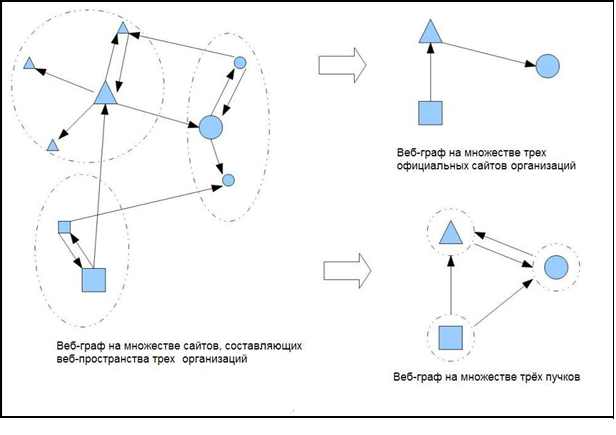
Рис. 1. Веб-графы для сайтов трех организаций
Если ограничить множество вершин в графе только официальными сайтами, то получим веб-граф на множестве официальных сайтов организаций (на рис. 1 переход вправо по верхней стрелке). Если же в качестве множества вершин взять множество пучков организаций, а в качестве множество дуг взять только гиперссылки, связывающие пучки, а гиперссылки, связывающие сайты внутри пучка не принимать во внимание, то получим веб-граф на множестве пучков (на рис. 1 переход вправо по нижней стрелке). В нашем примере на рис. 1 связность веб-графа на пучках существенно выше, чем множества веб-графа на официальных сайтах за счёт связей, имеющихся между другими сайтами организаций.
Для построения веб-графов реального фрагмента Веба используются данные о гиперссылках из базы данных внешних гиперссылок, разрабатываемой в Институте прикладных математических исследований КарНЦ РАН [2]. Гостевой доступ к базе реализован по ссылке http://grid.krc.karelia.ru/webometrics2 (Имя пользователя: guest, Пароль: guest). В настоящее время в базе хранятся данные о 334 тысячах внешних гиперссылок, сделанных с 1400 веб-сайтов вузов и научных учреждений России и зарубежья.
Для анализа веб-графов используется открытая программная платформа Gephi [6].
Исследование фрагмента Веба научных организаций
В качестве исследуемых организаций взяты 397 научных учреждений (до реформы РАН они назывались «научными учреждениями РАН»): собственно РАН, отделения по областям науки, региональные отделения и научные центры, научные институты. Для идентификации сайта используется его название и/или доменное имя, например, Институт прикладных математических исследований КарНЦ РАН (mathem.krc.karelia.ru). Все 397 научных учреждений имеют официальный сайт 145 учреждений, по крайней мере, еще 1 сайт (лаборатории, конференции, проекта, журнала) с доменным именем, являющимся поддоменом домена головного сайта (в данном исследовании это верно почти всегда, за редким исключением; тогда это сайты, которые либо очень хорошо известны, либо «попутно» найдены в процессе исследования). Общее количество исследуемых сайтов научных учреждений равно 956. Полный список исследуемых сайтов можно увидеть на сайте проекта «Вебометрический рейтинг научных учреждений России» [1] в разделе «Целевое множество».
В таблице 1 приводятся характеристики веб-графов, построенных на различных множествах сайтов научных учреждений. Обратим внимание на незначительное увеличение количества дуг в веб-графе на множестве пучков по сравнению с веб-графом на множестве официальных сайтов (всего на 177). Это значит, что веб-сайты, не являющиеся официальными, в основном ссылаются на сайты в рамках своих же веб-пространств организаций.
Таблица 1. Основные характеристики веб-графов
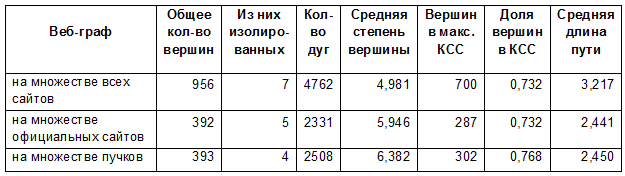
При этом увеличение количества вершин в максимальной КСС на 5 % нельзя считать незначительным, поскольку максимальная КСС на множестве официальных сайтов, содержащая более 73 % всех вершин, уже является достаточно большой и её прирост и не должен быть большим. Интересно, что средняя длина пути при этом немного возросла. По-видимому, это связано с тем, что вершины, вошедшие в КСС, удлинили максимальный путь до произвольной вершины. Тем более что в КСС вошла одна вершина, которая ранее вообще была изолированной.
Первая десятка по показателю Page Rank [5], довольно часто используемого для характеристики значимости вершин, показана в таблице 2.
Таблица 2. Значения Page Rank
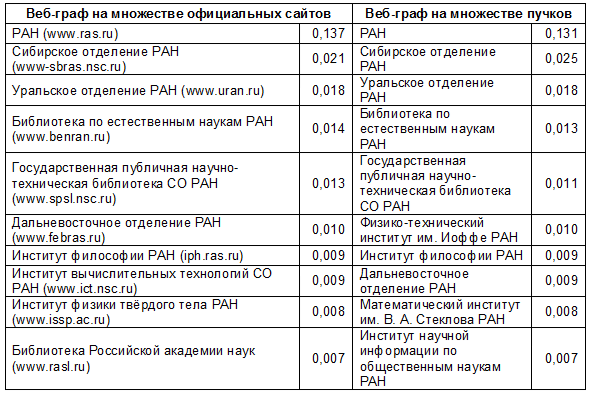
Как видим, и в том и другом случае в первую десятку попали по 7 научных учреждений, а первая пятерка полностью совпадает. Тенденция сохраняется и далее при рассмотрении выборок большего размера, к примеру, для списка из первых 20 учреждений совпадение наблюдается по 16 из них, а первая десятка из таблицы 2 совпадает полностью.
Изменение позиции учреждения по PR невозможно объяснить каким-либо одним фактором, но наличие большого количества сайтов в пучках, несомненно, оказывает решающее значение. К примеру, попадание в первую десятку Физико-технического института им. Иоффе РАН (www.ioffe.ru) объясняется как наличием еще пяти сайтов этого учреждения, составляющим, в дополнение к официальному сайту, веб-пространство института. И при этом надо отметить высокую инцидентность добавленных сайтов, например, сайт The journals published by Ioffe Institute (journals.ioffe.ru), имея немного исходящих ссылок на другие научные сайты, имеет много входящих. В то же время Математический институт им. В.А. Стеклова РАН (www.mi.ras.ru) имеет веб-пространство, состоящее из 20 сайтов, которые за существенно повышают инцидентность вершины, соответствующей институту, в веб-графе на множестве пучков.
Заключение
Проведенное исследование связности научных учреждений является в некотором смысле сопутствующим исследованием по отношению к проекту «Вебометрический рейтинг научных учреждений России» [1]. Одним из индикаторов, используемом в этом проекте, является так называемая «внутренняя популярность веб-ресурсов научного учреждения», вычисляемая как произведение количества гиперссылок, сделанных на все сайты учреждения, на количество учреждений, с веб-ресурсов которых сделаны эти ссылки. Сайты и ссылки в рамках одного пучка при этом не учитываются.
Понятно, что такие характеристики как связность веб-графов и PR вершин хотя бы и косвенно показывают, насколько велики изменения в веб-графе на пучках по сравнению с веб-графом на официальных сайтах.
По результатам исследования, описанным в статье, можно сделать вывод о том, что в целом существенных изменений при переходе от официальных сайтов к пучкам ожидать не приходится. Этот результат подтверждает предварительный вывод, сделанный в работе [3]: «… Сайты множества ближайших окрестностей …. слабо влияют на связность целевого множества, поскольку в основном содержат только гиперссылки, сделанные на головные сайты своих организаций, входящих в целевое множество». Здесь термин «ближайшая окрестность» означает сайты пучка за исключением официального сайта.
Вместе с тем, можно утверждать, что создание новых самостоятельных веб-сайтов организации, имеющих большую значимость в научном сообществе, таких как сайты конференций, журналов, электронных библиотек, повышает присутствие научного учреждения в Вебе, а значит, положительно влияет на его позиции в различных рейтингах и ранжированиях. Вопрос заключается не только в том, насколько ценен веб-сайт, но и в том, насколько он известен. А известность достигается не только благодаря контенту, дизайну, удобству для пользователей, но и «раскруткой» сайта. Совершенно упрощая эту мысль можно сказать, что если у Вас есть веб-сайт проекта, то не забудьте написать его интернет-адрес на своей визитной карточке вместе с адресом официального сайта Вашего института.
Работа выполнена при поддержке гранта РГНФ № 12-03-12001.
Рецензенты:
Кириллов А.Н., д.ф.-м.н., доцент, ведущий научный сотрудник лаборатории моделирования природно-технических систем Института прикладных математических исследований Карельского научного центра РАН, г. Петрозаводск.
Рогов А.А., д.т.н., профессор, заведующий кафедрой теории вероятностей и анализа данных Петрозаводского государственного университета, г. Петрозаводск.



