Проблема повышения качества образования и оценивания качества обучения в вузах является актуальной для современного инженерного образования [3-6, 8].
В условиях модернизации высшей школы и в связи с введением федеральных государственных образовательных стандартов (ФГОС) высшего профессионального образования (ВПО) третьего поколения одним из самых важных является вопрос о методах оценки результатов обучения студентов, их анализе на различных этапах освоения основных образовательных программ: предварительный контроль (учет итогового рейтинга обучающихся на предшествующем этапе обучения), текущий контроль успеваемости (контрольных работ и промежуточных аттестаций) обучающихся и итоговый контроль (в форме рейтинговой системы оценок и их дальнейшим переводом в экзаменационную или зачетную оценку. Основой контроля качества образования является мониторинг [2, 7] или непрерывный контроль, постоянное отслеживание результатов образования, что необходимо для систематической корректировки проводимых мероприятий по их реализации. Мониторинг становится не просто инструментом оценки качества ВПО, а средством управления этим качеством, позволяющим влиять на эффективность управления образовательным процессом. В процессе мониторинга проводились измерения следующих показателей образовательной деятельности студентов в соответствии с ФГОС ВПО:
ВК – результаты входного тестирования по математике в начале текущего семестра,
АТТ1 – результаты 1-ой аттестации по математике в середине текущего семестра,
АТТ2 – результаты 2-ой аттестации по математике в конце текущего семестра,
ЭКЗ – результат классического экзамена в конце текущего семестра,
ЭКЗ* – скорректированные результаты ЭКЗ в середине следующего семестра.
После деления числовых результатов на соответствующий максимксимально возможный рзультат и умножения на пять все результаты были приведены к единой 5-балльной шкале. Таким образом для статистического анализа данных в MS Excel была создана база данных, которая обрабатывалась затем в пакете Statistica [9].
В работе [1] проведен компьютерный статистический сравнительный анализ результатов различных форм контроля заочного обучения студентов вузов. В данной работе представлен дисперсионный анализ динамики результатов изучения высшей математики студентами очной формы обучения трех потоков Физико-технического института (ФТИ) Томского политехнического университета (10 учебных ,объем выборки n =175) , имевших более 25% должников по результатам ЭКЗ по высшей математике в объеме 1-го семестра (линейная алгебра и аналитическая геометрия + дифференциальное исчисление).
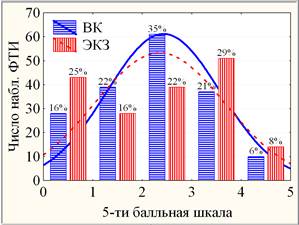
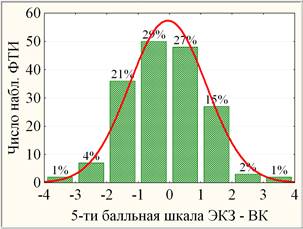
Для корректного применения F-критерия параметрического дисперсионного анализа необходимо предварительно оценить сходства наблюдаемых распределений (гистограмм), например, ВК, ЭКЗ и ЭКЗ – ВК (рис. 1) с теоретическим распределением по нормальному закону (соответствующие кривые).
|
|
|
Рис. 1. Составная гистограмма ВК и ЭКЗ (слева) и ЭКЗ – ВК (справа) ФТИ с соответствующими кривыми нормальных распределений
Проверка нормальности распределений выборок с помощью χ2-критерия Пирсона дает незначимое (уровень значимости р > 0,10) для ВК и ЭКЗ – ВК, но высоко значимое (р < 0,0005) для ЭКЗ отличия наблюдаемых распределений от нормального закона. В связи с нарушением в разной степени условия нормальности распределения выборок далее применялся также и непараметрический дисперсионный анализ.
Заметим, что, согласно теории измерительных шкал, балльная шкала относится к типу порядковых шкал, позволяющих ранжировать (упорядочить) результаты оценивания качества усвоения знаний студентов. В связи с этим для сравнения рассматриваемых выборок предлагается использовать наряду с параметрическими также и ранговые (непараметрические) критерии, основанные на рангах, а не на средних значениях.
Совместное распределение ВК и ЭКЗ (рис. 1) может быть использовано также для визуальной оценки их различия по 5-ти балльной равномерной шкале: положительная динамика (ЭКЗ > ВК) в диапазоне (0, 1]È(3, 5] и отрицательная – в (1, 3], а также общая отрицательная динамика (результаты ЭКЗ – ВК > 0 составляют 45%) несмотря на то, что к ЭКЗ студент готовился, а ВК проводился без предупреждения. При этом на уровне средних выборок mЭКЗ – mВК ≈ 2,3394 – 2,4157 ≈ -0,0763 = mЭКЗ-ВК по 5-ти балльной шкале. Отметим существенный разброс значений разности результатов ЭКЗ – ВК, что свидетельствует об отсутствии значимой корреляции между ВК и ЭКЗ.
Динамика успеваемости ФТИ в переменных {ВК, АТТ1, АТТ2, ЭКЗ, ЭКЗ*} приведена на рис. 2.
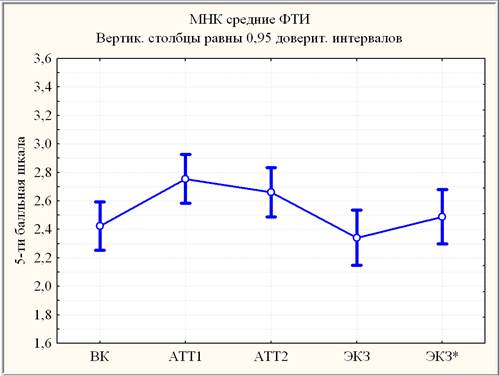
Рис. 2. Динамика успеваемости ФТИ на уровне средних
Для оценки значимости динамики успеваемости ФТИ применен прежде всего (с учетом проверки выборки поэлементной разности ЭКЗ – ВК на нормальность распределения) параметрический дисперсионный анализ повторных измерений. Параметрический F– критерий для зависимых выборок приводит к выводу о высоко значимой (р < 0,0005) динамики успеваемости ФТИ по совокупности показателей {ВК, АТТ1, АТТ2, ЭКЗ, ЭКЗ*}. Применение непараметрического (рангового) дисперсионного анализа Фридмана с повторными измерениями подтвердило результаты параметрического дисперсионного анализа повторных измерений. В рамках параметрического дисперсионного анализа на основании критериев множественного сравнения сделан вывод о незначимом различии (уровень значимости р > 0,10) между АТТ1 (mАТТ1 ≈ 2,727) и АТТ2 (mАТТ1 ≈ 2,655), а также между ЭКЗ (mЭКЗ ≈ 2,339) и ВК (mВК ≈ 2,416) или ВК (mВК ≈ 2,416) и ЭКЗ* (mЭКЗ* ≈ 2,493). При этом различие между ВК и АТТ1 оценивается как высоко значимое (р < 0,0005), между ВК и АТТ2 – сильно значимые (0,0005 < р < 0,005), а между ЭКЗ и ЭКЗ* или ЭКЗ* и АТТ2 – статистически значимые (0,005 < р < 0,05). Полученные результаты подтверждаются ранговым критерием Вилкоксона для зависимых выборок.
Более детальная гистограммная динамика ФТИ в переменных {ВК, АТТ1, АТТ2, ЭКЗ, ЭКЗ*} приведена на рис. 3.
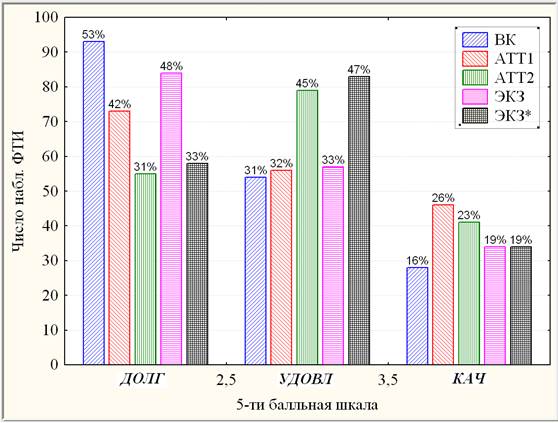
Рис. 3. Составная гистограммная динамика успеваемости ФТИ
Согласно рис. 3, на лицо положительная текущая динамика успеваемости {ВК, АТТ1, АТТ2}: убывание ДОЛГ и рост как УДОВ, так и КАЧ, а также положительная динамика периода после экзаменационной ликвидации задолженностей {ЭКЗ, ЭКЗ*}: убывание ДОЛГ и рост УДОВ. Отрицательная динамика успеваемости экзаменационного периода {АТТ2, ЭКЗ}, проявившаяся, в основном, в росте ДОЛГ и убывании УДОВ, объясняется естественной сложностью итоговой (ЭКЗ) контрольной для слабых студентов.
Выборки {ВК, АТТ1, АТТ2, ЭКЗ, ЭКЗ*} разных форм контроля успеваемости ФТИ являются составными, состоящими из 10-ти учебных групп.
С одной стороны, аналогично динамике успеваемости ФТИ на институтском уровне (рис. 2) можно оценить групповую динамику успеваемости ФТИ (рис. 4). Групповая динамика успеваемости ФТИ является очень пестрой:
- 41, 42, Б1 – значимая (р < 0,05) положительная начальная динамика {ВК, АТТ1}с последующим стабильным уровнем,
- 72, А3 – значимая положительная начальная динамика {ВК, АТТ1}с последующей отрицательной {АТТ1, АТТ2, ЭКЗ},
- А1, А2, А4 – незначимая начальная динамика {ВК, АТТ1}с последующей отрицательной { АТТ, ЭКЗ},
- Д1 – незначимая динамика, А5 – значимая переменная динамика.
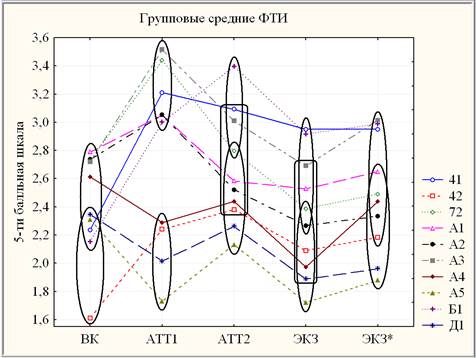
Рис. 4. Групповая динамика успеваемости ФТИ.
С другой стороны, применение F-критерия дисперсионного анализа для независимых выборок приводит к выводу о высоко значимой неоднородности (на уровне значимости р < 0,0005) результатов АТТ1 и статистически значимой неоднородности (0,005 < р < 0,05) результатов ВК, АТТ2, ЭКЗ, ЭКЗ* по совокупности групп. Заметим, что непараметрические альтернативы однофакторного дисперсионного анализа для независимых выборок (критерий Краскела-Уоллиса и медианный тест) подтверждают сделанный на основе F-критерия вывод об уровне значимости неоднородности АТТ1, АТТ2 и смягчают значимость неоднородности ВК, ЭКЗ, ЭКЗ* до слабой (0,05 < р < 0,10). Уровень значимости различий между групповыми средними можно оценить с помощью апостериорного критерия наименьших значений разности, согласно которому можно оформить однородные (различающиеся незначимо) кластеры групповых средних в порядке их убывания для каждого показателя (рис. 4):
ВК: {А1, А2, 72, А3, А4, Д1, А5, 41, Б1}, {Д1, А5, 41, Б1, 42} так, что 42 отличается от Д1 слабо значимо (0,05< р < 0,10), а от А4 – статистически значимо (0,005< р < 0,05);
АТТ1: {А3, 72, 41, А1, А2, Б1}, {А4, 42, Д1, А5} так, что А3 от А4 или А5 от Б1 отличаются сильно значимо (0,0005< р < 0,005), а А4 от Б1 – слабо значимо (0,050< р < 0,100);
АТТ2: {Б1, 41, А3, 72}, {41, А3, 72, А1, А2, А4, 42}, {72, А1, А2, А4, 42, Д1, А5} так, что Б1 от А1 или 41 от Д1, а также А5 от А3 отличаются статистически значимо (0,005< р < 0,05);
ЭКЗ: {41, Б1, А3, А1, 72, А2}, {А3, А1, 72, А2, 42, А4, Д1}, { 72, А2, 42, А4, Д1, А5}, так, что 41 от 42 или А5 от А1 отличаются статистически значимо (0,005< р < 0,05);
ЭКЗ*: {А3, Б1, 41, А1, 72, А4, А2, 42}, { А1, 72, А4, А2, 42, Д1, А5} так, что А3 от Д1 или А5 от 41 отличаются статистически значимо (на уровне значимости 0,005< р < 0,05).
По результатам образовательного мониторинга ФТИ можно сформулировать следующие предложения по повышению качества успеваемости студентов:
- Усиление работы приемной комиссии по повышению качества набора в силу низких результатов ВК (53% набора имеют «неуд» на рис. 3).
- Увеличение аудиторных часов на изучение сложной программы высшей математики в силу слабо «удовл» результатов текущего контроля (рис. 2-4).
- Введение составной итоговой отчетности по высшей математике в объеме 1-го семестра в связи с составным характером семестровой программ: линейная алгебра и аналитическая геометрия (зачет) + дифференциальное исчисление (экз) для ликвидации разрыва АТТ2-ЭКЗ (рис. 2-4). Зачет по первой теме можно провести в середине семестра в рамках конференц-недели.
- Продление периода ликвидации задолженностей за семестр {ЭКЗ, ЭКЗ*} возможно в зимней и летней школе, дающей возможность доосвоить сложную программу высшей математики и имеющей положительную динамику (рис. 2-4).
Выводы
- В рамках параметрического дисперсионного анализа повторных измерений оценена динамика успеваемости ФТИ на институтском уровне: сделан вывод о незначимом различии (уровень значимости р > 0,10) между АТТ1 (mАТТ1 ≈ 2,727) и АТТ2 (mАТТ1 ≈ 2,655), а также между ЭКЗ (mЭКЗ ≈ 2,339) и ВК (mВК ≈ 2,416) или ВК (mВК ≈ 2,416) и ЭКЗ* (mЭКЗ* ≈ 2,493). При этом различие между ВК и АТТ1 оценивается как высоко значимое (р < 0,0005), между ВК и АТТ2 – сильно значимые (0,0005 < р < 0,005), а между ЭКЗ и ЭКЗ* или ЭКЗ* и АТТ2 – статистически значимые (0,005 < р < 0,05).
- Применение непараметрического (рангового) дисперсионного анализа Фридмана с повторными измерениями подтвердило результаты параметрического дисперсионного анализа повторных измерений.
- На основании дисперсионного анализа для независимых выборок сделан вывод о высоко значимой неоднородности (на уровне значимости р < 0,0005) результатов АТТ1 и статистически значимой неоднородности (на уровне значимости 0,005 < р < 0,05) результатов ВК, АТТ2, ЭКЗ, ЭКЗ* по совокупности групп. Оформлены однородные (различающиеся незначимо) кластеры групповых средних в порядке их убывания для каждого показателя.
- Непараметрические альтернативы однофакторного дисперсионного анализа для независимых выборок (критерий Краскела-Уоллиса и медианный тест) подтверждают сделанный на основе F-критерия вывод об уровне значимости неоднородности АТТ1, АТТ2 и смягчают значимость неоднородности ВК, ЭКЗ, ЭКЗ* до слабой (0,05 < р < 0,10) по совокупности групп.
- По результатам образовательного мониторинга ФТИ формулированы предложения по повышению качества успеваемости студентов.
Работа выполнена при поддержке Российского научного фонда.
Рецензенты:
Трифонов А.Ю., д.ф.-м.н., профессор кафедры высшей математики и математической физики, ФГБОУ ВПО «Национальный исследовательский Томский политехнический университет, г. Томск.
Арефьев К.П., д.ф.-м.н., профессор кафедры высшей математики, ФГБОУ ВПО «Национальный исследовательский Томский политехнический университет, г. Томск.