Рассмотрим периодическую краевую задачу для дифференциального уравнения первого порядка, не разрешенного относительно производной
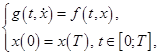(1)
где функции 
и предполагается, что функция 
непрерывна, функция 
удовлетворяет условию Каратеодори.
Пусть 
- пространство непрерывных на отрезке 
функций, 
– пространство измеримых ограниченных в существенном на отрезке функций, 
- пространство непрерывно дифференцируемых на отрезке функций с нормой
.
Под решением понимается такой элемент пространства , который почти всюду удовлетворяет уравнению и краевому условию задачи (1).
В работе доказывается существование решения задачи (1) в шаре радиуса 
с центром в точке 
пространства . С помощью метода явной линеаризации задача (1) сводится к квазилинейной краевой задаче, для доказательства существования решения которой применяется теорема из работы [8].
Будем рассматривать задачу (1) в предположении, что существует такая функция 
, удовлетворяющая условиям:
- для каждого фиксированного 
на искомом шаре с центром в точке 
пространства выполняется неравенство: 
(данное условие предполагает, что функция 
должна удовлетворять условию 
);
- оператор 
, определенный равенством: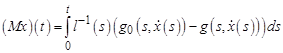 
,
является вполне непрерывным оператором.
Некоторые математические модели реальных процессов приводят к задачам для обыкновенных дифференциальных уравнений, не разрешенных относительно старшей производной, и в частности к задаче (1). Обычно при исследовании нелинейных задач, в том числе и задачи (1), используется явная или неявная линеаризация. В частности, в работах [4; 6; 9] используется редукция нелинейной задачи к некоторой вспомогательной квазилинейной, к которой применяются известные схемы исследования на разрешимость квазилинейных или резонансных краевых задач. К числу методов, использующих неявную линеаризацию нелинейных задач, можно отнести метод Ньютона-Канторовича, метод применения теорем о неявной функции, методы теории нелинейных фредгольмовых операторов. В этом случае нелинейный оператор аппроксимируется своей производной [2; 3; 5; 10].
Как уже было указано ранее, в работе используется первый подход. Отметим, что в отличие от ранее цитируемых работ в настоящей работе предполагается, что нелинейную задачу для дифференциального уравнения первого порядка, не разрешенного относительно производной, можно записать в виде (1) и что существует такая функция , для которой выполняется неравенство . Помимо этого, в работе используется подход, предложенный автором [1] для доказательства разрешимости квазилинейных краевых задач в случае резонанса.
Обозначим через 
, при этом будем предполагать, что функция 
на отрезке . Существование такой функции позволяет задачу (1) переписать в виде
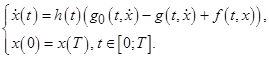(2)
Обозначим через 
и 
пространства 
и 
соответственно. Тогда задачу (2) можно записать в виде операторного уравнения
(2*)
в пространстве , где операторы 
,
определены равенствами
, 
,
где 
. Отметим, что краевая задача (2) является резонансной, так как оператор 
не обратим.
Обозначим ядро и образ линейного оператора через 
и 
соответственно. Непосредственная проверка показывает, что ядро оператора 
имеет вид:
.
Оператор является нетеровым оператором. Пространство представимо в виде: 
, где подпространство 
. Тогда элемент 
представим в виде 
, где 
и 
.
Пусть 
проектор на 
, определенный равенством 
, а 
проектор на , 
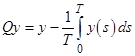. Тогда соответствующий дополнительный проектор 
имеет вид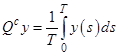 
, откуда образ оператора :
.
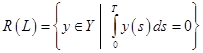Дадим определение обобщенно обратного оператора [1]: оператор 
называется обобщенно обратным к линейному оператору , ассоциированным с проектором , если справедливы равенства:
1) 
для любого 
;
2) 
для любого 
;
3) 
для любого .
Условимся в дальнейшем обобщенно обратный к оператор 
записывать просто 
.
Из нетеровости оператора следует, что существует обобщенно обратный к оператор 
, определяемый по формуле: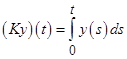 
.
Так как оператор не обратим (
), то нужно доказать существование таких множества 
и непрерывного оператора 
, что оператор 
переводит это множество в образ оператора . Для этого применяется теорема о неявном операторе к операторному уравнению:
. (3)
Замечание. Следуя [7, с. 670], будем отождествлять пространства 
и 
с согласованными нормами: 
(то есть 
, 
). Поэтому далее при необходимости прямую топологическую сумму 
будем рассматривать как прямое произведение 
с изометричной нормой, при этом значение оператора 
на элементе будем записывать в виде 
.
Рассмотрим производную оператора в некоторой точке 
как оператор вида:
,
тогда оператор 
можно представить в виде суммы операторов
,
где 
и 
.
Для решения вопроса о разрешимости уравнения (2*), а, следовательно, и задачи (1), воспользуемся теоремой из [8].
Теорема 1. Пусть оператор - нетеров, - обобщенно обратный к оператор, произведение 
вполне непрерывно, оператор непрерывен и имеет частную производную 
, непрерывную в нуле 
(в дальнейшем положим 
). Пусть далее 
, оператор 
непрерывно обратим и справедливы следующие оценки:
1) 
;
2) 
, 
;
3) 
, 
;
4) 
;
5) 
;
6) 
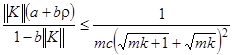, где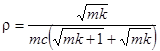 
.
Тогда существует решение уравнения .
Будем проверять условия теоремы 1 для операторного уравнения (2*) последовательно, с приведением требуемых при этом ограничений.
1. Покажем, что оператор 
является непрерывным. Поскольку функция 
, а функция 
представляет разность непрерывной функции 
и функции 
, удовлетворяющей условию Каратеодори, то оператор - непрерывен.
2. Перейдем к условию 
. Запишем уравнение (3) для операторного уравнения (2*), для этого определим вид оператора на элементе 
:
.
Откуда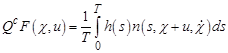 
и, следовательно, уравнение (3) запишется в виде:
.
Согласно теореме 1 должно выполняться условие , с учетом того, что условие предполагает выполнение равенства 
, получим: 
.
Тогда, поскольку условие означает, что 
, получим условие:
.
3. Далее определим вид оператора . Поскольку у оператора элемент содержит только функция 
, то
,
где 
означает частную производную функции 
по второму аргументу, действующую из в . Тогда обратный оператор для оператора 
имеет вид:
.
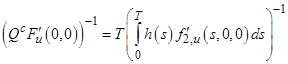Таким образом, оценка его нормы 
определяется константой:
.
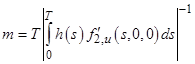4. Найдем константу 
из условия 
, в предположении, что частная производная функции по 
удовлетворяет условию Липшица по второму аргументу с константой 
: 
:
.
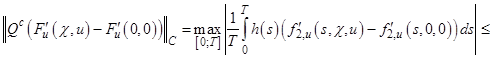
Таким образом, константа 
, где 
.
5. Далее найдем константу 
из условия , в предположении, что функция удовлетворяет условию Липшица по второму аргументу с константой 
: 
, и с учетом условия 
:
.
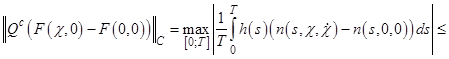
Таким образом, константа 
, где 
.
6. Найдем теперь оценку нормы 
, в предположении, что функция удовлетворяет условию: 
, и с учетом условия :
Таким образом, константы 
, где 
.
Замечание. Для доказательства полной непрерывности произведения рассмотрим распространение оператора на пространство , то есть будем считать, что оператор действует из пространства в . Тогда оператор вполне непрерывен, а, следовательно, произведение также вполне непрерывно. Нетрудно показать, что 
.
Докажем существование решения уравнения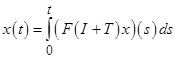 
на подпространстве 
, содержащемся в пространстве . Тогда, вследствие непрерывности оператора , правая часть данного уравнения принадлежит 
и, следовательно, само решение 
также принадлежит . Это доказывает существование решения исходной задачи (1) в пространстве .
7. Проверим выполнение условия 
. С учетом и равенства 
получим следующее условие: 
.
8. Наконец остается проверить услови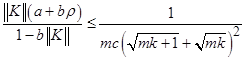е 
, где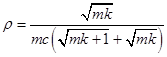 
. Для этого подставим найденные выше константы в левую часть неравенства:
.
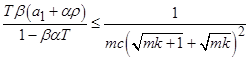Таким образом, объединяя найденные ранее оценки, получим условия разрешимости краевой задачи (1).
Теорема 2. Пусть функция 
удовлетворяет условиям Каратеодори и вместе со своей частной производной по удовлетворяют условию Липшица по второму аргументу с константами и для всех 
, то есть
,
.
Пусть далее 
непрерывна в точке , 
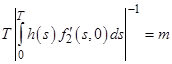, функция непрерывна и существует такая функция 
, удовлетворяющая условиям:
- для каждого фиксированного на искомом шаре с центром в точке пространства выполняется неравенство: ;
- оператор , определенный равенством: ,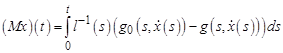
является вполне непрерывным оператором.
Тогда если функция 
и выполнены условия:
1) 
;
2) 
;
3)
4) 
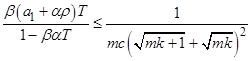, где , , , 
, , 
,
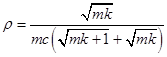то существует решение задачи (1) на шаре 
с радиусом 
.
Рецензенты:
Абдуллаев А.Р., д.ф.-м.н., профессор кафедры высшей математики Пермского национального исследовательского политехнического университета, г. Пермь.
Аристов С.Н., д.ф.-м.н., старший научный сотрудник, Институт механики сплошных сред Уральского отделения Российской академии наук, г. Пермь.