Об устойчивости квазилинейной системы дифференциальных уравнений произвольного порядка
Данная работа является непосредственным продолжением работы «Об устойчивости систем линейных дифференциальных уравнений второго, третьего и четвертого порядка» [6].
Рассмотрим произвольную квазилинейную систему дифференциальных уравнений n-го порядка, допускающую построение системы первого приближения.
Пусть система первого приближения данной системы имеет вид:
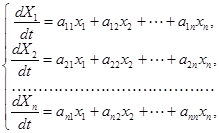(1)
где 
– постоянные действительные коэффициенты, 
– неизвестные функции параметра t. Составим соответствующее характеристическое уравнение системы (1):
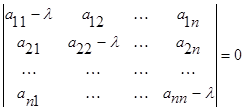. (2)
Далее, раскрывая левую часть (2), получаем уравнения в случаях четного и нечетного n:
1) для 
:
, (3)
2) для 
:
, (4)
где 
- определитель матрицы системы первого приближения (1),
…
…
– набор индексов оставляемых строк, содержащих k элементов не равных между собой;
– набор индексов оставляемых столбцов, состоящих из k элементов, не равных между собой.
Доказательства соотношений (3) и (4) получаются в результате вычисления определителей произвольного порядка методом разложения по строкам и столбцам. Отметим, что достаточным условием асимптотической устойчивости решений линейной системы дифференциальных уравнений с постоянными коэффициентами является отрицательность действительных частей всех корней характеристического уравнения [1,2,5].
Таким образом, необходимым условием устойчивости нулевого решения в рассматриваемой ситуации является отрицательность коэффициентов уравнений (3) и (4), а для получения его достаточных условий используется теорема Рауса – Гурвица [3,4]. Составим матрицу Гурвица в случаях четного и нечетного n:
1) :
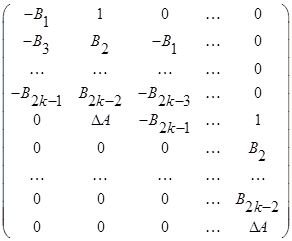; (5)
2) :
. (6)
Далее для составленных матриц (5), (6) используется критерий Рауса – Гурвица [3,4], который заключается в положительности всех миноров полученных матриц.
Пример использования критерия для квазилинейной системы дифференциальных уравнений пятого порядка
При моделировании реальных задач исследователи получают системы дифференциальных уравнений, порядок которых чаще всего не превосходит пяти. Для систем второго и третьего порядка, используя полученные теоремы [6], достаточно легко оценить устойчивость нулевого решения исходной системы. Для систем дифференциальных уравнений четвертого и пятого порядка при подсчете определителей, возможно, потребуются системы компьютерной математики.
В качестве примера подробно рассмотрим условие асимптотической устойчивости решений для систем 5-го порядка. Характеристическое уравнение (2) примет вид:
.
Уравнение (4) в данном случае примет вид:
, (7)
где 
, 
, 
, 
, причем
содержит в 
по 2 элемента, в 
по 3, в 
по 4 элемента, не равных между собой.
Необходимым условием устойчивости в рассматриваемой ситуации будет отрицательность коэффициентов уравнения (7): 
Для получения достаточных условий асимптотической устойчивости нулевого решения исходной системы составим матрицу Гурвица 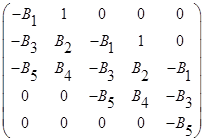(8):
(8)
и потребуем положительность всех ее диагональных миноров:
,
,
,
,
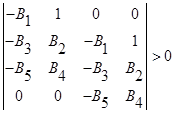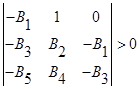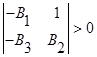. (9)
Примером неустойчивой системы дифференциальных уравнений пятого порядка является система вида (1), матрица коэффициентов которой имеет вид:
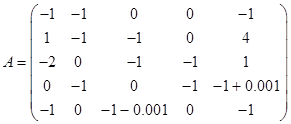. (10)
Запишем соответствующее характеристическое уравнение:
.
Несмотря на то, что необходимые условия выполняются: 
, достаточное условие нарушается. Существуют отрицательные диагональные миноры матрицы Гурвица, в частности (с точностью до тысячных):
.
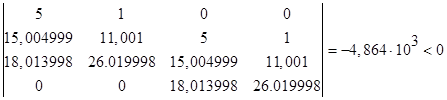Данные вычисления были произведены с помощью систем компьютерной математики MatCAD и Mathematica 6.0.
Рецензенты:
Расулов К.М., д.ф-м.н., профессор, заведующий кафедрой математического анализа Смоленского государственного университета, г. Смоленск.
Евдокимова Г.С., д.п.н., профессор, заведующий кафедрой прикладной математики Смоленского государственного университета, г. Смоленск.
Криштоп В.В., д.ф.м.н., профессор, заведующий кафедрой «Физика», Дальневосточный государственный университет путей сообщения, г. Хабаровск, профессор Университета Kwangwoon University, Korea.