Проблема лесных пожаров во всем мире остается одной из самых важных задач, стоящих как перед лесными хозяйствами, так и перед целыми государствами, лесные территории которых являются важными источниками национального дохода и объектами стратегического значения. Кроме того, каждый отдельный гражданин государства должен понимать, что его посильное участие в решении этой проблемы может иметь огромное значение, ведь подавляющее большинство пожаров, происходящих во всем мире и уничтожающих огромные лесные массивы, происходит по вине человека [2]. С ростом активности человека, растёт и количество лесных пожаров, поэтому методы тушения должны совершенствоваться. Важной составляющей борьбы с пожарами является прогнозирование их развития. В данной работе рассматриваются вопросы, связанные с влиянием рельефа местности на динамику пожара.
В основе проведённых расчётов лежит физико-математическая модель, опубликованная в [1, 3, 7], а в качестве расчётной схемы использовалась схема Харлоу [9]. Наиболее часто для моделирования химико-физических процессов используется метод Гира [5], в данной работе использовались схемы первого порядка точности, что связано, с одной стороны, с необходимостью минимизировать время расчётов, а с другой стороны, их использование гарантирует устойчивость и консервативность [7]. Кроме того, для сокращения времени вычислений использовался алгоритм оптимизации размещения данных в памяти [8]. В отличие от предыдущих работ, таких как [4], где предполагался постоянный угол наклона подстилающей поверхности, в данной работе, так же, как и в работе [6], рельеф представляется в виде ломаной.
Как показали расчёты, рельеф оказывает существенное влияние на поле скоростей, формирующееся при обтекании, поэтому перед моделированием лесного пожара необходимо решить гидродинамическую задачу.
В таблице 1 приведены оценки скорости распространения пожара на различных участках. Участок 50 - 105 м – соответствует наветренному склону для случая распространения пожара через холм и подветренному для случая распространения через овраг. Участок 105 - 145 м – соответствует распространению по равнине для всех рассматриваемых случаев. Отрезок 145 – 200 м – соответствует спуску пожара с холма и подъёму из оврага.
Таблица 1
Скорость распространения пожара на различных участках
|
Координаты отрезка, м |
Скорость пожара, при распространении через местность с холмом, м/с |
Скорость пожара, при распространении через равнину, м/с |
Скорость пожара, при распространении через местность с оврагом, м/с |
|
50-105 |
3,44 |
3,22 |
2,61 |
|
105-145 |
3,25 |
3,00 |
|
|
145-200 |
2,72 |
3,67 |
Из таблицы 1 видно, что скорость пожара на участках без наклона приблизительно одинакова, на плато холма она несколько выше вследствие эффектов обтекания. Наибольшая скорость пожара наблюдается на выходе из оврага, что связано с высоким углом наклона факела пламени.
Данные результаты боле детально показаны на рис. 1 – 3 в виде изотерм и полей скоростей для различных моментов времени: внешняя (чёрная) линия соответствует температуре – 500 К, средняя (бордовая) – 1000 К, внутренняя (красная) – 1500 К. Из результатов видно, что рельеф местности оказывает существенное влияние на скорость распространения пожара. Во всех вариантах представленных расчётов, на начальном этапе пожара наблюдается существенное увеличение ширины фронта и формирование высокой конвективной колонки.
При переходе пожара с ровной поверхности в овраг, на момент времени 10 секунд (рис. 1) с подветренной стороны фронта пожара образуется вихрь, который осуществляет подсос свежего воздуха, при этом на рис. 1 вихрь выражен слабее. На рис. 1-3 наблюдается влияние эффектов обтекание рельефа на направление основных газовых потоков, образующихся при горении. Из результатов видно, что модуль скорости над фронтом пожара при любой из рассматриваемых конфигураций рельефа существенное превышает скорость ветра в невозмущённом потоке, а отличия на начальной стадии пожара несущественны. Тем не менее, можно заметить, что на рис. 1 поток смеси газов направлен под большим углом к горизонту и на момент времени 10 секунд пожар достигает точки начала склона (рис. 1-2), при этом во всех проведённых расчётах дальность распространения пожара близка. Распространение пожара по склону показывает, что на подъёме (рис. 1) пожар продвинулся дальше уже на момент 30 секунд, чем на спуске (рис. 2) за 35 секунд. При этом распространение пожара на равнине медленнее, чем на подъёме, но быстрее, чем на спуске. При распространении пожара на холмистой местности (в момент 20 секунд) и на равнине (30 секунд) наблюдается разделение области высоких температур (выше 1500 К) на 2 части, что связано с горением летучих продуктов пиролиза впереди пожара. Распространение пожара по плато холма несколько быстрее, чем по дну оврага, что связано с изменением скорости ветра в пологе леса вследствие эффектов обтекания. На выходе из оврага пожар распространение пожара ускоряется, в результате чего средняя скорость распространения пожара через овраг и холм приблизительно одинаковы.
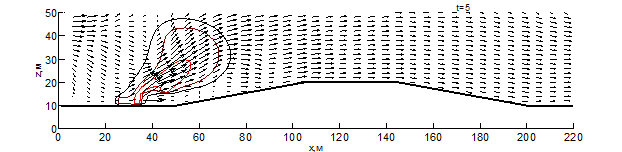
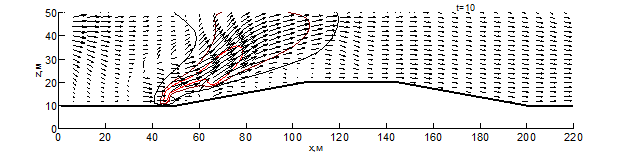
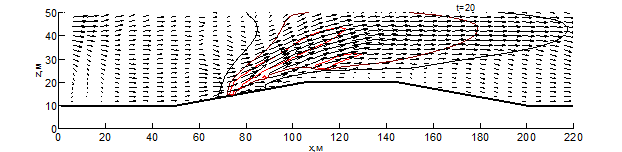
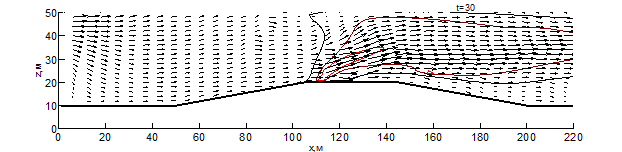
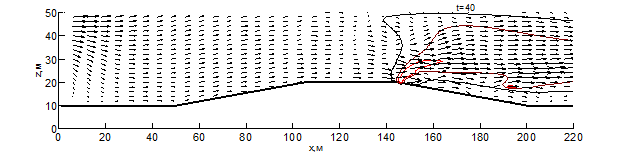
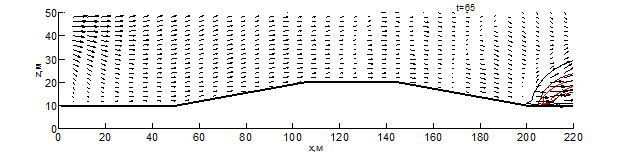
Рис. 2 – Поле скоростей и температур при распространении пожара по рельефу с трапециевидным холмом на различные моменты времени
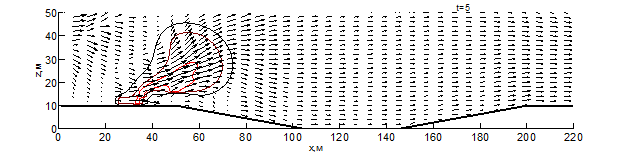
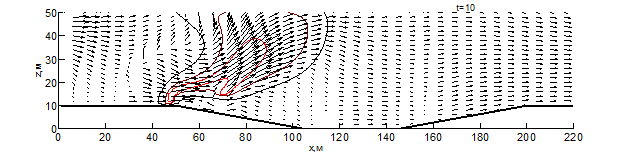
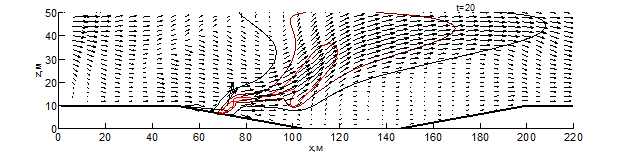
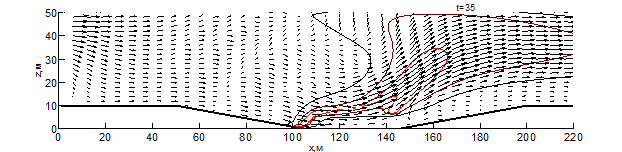
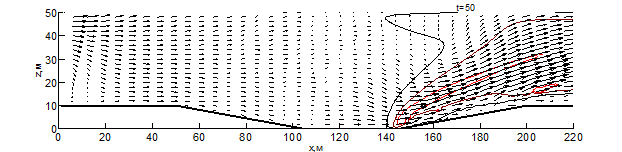
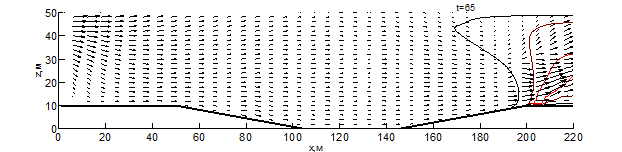
Рис. 3 – Поле скоростей и температур при распространении пожара по рельефу с трапециевидным оврагом на различные моменты времени
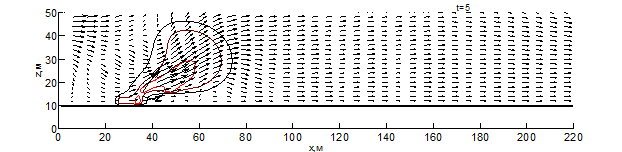
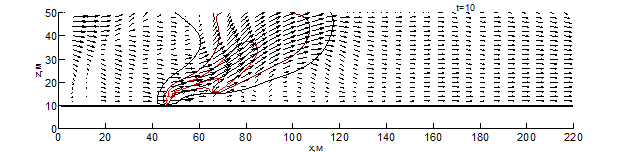
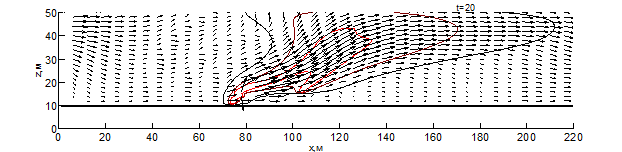
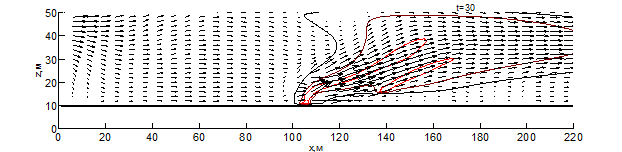
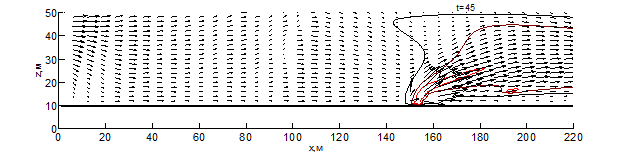
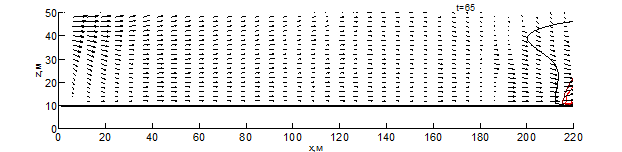
Рис. 4 – Поле скоростей и температур при распространении пожара по равнине на различные моменты времени
В данной работе показано, что скорость распространения пожара существенно зависит от неоднородностей рельефа. Ранее в работе [1] для аналогичной задачи был получен результат, показывавший более быстрое распространение пожара через холм, чем через овраг. Это различие можно объяснить меньшим углом наклона склонов (11 градусов вместо 45 в [1]), а большим размером плато холма.
Эффекты обтекания приводят к существенному изменению скорости ветра, что, в свою очередь, влияет на скорость распространения пожара. Метеорологические данные не позволяют получить данные о ветре с достаточно хорошей разрешающей способностью для учёта вклада неоднородностей рельефа малого размера. Именно поэтому при моделировании лесных пожаров целесообразно учитывать эффекты обтекания ландшафта.
Работа выполнена при финансовой поддержке 13-03-91164-ГФЕН_а «Экспериментальное исследование кинетики и механизма термического разложения лесных горючих материалов и процессов распространения пламени по их слою».
Рецензенты:
Петрухин Н.С., д.ф.-м.н., ординарный профессор Национального исследовательского университета «Высшая школа экономики», г. Нижний Новгород.
Карпухин В.Б., д.ф.-м.н., профессор кафедры «Высшая и прикладная математика», Российской открытой академии транспорта Московского государственного университета путей сообщения, г. Москва.



