Введение. Для уменьшения затрат на ревизию трансформаторов предлагается исследовать обмотки трансформаторов при подключении импульсного напряжения [1, 2, 5]. Длина импульса – теста составляет 400-500 нс.
Цель исследования создать математическую модель трансформатора. Модель можно использовать для моделирования дефектов обмоток, формировать эталонные сигналы при различных повреждениях исследуемого оборудования.
Вывод основных соотношений
При диагностике трансформатора импульсом короткой длительности, необходимо учитывать два обстоятельства. Первое: обмотке трансформатора следует сопоставлять электротехническую схему замещения с распределенными параметрами. Второе: из-за короткой длительности зондирующего импульса необходимо учитывать скин-эффект [4], зависимость параметров схемы замещения от частоты. При рассмотрении двухобмоточного трансформатора схему замещения нужно представлять для каждой обмотки в отдельности. Приведем этапы формирования моделей обмоток трехфазного двухобмоточного трансформатора, приведенного на рисунке 1. На рисунке 1 приведены формы внутренней (низковольтной) и внешней (высоковольтной) обмоток трансформатора и поперечные сечения проводов обмоток соответственно.
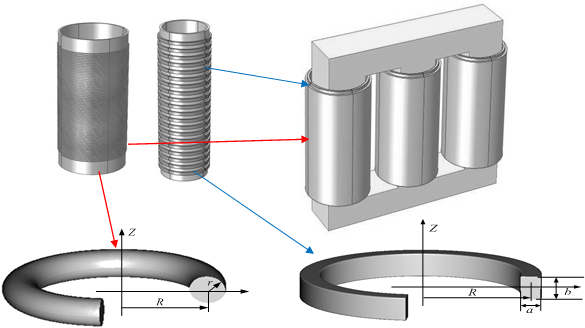
Рис. 1. Обмотки трехфазного двухобмоточного трансформатора и поперечные сечения проводов обмоток, а – внутренняя обмотка трансформатора (НН); б – внешняя обмотка трансформатора (ВН); в – трехфазный трансформатор; г – поперечное сечение провода обмоток соответственно.
1. Электротехническая схема замещения одного витка обмотки
Виток обмотки заменяется электротехническим звеном, состоящим из элементов, приведенных на рисунке 2, а. Здесь 
– межвитковая емкость, 
– емкость между витком и заземленными частями трансформатора, 
– индуктивность рассеяния обмотки с учетом взаимной индуктивности между соседними элементами обмотки, 
– активное сопротивление витка соответственно.
а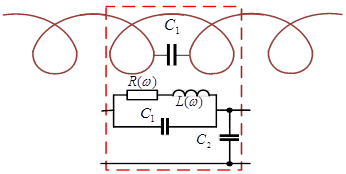 
б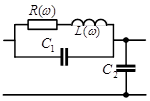 
Рис. 2. Электротехническая схема замещения: а – одного витка обмотки трансформатора; б – схема замещения обмотки трансформатора
Все приведенные величины являются погонными, т.е. значения величин отнесены к единице длины. Таким образом, обмотку трансформатора можно заменить последовательно соединенными звеньями (рисунок 2, б).
Относительный вклад высокочастотных компонент в формирование спектра зондирующего импульса короткой длительности достаточно высок. При дальнейшем укорачивании импульса относительный вклад высокочастотных компонент усиливается. Как следствие этого явления, при очень коротких длительностях зондирующего импульса начинает проявляться скин-эффект [3, 4]. То есть, при высокочастотном токе в поперечном сечении проводника, ток выталкивается из внутренней области к периферии проводника. При этом начинает проявляться зависимость индуктивности и сопротивления проводника от частоты.
Для определения величин электротехнических элементов, входящих в схему замещения, определим частотный спектр и частотный диапазон зондирующего импульса, а затем приведем расчет индуктивности и сопротивления витков обмотки трансформатора круглого и прямоугольного сечения.
2. Частотное разложение зондирующего импульса.
В качестве модельного зондирующего импульса выберем функцию с длительностью 
мкс в виде:
а 
б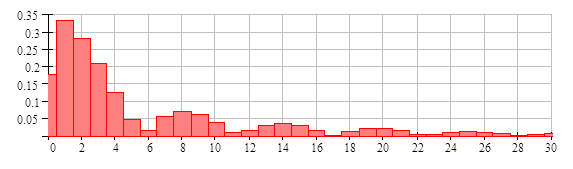 
в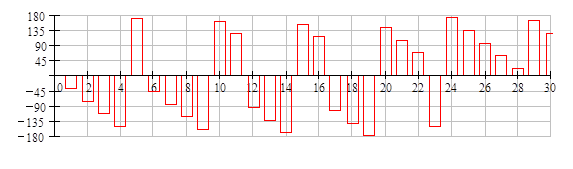 
Рис. 3. Зондирующий импульс (t в мкс): а – исходный импульс показан сплошной линией, пунктирной показан зондирующий импульс, полученный в среде MathCAD (t в мкс)); б - амплитудно-частотный спектр; в – фазо-частотный спектр
Определим частотный спектр импульса. Для этого разложим импульс в ряд Фурье, определив коэффициенты разложения 
. Для определения коэффициентов использовалась стандартная программа быстрого преобразования Фурье (FFT) программно-интегрированной среды MathCAD. Далее функция представлялась в виде ряда:
где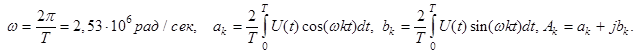 
Спектр и результат восстановления функции по коэффициентам представлены ниже.
Число коэффициентов разложения бралось N=30. Из спектра импульса видно, что начиная с 10 гармоники, относительный вклад высших гармоник в импульсе не превышает 5%.
3. Расчет индуктивности и сопротивления витков круглого и прямоугольного поперечного сечения с учетом скин-эффекта.
Проведем расчет плотности распределения тока в поперечном сечении проводника. Система уравнений Максвелла [3, 4] позволяют получить уравнение для векторного потенциала 
, позволяющего определить плотность распределения тока по сечению проводника:
, (1)
где – векторный магнитный потенциал, 
– напряжения проводника, 
диэлектрическая проницаемость, 
– частота, 
– магнитная проницаемость, 
– проводимость, 
мнимая единица.
Плотность тока и ток определяются выражениями [3]:
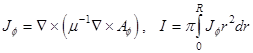. (2)
Магнитная энергия определяется выражением [4]:
, (3)
из которого при известном токе определяется индуктивность с помощью соотношения [3]:
(4)
При известном напряжении и токе определяем сопротивление проводника, используя формулу:
(5)
Для расчета представленных уравнений использовался математический пакет COMSOL Multihpysics, основанный на методе конечных элементов (Finite Element Method (FEM)). Результаты расчетов приведены на рисунках 4, 5.
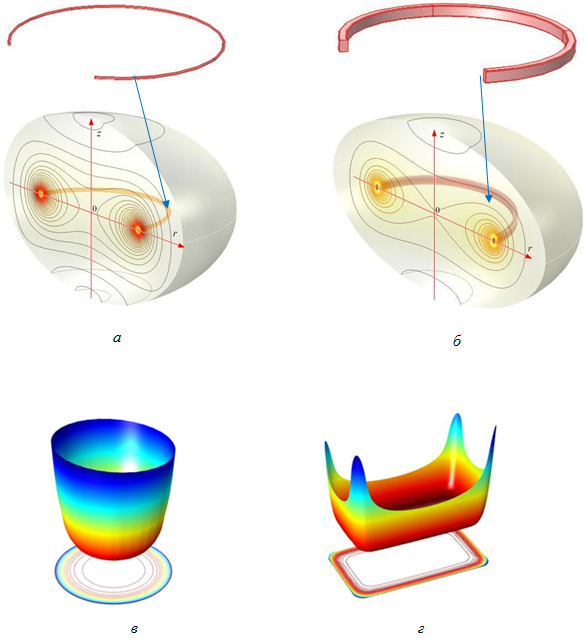
Рис. 4. Поле распределения магнитного потенциала кольцевых проводников: а – круглого и б – прямоугольного сечения при фиксированной частоте.
Распределение плотности тока в поперечном сечении проводника при частоте 
Гц, в – круглого; г – прямоугольного соответственно
а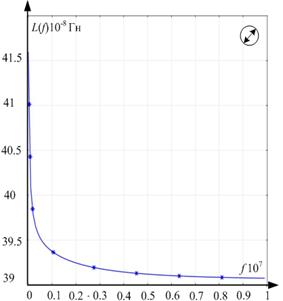 
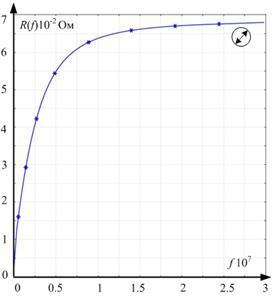
б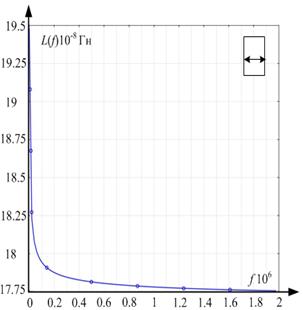 
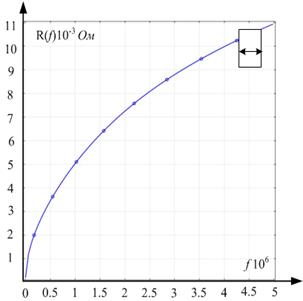
Рис. 5. Частотные зависимости индуктивности L(f) и сопротивления R(f) провода: а – с круглым поперечным сечением; б – с прямоугольным поперечным сечением
При известных зависимостях индуктивности и сопротивления от частоты можно определить переходные процессы, происходящие в обмотках трансформатора. Поскольку входной импульс представлен в виде суммы гармоник, расчет проводился с использованием метода наложения. То есть рассчитывались напряжения и токи для каждой гармоники. Затем результаты расчетов токов и напряжений каждой гармоники складывались и получались результирующие токи и напряжения при воздействии зондирующего импульса.
Запишем уравнение дифференциальные уравнения для определения напряжения и токов в реактивных элементах схемы замещения (рисунок 6) для одного витка с учетом внутреннего сопротивления источника r. Для решения дифференциальных уравнений использовался метод пространства состояний, дифференциальное уравнение третьего порядка представлялось в виде системы 3-х уравнений первого порядка. Уравнения рассчитывались численно с использованием метода Рунге-Кутта четвертого порядка с фиксированным шагом. Число точек дискретизаций равнялось N=103 .
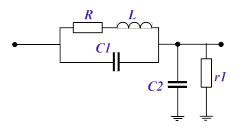
Рис. 6. Электротехническая схема замещения одного витка обмотки трансформатора
а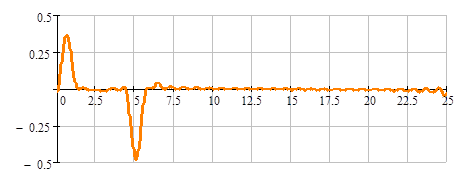 
б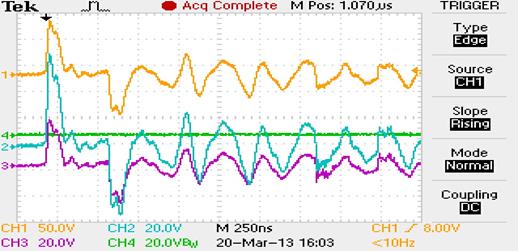 
Рис.7. Напряжение на конденсаторе 
: а – в результате моделирования; б – экспериментальные осциллограммы напряжений на витке при зондировании пробным импульсом
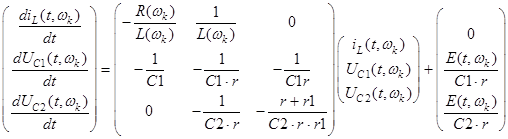
Здесь 
– гармоническая составляющая входного импульса при фиксированной частоте, 
– ток индуктивности, 
– напряжение на первом и втором конденсаторах. Результирующие токи и напряжения представляются в виде ряда:
рад/сек.
Результаты расчетов для провода круглого сечения приведены на рисунке 7, а.
График напряжения на конденсаторе С1, рассчитанный теоретически, удовлетворительно совпадает с экспериментом. Что свидетельствует об адекватности модели.
Для провода с прямоугольным поперечным сечением графические зависимости выглядят аналогично.
Выводы
Полученная математическая модель позволяет определить токи и напряжения с достоверной погрешностью для дальнейших исследований без использования натурного эксперимента. Форма напряжения на катушке, полученная на построенной модели полностью совпала с экспериментальной осциллограммой, следовательно модель можно использовать для моделирования дефектов обмоток, формировать эталонные сигналы при различных повреждениях исследуемого оборудования.
Рецензенты:
Усов Ю.П., д.т.н., профессор кафедры ЭСиЭ ЭНИН ФГБОУ ВПО «НИ ТПУ», Национальный исследовательский Томский политехнический университет, г. Томск.
Сивков А.А., д.т.н., профессор кафедры ЭПП ЭНИН ФГБОУ ВПО «НИ ТПУ», Национальный исследовательский Томский политехнический университет, г. Томск.