Scientific journal

Modern problems of science and education

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

При разработке различных специализированных вычислителей на ПЛИС часто встает вопрос нахождения значения некоторой показательной функции вида . К таким функциям относятся , , и им подобные. Обычно для получения численного значения этих функций используют известные разложения в степенные ряды. Однако такой подход не является универсальным, так как требует создания для вычисления каждой из них собственного алгоритма, адаптированного для ПЛИС. Здесь, в зависимости от конкретных технических требований к разработке, могут применяться, либо широко известная схема Горнера [2], либо более универсальные схемы с предварительной обработкой коэффициентов [4], либо алгоритмы, построенные на основе графа, представленного в параллельной канонической форме, либо табличный метод.

Последний из перечисленных табличный метод является наиболее универсальным, однако при повышении точности вычисления он требует значительных аппаратных ресурсов, используемых для хранения исходных таблиц. Так при абсолютной погрешности вычисления функции в диапазоне порядка 2.3Е-10, что соответствует 32 точным разрядам результата, требуется хранить не менее табличных значений функции. Этот недостаток может быть частично компенсирован за счет использования дополнительной обработки табличных данных, например, методом линейной интерполяции [3]. Однако и в этом случае сохраняется необходимость в хранении значительных объемов информации.

Используя одно из основных свойств показательной функции, а именно – соотношение:

, (1)

можно предложить универсальный алгоритм вычисления, обеспечивающий высокое быстродействие при малых аппаратных затратах на реализацию.

Рассмотрим данный подход на примере вычисления экспоненциальной функции. Предположим, что диапазон изменения аргумента равен и его разрядность составляет 16 бит. Требуемое число верных разрядов результата – 32.

Представим аргумент в виде:

,

где ; , и т.д. – соответствующие разряды ; – целые числа, составленные из соответствующих разрядов .

Тогда, используя (1), для рассматриваемой функции можно записать:

.

Таким образом, процесс вычисления функции разбивается на несколько параллельных процессов. В нашем случае процессов 8, причем в каждом из них, так как используется два разряда аргумента, вычисляются только 4 значения функции, одно из которых нулевое. Применим к каждому процессу табличный метод. В результате для вычисления функции необходимо хранить только 32 табличные значения.

На рис. 1 приведен соответствующий данному случаю граф алгоритма вычисления.

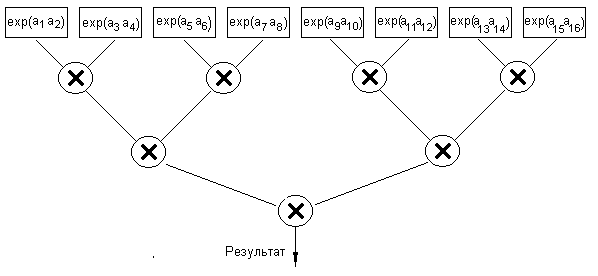
Рис. 1. Алгоритм вычисления при разрядности аргумента – 16 бит

Реализация данного алгоритма требует 3-х ярусов умножения, то есть суммарное время вычисления будет равно:

, (2)

где – время чтения табличного значения функции, – время выполнения операции умножения, – количество последовательно выполняемых операций умножения.

Анализируя граф на рис. 1, нетрудно получить общую формулу для вычисления значения :

, (3)

где – число разрядов аргумента .

Для определения разрядности табличных значений функции воспользуемся известным правилом, согласно которому при перемножении двух приближенных чисел их относительные погрешности складываются. Тогда, используя полученную, согласно [1], связь между относительной ошибкой и числом верных разрядов приближенного числа (, где – число разрядов дробной части числа), для числа верных разрядов произведения двух чисел можно записать:

,

где и – минимальная разрядность дробной части и разность разрядностей сомножителей соответственно.

Если разрядности сомножителей одинаковы, то, согласно приведенному соотношению, число верных разрядов результата будет на единицу меньше, чем у сомножителей.

Возвращаясь к графу на рис. 1, можно сказать, что разрядности табличных значений должны быть, как минимум, на 3 разряда больше разрядности результата. В нашем случае табличные значения должны содержать не менее 35 верных разрядов. В тестируемом ниже варианте программы число верных разрядов табличных данных было принято равным 36.

На рис. 2 приведены временные диаграммы моделирования рассмотренного алгоритма в среде САПР Quartus II фирмы Альтера [5], а в таблице – расшифровка полученных результатов.

Рис. 2. Временные диаграммы моделирования рассмотренного алгоритма

Таблица. Результаты тестирования проекта

При реализации проекта на ПЛИС серии Stratix III потребовалось 27 комбинационных таблиц (ALUTs) и 28 18-битных DSP блоков. Максимальное время вычисления не превосходит 27 nS. Анализ результатов тестирования показал, что во всем диапазоне изменения аргументов получено не менее 33 верных разрядов результата, что подтверждает правильность выбора точности табличных значений функции.

Следует отметить, что увеличение разрядности аргумента, согласно выражениям (2) и (3), не сильно скажется на времени вычисления. Так, при разрядности аргумента не более 32 в графе на рис. 1 появится еще только один дополнительный ярус умножения, то есть время вычисления увеличится на время . Значительно изменится ширина графа, то есть количество одновременно выполняемых операций.

Согласно данным из User Guide для мегафункции altpf_exp фирмы Альтера, вычисление функции при числе верных разрядов результата 23 требует: комбинационных блоков (ALUTs) – 631 шт, специализированных регистров (DLRs) – 521 шт, модулей ALMs – 445 шт, 18-ти разрядных DSP блоков – 19 шт. Общее время вычисления для ПЛИС той же серии составляет 62 nS. Следует отметить, что мегафункция altpf_exp работает с данными, представленными, согласно стандартам IEEE 754, что делает ее более универсальной. Однако при ограниченном диапазоне изменения аргумента рассмотренный алгоритм обладает явным преимуществом как по затратам аппаратных ресурсов ПЛИС, так и по быстродействию.

Рецензенты:

Волков Н.Н., д.т.н., профессор Московского государственного технического университета им. Н. Э. Баумана (МГТУ им. Н. Э. Баумана), кафедра «Информационные системы и телекоммуникации», г.Москва.

Шевцов Д.А., д.т.н., профессор Московского авиационного института (национального исследовательского университета), кафедра № 306 «Микроэлектронные электросистемы», г.Москва.