Заметим, что такую динамическую систему можно создавать как с точки зрения объектно-ориентированного программирования, так и функционального [2]. Заметим также, что для полного анализа проекта неизбежно потребуется пользоваться фундаментальными математическими знаниями. Поэтому для программирования указанной выше системы управления проектом удобно использовать системы компьютерной алгебры, например Mathematica или MATLAB. А предложенный функционально-матричный метод в этих системах прост для программирования.
Цель исследования: обеспечение выборочного (по запросу пользователя) вычисления параметров работы сетевого графа любого этапа проекта (вершины – работы) без непосредственного последовательного расчета, как это делается в известном табличном методе.
Объекты исследования: сетевые графы (вершины работы) проекта.
Алгоритм
Пусть некоторый
проект состоит из ![]() периодов. Ниже введем
в рассмотрение следующие функции:
периодов. Ниже введем
в рассмотрение следующие функции: ![]() – время, начиная
с которого приступили к выполнению
– время, начиная
с которого приступили к выполнению ![]() -го периода;
-го периода; ![]() – количество работ в
– количество работ в ![]() -м периоде;
-м периоде; ![]() –
время выполнения
–
время выполнения ![]() -й работы
-й работы ![]() -го периода (
-го периода (![]() ).
).
Будем считать,
что работы каждого этапа проекта имеют правильную нумерацию. Пусть для каждого
фиксированного периода ![]() – матрица предшествующих
работ. Каждая компонента
– матрица предшествующих
работ. Каждая компонента ![]() этой
матрицы, т.о., является функцией от номера периода. Будем считать, что
этой
матрицы, т.о., является функцией от номера периода. Будем считать, что ![]() это номер строки,
это номер строки, ![]() - номер столбца, строки матрицы
предшествующих работ – «работы-потомки», а столбцы – работы, непосредственно
предшествующие «работам-потомкам». На позицию
- номер столбца, строки матрицы
предшествующих работ – «работы-потомки», а столбцы – работы, непосредственно
предшествующие «работам-потомкам». На позицию ![]() в
этой матрице ставится 1, если
в
этой матрице ставится 1, если ![]() -я работа
непосредственно предшествует
-я работа
непосредственно предшествует ![]() -й работе, и
0, если
-й работе, и
0, если ![]() -я работа непосредственно не
предшествует
-я работа непосредственно не
предшествует ![]() -й работе. Обратим внимание на
то, что матрицу
-й работе. Обратим внимание на
то, что матрицу ![]() мы рассматриваем не
как массив, а как функцию от
мы рассматриваем не
как массив, а как функцию от ![]() .
Такой подход упрощает написание кода (например, в Mathematica) для
нахождения параметров работ.
.
Такой подход упрощает написание кода (например, в Mathematica) для
нахождения параметров работ.
Заметим, что матрица
смежности для графа ![]() -го периода есть
транспонированная матрица предшествующих работ (
-го периода есть
транспонированная матрица предшествующих работ (![]() ).
).
Алгоритм функционально-матричного метода расчета параметров
для работ ![]() -го периода
-го периода
1. Нахождение матрицы ранних сроков начала и окончания работ.
Обозначим через ![]() - матрицу-функцию ранних сроков начала и
окончания
- матрицу-функцию ранних сроков начала и
окончания ![]() -й работы
-й работы ![]() -го периода. Первая компонента этого списка
– номер работы
-го периода. Первая компонента этого списка
– номер работы ![]() -го периода, вторая
-го периода, вторая ![]() –
ранний срок начала этой работы, третья
–
ранний срок начала этой работы, третья ![]() –
ранний срок окончания этой работы.
–
ранний срок окончания этой работы.
Матрица-функция ранних сроков начала и окончания
![]() -й работы
-й работы ![]() -го
периода находится следующим образом. Всегда первая компонента этой матрицы-функции
– номер работы
-го
периода находится следующим образом. Всегда первая компонента этой матрицы-функции
– номер работы ![]() -го периода, третья
компонента (ранний срок окончания этой работы) получается прибавлением времени
выполнения этой работы к уже вычисленной второй компоненте (началу выполнения
этого периода). А вторая компонента формируется следующим образом.
-го периода, третья
компонента (ранний срок окончания этой работы) получается прибавлением времени
выполнения этой работы к уже вычисленной второй компоненте (началу выполнения
этого периода). А вторая компонента формируется следующим образом.
- Если ![]() -строка
матрицы предшествующих работ нулевая, то вторая компонента (раннее начало
-строка
матрицы предшествующих работ нулевая, то вторая компонента (раннее начало ![]() -й работы
-й работы ![]() -го
периода) равна времени начала выполнения этого периода
-го
периода) равна времени начала выполнения этого периода ![]() .
.
- Если ![]() -строка
матрицы предшествующих работ ненулевая, то вторая компонента (раннее начало
-строка
матрицы предшествующих работ ненулевая, то вторая компонента (раннее начало ![]() -й работы
-й работы ![]() -го
периода) находится так: берутся
-го
периода) находится так: берутся ![]() первых
элементов
первых
элементов ![]() -й строки матрицы
предшествующих работ этого периода, накладываются на одномерную матрицу для
этого периода, состоящую из значений третьих компонент матрицы
-й строки матрицы
предшествующих работ этого периода, накладываются на одномерную матрицу для
этого периода, состоящую из значений третьих компонент матрицы ![]() (
(![]() ).
Совпадающие
элементы перемножаются. Получаются
).
Совпадающие
элементы перемножаются. Получаются ![]() чисел. Из
этих чисел выбирается максимальное. Это число и есть вторая компонента
одномерной матрицы
чисел. Из
этих чисел выбирается максимальное. Это число и есть вторая компонента
одномерной матрицы
![]() для данного периода (раннее начало
для данного периода (раннее начало ![]()
![]() -й
работы
-й
работы ![]() -го периода) в этом случае.
-го периода) в этом случае.
Только что предложенный алгоритм нахождения матрицы ранних сроков начала и окончания работ запишем формулами:
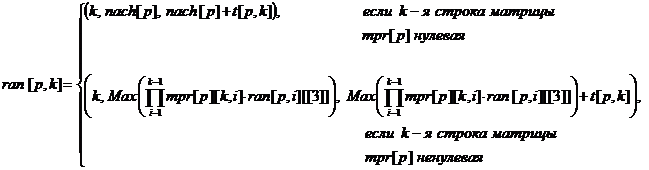 Например,
код в системе Mathematica 10,
реализующий вычисление ранних сроков начала и окончания работ, согласно
предложенному здесь функционально-матричному методу можно записать так:
Например,
код в системе Mathematica 10,
реализующий вычисление ранних сроков начала и окончания работ, согласно
предложенному здесь функционально-матричному методу можно записать так:

2. Нахождение длины критического пути.
Напомним, что критический путь это
максимальный по продолжительности полный путь. Поэтому длина критического пути ![]() для
сетевого графа
для
сетевого графа ![]() -го периода (т.е.
самый ранний момент времени, к которому завершится выполнение всех работ этого
периода) равна максимуму из ранних сроков окончания работ этого периода.
Запишем это формулами:
-го периода (т.е.
самый ранний момент времени, к которому завершится выполнение всех работ этого
периода) равна максимуму из ранних сроков окончания работ этого периода.
Запишем это формулами:
![]() .
.
3. Нахождение матрицы поздних сроков начала и окончания работ.
Обозначим через ![]() - матрицу-функцию поздних сроков начала
и окончания
- матрицу-функцию поздних сроков начала
и окончания ![]() -й работы
-й работы ![]() -го периода. Первая компонента этого
списка – номер работы
-го периода. Первая компонента этого
списка – номер работы ![]() -го периода, вторая
-го периода, вторая ![]() –
поздний срок начала этой работы, третья
–
поздний срок начала этой работы, третья ![]() –
поздний срок окончания этой работы.
–
поздний срок окончания этой работы.
Матрица-функция поздних сроков начала и
окончания ![]() -й работы
-й работы ![]() -го периода находится следующим образом.
Всегда первая компонента этой матрицы-функции – номер работы
-го периода находится следующим образом.
Всегда первая компонента этой матрицы-функции – номер работы ![]() -го периода, вторая компонента (поздний
срок начала этой работы) получается вычитанием времени выполнения этой работы от
третьей компоненты (позднего окончания выполнения работы этого периода). А третья
компонента формируется следующим образом.
-го периода, вторая компонента (поздний
срок начала этой работы) получается вычитанием времени выполнения этой работы от
третьей компоненты (позднего окончания выполнения работы этого периода). А третья
компонента формируется следующим образом.
- Если ![]() -столбец
матрицы предшествующих работ нулевой, то третья компонента
-столбец
матрицы предшествующих работ нулевой, то третья компонента ![]() (позднее
окончание
(позднее
окончание ![]() -й работы
-й работы ![]() -го периода) равна длине критического
пути этого периода.
-го периода) равна длине критического
пути этого периода.
- Если ![]() -столбец
матрицы предшествующих работ ненулевой, то третья компонента
-столбец
матрицы предшествующих работ ненулевой, то третья компонента ![]() (позднее
окончание
(позднее
окончание ![]() -й работы
-й работы ![]() -го периода) ищется так: сначала от столбца,
состоящего из поздних сроков окончания всех непосредственно следующих за
-го периода) ищется так: сначала от столбца,
состоящего из поздних сроков окончания всех непосредственно следующих за ![]() -й работой
-й работой ![]() -го
периода работ, отнимается длительность (время выполнения) этих работ; затем из
получившегося столбца выбирается наименьший элемент; этот элемент и есть третья
компонента
-го
периода работ, отнимается длительность (время выполнения) этих работ; затем из
получившегося столбца выбирается наименьший элемент; этот элемент и есть третья
компонента ![]() (позднее окончание
(позднее окончание ![]() -й работы
-й работы ![]() -го
периода) одномерной матрицы
-го
периода) одномерной матрицы ![]() в
этом случае.
в
этом случае.
Заметим, что столбец,
состоящий из поздних сроков окончания всех непосредственно следующих за ![]() -й работой
-й работой ![]() -го
периода работ, получается покомпонентным произведением столбца, состоящего из
-го
периода работ, получается покомпонентным произведением столбца, состоящего из ![]() последних элементов
последних элементов ![]() -го столбца матрицы предшествующих работ на
столбец, состоящий из поздних сроков окончания для всех работ, начиная с
-го столбца матрицы предшествующих работ на
столбец, состоящий из поздних сроков окончания для всех работ, начиная с ![]() -й работы
-й работы ![]() -го
периода.
-го
периода.
Только что предложенный алгоритм нахождения матрицы поздних сроков начала и окончания работ запишем формулами:

Здесь
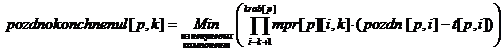 .
.
Например, код в системе Mathematica 10, реализующий вычисление поздних сроков начала и окончания работ, согласно предложенному здесь функционально-матричному методу можно записать так:

4. Нахождение матрицы полного резерва времени выполнения работ.
Напомним, что полный резерв времени
выполнения работы это максимально возможный запас времени, на который можно
отсрочить начало этой работы или увеличить продолжительность её выполнения при
условии, что завершение этой работы наступит не позднее своего позднего срока.
Поэтому очевидно, что полный резерв времени ![]() выполнения
выполнения
![]() -й работы
-й работы ![]() -го
периода равен разности поздних и ранних сроков окончания (или начала) этой
работы, т.е. вычисляется по формуле [1; 5]:
-го
периода равен разности поздних и ранних сроков окончания (или начала) этой
работы, т.е. вычисляется по формуле [1; 5]:
![]()
Примеры
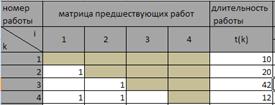
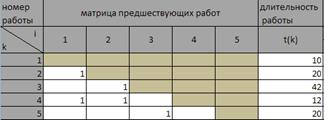
Пусть проект состоит из двух периодов, в первом периоде четыре работы, во втором – пять. Пусть для каждого из периодов заданы матрицы предшествующих работ и длительности этих работ (рис. 1). Здесь пустая клетка означает нулевое значение.
|
1 период
|
2 период
|
Рис. 1. Матрицы предшествующих работ периодов проекта.
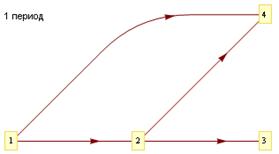
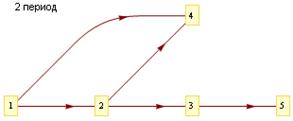
Заметим, что сетевые графики этих периодов работ соответственно будут иметь вид, приведённый на рис. 2.
|
|
|
Рис. 2. Сетевые графики выполнения периодов проекта
Параметры работ, вычисленные в системе компьютерной алгебры Mathematica по указанному выше алгоритму, приведены на рис. 3.
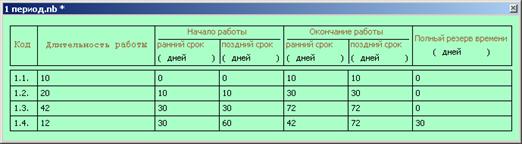
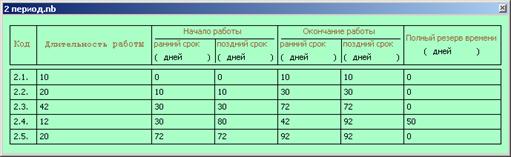
Рис. 3. Расчет параметров для сетевых графиков выполнения периодов проекта
Заключение
В настоящей работе предложен новый метод вычисления параметров сетевого графа, в котором вершинами являются работы. Он основан одновременно и на матричном подходе, и на функциональном. Прост для программирования. Этот метод обеспечивает выборочное (по запросу пользователя) вычисление параметров работы сетевого графа любого этапа проекта (вершины – работы) без непосредственного последовательного расчета, как это делается в известном табличном методе.
Предложенный здесь метод может быть использован в научных исследованиях, а также в учебном процессе при изучении дисциплин «Дискретная математика», «Системы компьютерной алгебры в управлении проектами», «Календарное планирование», «Сетевое планирование и управление».
Рецензенты:Зарипов Р.Г., д.ф.-м.н., профессор, зам. директора по научной работе, ИММ КазНЦ РАН, г. Казань;
Уткина Е.А., д.ф.-м.н., доцент кафедры информационных систем, ФГАОУ ВПО «Казанский (Приволжский) федеральный университет», г. Казань.
Библиографическая ссылка
Шустова Е.П. ФУНКЦИОНАЛЬНО-МАТРИЧНЫЙ МЕТОД РАСЧЕТА ПАРАМЕТРОВ СЕТЕВОГО ГРАФА (ВЕРШИНЫ – РАБОТЫ) // Современные проблемы науки и образования. 2015. № 1-2. ;URL: https://science-education.ru/ru/article/view?id=19874 (дата обращения: 16.12.2025).