Приближенное уравнение можно рассматривать как некоторое уравнение (основное) с точными числами (роль которых играют основные числа соответствующих приближенных чисел) при наличии некоторой дополнительной информации о степени неопределенности самого уравнения (его решений; сводится к заданию абсолютных погрешностей приближенных чисел).
Решается основное уравнение; участвующие в его записи числа в процессе решения считаются точными. Погрешности же этих чисел учитываются только для определения погрешности корня и максимальной погрешности округления, допустимой в процессе вычислений.
Участвующие в записи уравнения приближенные числа варьируются в пределах их погрешностей. Тогда каждый из корней уравнения (с изменяющимися параметрами) описывает некоторое замкнутое множество. Модуль разности между переменным корнем, описывающим это множество, и корнем основного уравнения будет изменяться от нуля (когда переменное уравнение совпадет с основным) до некоторого наибольшего значения. Это наибольшее значение модуля разности даст безусловную погрешность. Абсолютная величина разности (между найденным и ближайшим к нему точным решениями основного уравнения) определяют условную погрешность (зависит от вычислителя: он при желании может сделать ее как угодно малой). Сумма безусловной и условной погрешностей корня даст полную погрешность корня.
Если заданное приближение уравнения имеет вид
то основное уравнение имеет вид
- неизвестное; 
- заданные приближенные числа.
В окрестности каждого однократного корня x0 определяет x как неявную функцию от 
. Справедливо
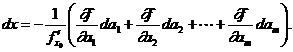
Если погрешности 
достаточно малы, то это соотношение можно использовать для определения безусловной погрешности корня x0:
В частности, для алгебраического уравнения
получаем:
Если все коэффициенты заданы с одинаковой абсолютной погрешностью e, то
.
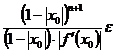Как уже отмечалось, решение приближенного уравнения сводится к приближенному решению основного уравнения. После того как ориентировочно найдена величина одного из корней, вычисляется безусловная погрешность этого корня. Ориентируясь на требуемую величину условной погрешности результата, можно определить точность, с которой следует вести вычисления. Потерей точности будет отношение условной абсолютной погрешности к абсолютной погрешности округления, если вычисления ведутся с одинаковым порядком последней значащей цифры, и отношение соответствующих относительных погрешностей, если вычисления ведутся с постоянным числом значащих цифр. После определения корня для контроля вычисляется условная погрешность (до бесконечно малых второго порядка для однократного корня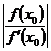
).
Отметим, определение условной погрешности корня x0 , не превосходящей его безусловной погрешности, может быть произведена и без вычисления самих погрешностей по формуле
В частности, для алгебраического уравнения, коэффициенты которого заданы с одинаковой погрешностью e, справедливо
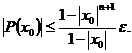
Например, для квадратного уравнения
или
(приближенное деление коэффициентов уравнения на 1,274) получим
.
Безусловные погрешности корней:
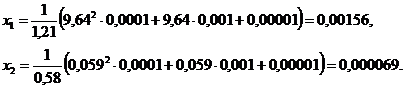
Чтобы условная погрешность не превосходила безусловной, x1 следует вычислить с точностью до тысячных, а x2 – до стотысячных;
.
Так как здесь определяются одновременно оба корня, то вычисления следует вести с таким расчетом, чтобы результат получился с пятью верными знаками после запятой. С этой целью добавляются дополнительные значащие цифры 00 в числе 12,362 и цифра 0 – в числе 1,2741. Потеря точности в данном случае невелика (так как производятся всего четыре округления), так что в промежуточных операциях достаточно сохранить пять десятичных знаков:
Отметим, что вычисления, произведенные без запасных значащих цифр, дали бы неверное значение 
. Это подтверждает правильность сделанного ранее замечания о том, что погрешности заданных чисел следует учитывать лишь при определении безусловной погрешности корня. После этого при решении уравнения заданные числа нужно считать точными (то есть решить основное уравнение). Погрешностями участвующих в вычислениях чисел считаются только погрешности округления.
Для иллюстрации рассмотрим декомпозицию динамической системы [3; 5-7], характеристики которого приняты в соответствии с таблицей 2.1 [10] для случая М=0,9; H=12 км.
Продольное движение. Характеристический многочлен системы имеет вид
.
Заменой переменной 
получим многочлен
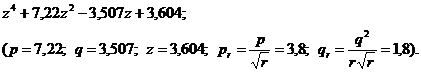
Действительных корней у многочлена нет. В соответствии с [10] при приближенных вычислениях 
воспользуемся таблицей значений функций
|
|
|
|
|
0 0,2 0,3 0,27 |
- 5,2 3,63 3,97 |
3,8 3,88 4,01 3,95 |
Таким образом, без построения графиков 
и 
с точностью до 0,002 можно принять
;
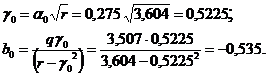
Откуда
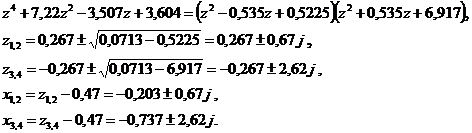
Боковое движение. Вычислив коэффициенты характеристического многочлена по таблице 2.2 [10], получим
или
.
Построив графики функций 
, убеждаемся, что все корни многочлена действительные (рис. 1).
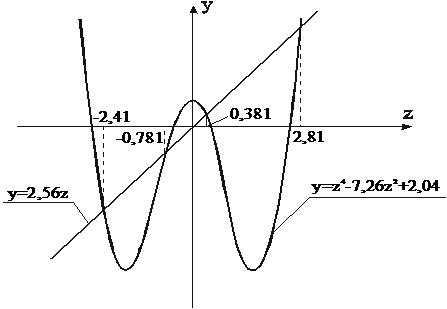
Рис. 1. К декомпозиции бокового движения.
Соответственно
В уравнении
имеем:
Пользуясь таблицей значений 
и 
, находим решение уравнения 
, соответственно 
, 
.
Декомпозиция полинома представится в виде
С точностью до 10-2 получатся те же корни 
и соответственно 
.
Рассмотренный подход успешно использовался и при идентификации параметров кинетических процессов формирования физико-механических характеристик полидисперсных материалов [2; 4; 8; 9].
Рецензенты:
Кошев А.Н., д.т.н., профессор, профессор кафедры «Информационно-вычислительные системы», ФГБОУ ВПО «Пензенский государственный университет архитектуры и строительства», г. Пенза.
Логанина В.И., д.т.н., профессор, зав. кафедрой «Управление качеством и технологии строительного производства», ФГБОУ ВПО «Пензенский государственный университет архитектуры и строительства», г. Пенза.
Библиографическая ссылка
Гарькина И.А., Данилов А.М., Петренко В.О. РЕШЕНИЕ ПРИБЛИЖЕННЫХ УРАВНЕНИЙ: ДЕКОМПОЗИЦИЯ ПРОСТРАНСТВЕННОГО ДВИЖЕНИЯ УПРАВЛЯЕМОГО ОБЪЕКТА // Современные проблемы науки и образования. – 2014. – № 5. ;URL: https://science-education.ru/ru/article/view?id=14766 (дата обращения: 16.11.2024).