Введение
Традиционно способы остеосинтеза переломов костей делят на четыре группы: накостный остеосинтез, остеосинтез аппаратами внешней фиксации, внутрикостный остеосинтез [7-9].
Фиксацию фрагментов сломанной кости обеспечивают одним из трех способов.
-
Создание внутренней опоры. Например, установка костного аутотрансплантанта или винта, проведенного под суставной поверхностью и создающего опору для неё [7-9].
-
Шунтирование нагрузки. Например, с помощью аппарата внешней фиксации, наложенного на пяточную кость и голень [2].
-
Создание каркасной конструкции, которая воспринимает нагрузку с фиксационных элементов, проведенных через отломки. Например, любые аппараты внешней фиксации, опорные элементы которых проведены только через пяточную кость, пластины, внутрикостные конструкции [7-9].
Мы предложили использовать в травматологии еще один способ противодействия вертикальной нагрузке - создание внутренней преднапряженной конструкции, на основании которой предложен способ армирования внутрисуставных суставных переломов преднапряженными конструкциями (заявка «Способ субхондрального напряженного армирования» № 2013143124 от 23.09.2013 г.) и аппарат аксиальной фиксации для лечения переломов пяточной кости, основанный на этом способе [1; 4-6].
Цель настоящего исследования: путем теоретических расчетов и эксперимента доказать целесообразность преднаряжения спиц при армировании переломов суставных поверхностей костей человека.
Материалы и методы
В качестве модели для эксперимента мы выбрали аппарат аксиальной фиксации (ААФ), устройство которого и особенности его применения изложены в статье «Лечение переломов пяточной кости аппаратом аксиальной фиксации» [1].
ААФ состоит из двух пучков спиц, которые преднапрягают во взаимно-противоположных направлениях при остеосинтезе перелома пяточной кости. Мы решили теоретический расчет выполнить для одной преднапряженной спицы.
Изгиб спиц приводит к образованию точки опоры в различных местах кости в зависимости от анатомии перелома [1].
1. Теоретическое обоснование
1. Вывод зависимости для определения деформированного состояния аппарата фиксации пяточной кости.
Схема нагружения элемента аппарата показана на рис. 1.
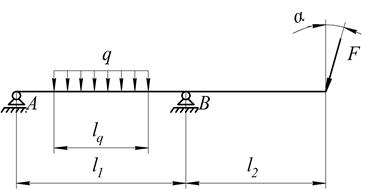
Рис. 1. Расчетная схема нагружения одного элемента аппарата (спицы): 
- распределенная нагрузка; 
- сосредоточенная сила; 
- расстояние между опорами АВ; 
- расстояние между опорой В и сосредоточенной силой; 
- расстояние, на котором приложена распределенная нагрузка; 
- угол приложения сосредоточенной силы.
Целью теоретических исследований является вывод уравнения для определения сосредоточенной силы , при которой вертикальная деформация элемента (спицы) на участке АВ (рис. 1) будет равна нулю.
Методика получения искомой зависимости включает следующие этапы.
На первом этапе исходную схему нагружения на основе принципа независимости действия сил представим как суперпозицию (наложение) двух расчетных схем:
- схема, нагруженная только силой (рис. 2);
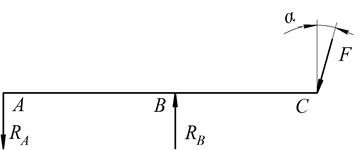
Рис. 2. Схема нагружения сосредоточенной силой
- схема, нагруженная только распределенной нагрузкой (рис. 3).
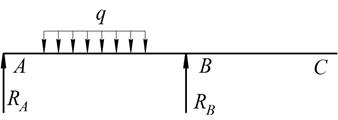
Рис. 3. Схема нагружения распределенной нагрузкой
На втором этапе для каждой схемы построим эпюры изгибающих моментов.
На третьем этапе, из условия равенства площадей эпюр изгибающих моментов, на участке АВ, по первой (рис. 2) и второй (рис. 3) схеме, выведем искомую зависимость.
Теперь рассмотрим каждую схему.
Расчетная схема показана на рис. 4. Для построения эпюры изгибающих моментов необходимо определить реакции в опорах 
и 
и составить уравнения моментов в точках А, В и С.
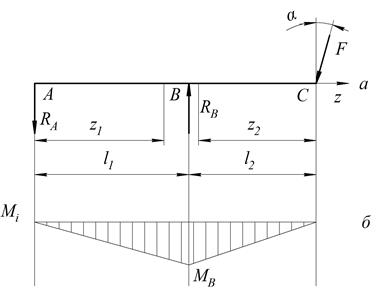
Рис. 4. Расчетная схема от действия силы
Составим уравнения равновесия (рис. 4а), приравняв нулю сумму моментов всех сил относительно точки А и точки В:
(1а)
и 
(1б)
Решая условия (1 а, б) относительно неизвестных составляющих реакций в опорах и , получим:
(2а)
и 
(2б)
Для наглядного представления о характере изменения изгибающих моментов построим эпюру. Чтобы построить эпюру, определим значения моментов, возникающих в точках А, B и С.
Уравнения изгибающего момента (рис. 4).
На первом участке 
:
при 
, 
; (3а)
при 
, 
. (3б)
На втором участке 
:
при 
, 
; (4а)
при 
, 
. (4б)
Из полученных выражений (4) видно, что эпюра моментов на участке АВ будет возрастать, а на участке ВС убывать и примет вид, как на рис. 4б.
Расчетная схема показана на рис. 5. Для построения эпюры изгибающих моментов необходимо определить реакции в опорах и и составить уравнения моментов в точках А, D, Е, G, B и С.
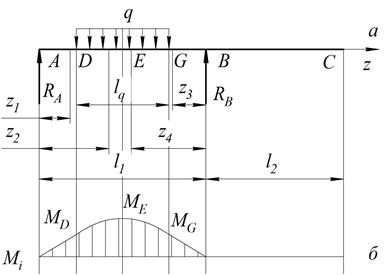
Рис. 5. Расчетная схема от действия распределенной нагрузки
Составим уравнения равновесия (рис. 5а), приравняв нулю сумму моментов всех сил относительно точки А и точки В при действии распределенной нагрузки :
(5а)
и 
(5б)
Решая условия (5 а, б) относительно неизвестных составляющих реакций в опорах и , получим:
(6)
Для наглядного представления о характере изменения изгибающих моментов построим эпюру. Чтобы построить эпюру, определим значения моментов, возникающих в точках А, D, Е, G, B и С.
Составим уравнения моментов, рассматривая элемент аппарата слева направо.
Уравнения изгибающего момента (рис. 5).
На первом участке 
:
при , ; (7а)
при 
, 
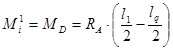. (7б)
На втором участке 
:
при 
, 
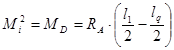; (8а)
при 
, 
. (8б)
Составим уравнения моментов, рассматривая элемент аппарата справа налево.
На третьем участке 
:
при 
, 
; (9а)
при 
, 
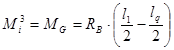. (9б)
На четвертом участке 
:
при 
, 
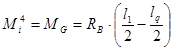; (10а)
при 
, 
. (10б)
Подставив в уравнения моментов (10 а, б) значения реакций опор (6), получим:
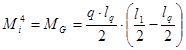; (11а)
. (11б)
Из полученных выражений видно, что эпюра моментов рис. 5б от точки А до точки D прямолинейно возрастает, от точки D до точки G имеет параболическую форму с максимумом в точке Е, далее эпюра имеет прямолинейный нисходящий характер.
Определим площадь эпюры моментов от точки А до точки В, рис. 4б.
(12)
Подставив в выражение (12) значения 
из условия (4б) и преобразовав их, получим:
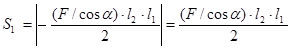(13)
Определим площадь эпюры моментов от точки А до точки В, рис. 5б:
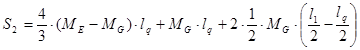(14)
Подставив в выражение (14) значения 
и 
из условий (11 а, б) и преобразовав их, получим:
(15)
Приравняв левые и правые части уравнений (14) и (15), получим равенство площадей эпюр изгибающих моментов:
или
(16)
Решая уравнение (16) относительно , получим функциональную зависимость силы от распределенной нагрузки :
(17)
В элементе аппарата максимальное напряжение, вызванное силой , не должно превышать допустимого значения.
Запишем выражение максимального напряжения при изгибе в элементе аппарата:
, (18)
где 
- максимальное изгибающее напряжение элемента;
- допустимое изгибающее напряжение 
;
- предел прочности материала элемента аппарата;
- момент сопротивления при изгибе, 
Решив уравнение (18) относительно и приравняв 
, получим максимальное значение силы , которое не приведет элемент аппарата к разрушению:
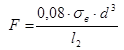(19)
2. Экспериментальная оценка
Для того что бы предложить использовать преднапряженные конструкции в травматологии, нам необходимо доказать, что напряжение элементов конструкции улучшает её фиксационные свойства. Для этого необходимо удостовериться, что напряжение спиц приводит к увеличению коэффициента жесткости конструкции.
Известно, что «жесткость исследуемых чрескостных модулей – это способность оказывать сопротивление смещению отломков, возникающему в результате внешней нагрузки».
Жесткость остеосинтеза характеризуется:
- коэффициентом жесткости (К), который определяется из отношения внешних нагрузок к линейным и угловым перемещениям;
- податливостью, которая определяется из соотношения линейных и угловых перемещений с единичными нагрузками (величина, обратная коэффициенту жесткости).
С этой целью был проведен эксперимент для анализа изменения коэффициента жесткости модели из двух пучков спиц без нагрузки и при различных вариантах нагрузки спиц на упрощенной модели ААФ. Коэффициент жесткости рассчитывали по формуле:
K компр= Fкомпр/U компр (20)
Единица измерения линейных коэффициентов жесткости H/мм [3].
Для этого нами была смоделирована костная система пятки из дерева с заданными геометрическими параметрами, которые не изменяли в ходе эксперимента. Дерево было выбрано как наиболее доступный материал. Нас интересовала жесткость конструкции из напряженных спиц. Механические свойства материала, имитирующего кость, не принимали во внимание. Параметры модели (рис. 6) выбрали на основании анализа рентгенограмм пациентов, пролеченных в стационаре с 2011 по 2014 год при помощи аппарата аксиальной фиксации. Определили следующие размеры.
1. Расстояние от дополнительной точки опоры спиц до переднего фрагмента пяточной кости, в котором происходит пересечение спиц – среднее расстояние = 6.3 см.
2. Расстояние от центра фрагментов суставной поверхности до переднего фрагмента пяточной кости. Среднее расстояние = 3 см.
3. Расстояние от переднего фрагмента до аппарата аксиальной фиксации. Среднее расстояние = 11.5 см.
4. Расстояние от наиболее нижней точки пяточного бугра до переднего фрагмента пяточной кости. Среднее расстояние 6.0 см.
5. Угол между пучками спиц. Средний угол между пучками спиц = 28 градусов. Конструкция (рис. 6) состояла из:
1) деревянного бруска 1, имитировавшего передний фрагмент пяточной кости, в котором пересекаются спицы обоих пучков;
2) прямоугольного бруска 5, который моделировал осколки суставной поверхности пяточной кости. В центре этого бруска было сделано вертикальное овальное отверстие с осью. К этой оси подвешивали груз для имитации вертикальной нагрузки на суставную поверхность пяточной кости и спицы верхнего пучка;
3) деревянной рейки толщиной 3 мм, которая имитировала точку опоры о пяточный бугор;
4) двух спиц верхнего пучка и двух спиц нижнего пучка. Оба пучка спиц проводили, как при остеосинтезе пяточной кости, под углом друг к другу с пересечением в бруске 1. При этом нижний пучок спиц проходил через брусок 3, а верхний был расположен на верхней его части как на точке опоры. Верхний пучок спиц проходил через брусок 5, имитирующий осколки суставной поверхности пяточной кости;
5) под нижним пучком спиц располагали точку опоры, имитирующую точку опоры пяточного бугра о пол при ходьбе человека.
Рис. 6. Модель для эксперимента:
- Брусок-имитация переднего фрагмента пяточной кости.
- Имитация опоры для пяточной кости о пол при ходьбе: опорный брусок с расположенной на нем стальной трубкой диаметром 3 мм.
- Узкий брусок шириной 3 мм, изображающий точку опоры о пяточный бугор.
- Аппарат аксиальной фиксации с поворотными модулями.
- Брусок, изображающий суставную поверхность.
- Индикатор.
- Груз.
Модель позволяла измерить деформацию, возникающую при действии вертикальной смещающей нагрузки при различных вариантах аксиальной фиксации. Для измерения величины возникающей деформации мы использовали индикатор часового типа производства Кировского завода «Красный инструментальщик» по ГОСТ 577-68.
Во всех экспериментах использовали груз 3 кг, который подвешивали к оси деревянного бруска 5. При подвешивании груза возникала деформация спиц верхнего пука, которую мы измеряли при помощи индикатора часового типа. При этом мы сравнили коэффициенты жесткости конструкций при остеосинтезе спицами, аппаратом в статическом варианте, и при различных вариантах напряжения спиц при помощи аппарата аксиальной фиксации.
Зная массу груза, определяли силу F компр., действующую на модель.
Вес тела P - это сила, с которой тело действует на горизонтальную опору или вертикальный подвес под влиянием притяжения Земли. Вес тела имеет направление, как и любая сила, и является величиной векторной. Стрелка, которой обозначают вес тела на рисунках и графиках, всегда направлена вниз, так же как и сила тяжести. В нашем эксперименте F компр= P, где P = m∙g (21)
где m - масса тела,
g - ускорение свободного падения = 9,81 м/с2.
Следовательно, во всех случаях на аппарат аксиальной фиксации действовала сила:
P = 3 кг ∙ 9,81 м/с2 = 29,43 Н.
Исходя из вышеприведенной формулы, коэффициент жесткости в каждом случае определяли как:
К= 29,43(H) / U компр (мм).
Результаты
Проведены следующие эксперименты на ранее описанной модели.
Эксперимент № 1: с дополнительной точкой опоры под нефиксированными спицами (имитирует остеосинтез перелома пяточной кости спицами, при условии, что пяточный бугор цел).
В условиях эксперимента первый пучок спиц проксимально расположен на точке опоры, второй проходит сквозь брусок 3. Такое положение обоих пучков спиц образуем при правильной аксиальной фиксации спицами: верхний пучок расположен на точке опоры (верхней части пяточного бугра), нижний проходит через пяточный бугор в тело пяточной кости.
Результат: деформация (U)=1,50 мм.
К = 29,43/U = 19,62 H/мм.
Эксперимент № 2 со спицами с опорой и аппаратом в статическом режиме. Наружные концы спиц фиксированы аппаратом. Пучки спиц не напряжены. Аналогичная ситуация при остеосинтезе пяточной кости возникнет, если спицы объединить в аппарате внешней фиксации.
Результат U= 1,09 мм.
К = 29.43/1.09 = 27 Н/мм.
Эксперимент № 3 с аппаратом с нагрузкой первого пучка о точку опоры. Путем сближения верхней и нижней части аппарата при помощи стержней выполнили напряжение спиц о брусок (3) как о точку опоры. Подобная ситуация возникает при остеосинтезе пяточной кости аппаратом аксиальной фиксации с напряжением о точку опоры.
Результат: U= 0,74 мм.
К= 29,43/0,74 = 39,8 Н/мм.
Эксперимент № 4 с аппаратом без дополнительной точки опоры.
Мы увеличили расстояние между базами аппарата, перепилив поперечно рейку 3 (рис. 6), являвшуюся точкой дополнительной опоры (имитация сломанного на осколки пяточного бугра).
Результат U = 1,71 мм.
К= 29,43/1,71 = 17,21 H/мм.
Эксперимент № 5 с использованием приёма «изменения угла наклона спиц».
Для этого мы произвели разворот осевого модуля аппарата.
Эксперимент № 6 с нагрузкой на спицы без задней опоры и без аппарата. Такая ситуация возникнет, если выполнить остеосинтез спицами многооскольчатого перелома пяточной кости с разрушенным пяточным бугром.
Для этого мы отсоединили аппарат аксиальной фиксации.
Результат: U = 4,0 мм.
К=29,43/4,0 = 7,4 H/мм.
Эксперимент № 7 со спицами, которые проведены через брусок 3 параллельно (а не под углом друг к другу), нагружены в аппарате и не имеют передней опоры.
Данная ситуация произойдёт при проведении через пяточную кость спиц параллельно. При этом спицы либо вообще не захватят осколки суставной поверхности, либо (если пройдут сквозь них) окажутся в подтаранном суставе и не будут иметь дистально жесткой заделки.
Для этого мы провели оба пучка спиц через брусок 3. Нижний пучок спиц провели через брусок 3 и брусок 1.
Результат: U>15,0 мм (после этого деформация продолжалась, а датчик её больше не фиксировал, так как диапазон измерения индикатора 10 мм).
Измерение линейкой показало, что деформация составила 15 мм, тогда:
К=29,43/15= 1,96 Н/мм.
Путем расчетов получена аналитическая зависимость (17) для расчета сосредоточенной силы , при которой вертикальная деформация элемента (спицы) аппарата на участке АВ (рис. 1) равна нулю.
В случае когда необходимо создать преднапряженное состояние, уравнение (17) с заменой геометрических размеров на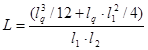 
запишем в виде:
(22)
Прогиб и деформация спицы не произойдут только в тех случаях, когда F ≥ q∙L.
Как показывает практика, не всегда возможно учесть все факторы, влияющие на напряженное состояние элемента, при которых соблюдено равенство полученной функциональной зависимости. Так как при определенных условиях вертикальная нагрузка может увеличиться, нами введено условие преднапряженного состояния элемента, учитывающее физиологические обстоятельства, при которых необходимо создать в элементе дополнительную, превышающую в 
раз силу 
, чтобы избежать искажения всей конструкции в целом с учетом всех факторов, влияющих на пациента.
Для определения преднапряженности элемента аппарата в зависимость (22) введем коэффициент 
, который показывает, насколько уменьшится влияние распределенной нагрузки при увеличении силы в раз, и она примет вид:
(23)
Обсуждение результатов
Наименьший коэффициент жесткости К получен при эксперименте № 7: остеосинтез четырьмя спицами, проведенными аксиально под углом друг к другу и не имеющими дополнительной точки опоры. К = 1.96 H/мм.
Т.е. при таком способе фиксации, с учетом того что при параллельном проведении спиц передние концы их окажутся в подтаранном суставе, деформация их будет наибольшей и продолжится до появления передней опоры спиц. При таком способе проведения спиц невозможно получить преднапряженную конструкцию. Это происходит потому, что напряжение спиц невозможно, так как все они проведены проксимально через один отломок. Кроме того, при помощи такого способа часто не удается фиксировать спицами осколки суставной поверхности. Так как данный способ проведения спиц неэффективен, его при дальнейшем анализе не учитывали.
Для того чтобы сравнить между собой оставшиеся экспериментальные модели, требуется выбрать эталонную модель, для сравнения коэффициента К, которой позволяет выяснить: насколько различны характеристики жёсткости этих моделей при действии вертикальной нагрузки.
В качестве эталона выбраны схемы конструкций, использованные в экспериментах № 6 и № 1, коэффициент их жесткости принят за 100%. В указанных моделях использовали 4 спицы, которые совместно обеспечивали такой коэффициент жесткости. Это значит, что 1 спица обеспечивает примерно 25% от коэффициента жесткости всей конструкции.
Анализ результатов экспериментов с эталонами представлен в таблице 1.
Таблица 1. Анализ результатов экспериментов.
|
№ эксперимента |
К Н/мм |
Сравнение с № 6
|
Сравнение с № 1
|
||
|
В процентах |
Количество необходимых спиц при остеосинтезе по способу № 6 |
В процентах |
Количество необходимых спиц при остеосинтезе по способу № 1 |
||
|
№ 1 |
19.62 |
265 |
11 |
100 |
|
|
№ 2 |
27 |
364 |
15 |
137 |
6 |
|
№ 3 |
39.8 |
537.8 |
22 |
202.9 |
9 |
|
№ 4 |
17.21 |
232.6 |
10 |
|
|
|
№ 5 |
26.8 |
362.2 |
15 |
|
|
|
№ 6 |
7.4 |
100 |
|
|
|
Как видно из таблицы 1, результаты эксперимента свидетельствуют о следующем.
-
В случае применения аппарата аксиальной фиксации при переломах пяточной кости с наличием дополнительной точкой опоры К возрастает примерно на 102,9%, по сравнению с правильной аксиальной фиксацией спицами при том же типе перелома пяточной кости. Т.е. применение аппарата аксиальной фиксации позволяет увеличить жесткость конструкции в 2 раза. По сравнению с вариантом без дополнительной точки опоры под спицами жесткость возрастает на 437,8%, или в 5,4 раза.
-
При применении предлагаемого способа фиксации при варианте перелома без дополнительной точкой опоры жесткость возрастёт на 132,6% по сравнению с фиксацией спицами, но при применении способа с изменением угла наклона спиц К возрастёт на 262,2% по сравнению с фиксацией спицами (как вариант может быть применён способ «создания дополнительной точки опоры»). Т.е. применение аппарата аксиальной фиксации позволяет увеличить К конструкции в 3,6 раза.
Полученная нами зависимость между силой и распределенной нагрузкой q:
(23) означает, что при увеличении силы F в k раз произойдет уменьшение действия q в k раз. Например, при увеличении силы напрягающего устройства в 3 раза действие q уменьшится в 3 раза.
Это доказывает то, что преднапряжение спиц в конструкции является способом противодействия вертикальной нагрузке. Это противодействие тем выше, чем больше усилие напрягающего устройства. Значит, теоретически, армирование суставных поверхностей костей преднапряженными спицами более эффективно, чем армирование ненапряженными спицами. Этот вывод объясняет повышенные фиксационные свойства аппарата аксиальной фиксации и согласовывается с данными проведенного нами эксперимента.
Выводы
-
Получена аналитическая зависимость для определения сосредоточенной силы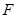, при которой вертикальная деформация элемента (спицы) под действием распределенной нагрузки
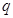на участке АВ (рис. 1) будет равна нулю.
-
В конструкциях, основанных на принципе преднапряженного армирования, имеется зависимость между силой F напрягающего устройства и распределенной нагрузкой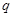. При увеличении силы F напрягающего устройства действие распределенной нагрузки 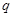уменьшается во столько раз – во сколько возрастает сила F.
-
Проведено экспериментальное исследование, результаты которого подтвердили адекватность аналитических зависимостей как в состоянии, когда на заданном участке отсутствует деформация элемента, так и в состоянии с положительной вертикальной деформацией, которая уменьшает действие нагрузки на элементы конструкции.
-
Напряжение спиц в аппарате аксиальной фиксации приводит к значительному увеличению коэффициента жесткости конструкции.
-
Преднапряженное армирование суставных поверхностей костей при их переломах более эффективно, чем армирование ненапряженными спицами.
Рецензенты:
Астапенков Д.С., д.м.н., профессор кафедры травматологии и ортопедии Государственного бюджетного образовательного учреждения высшего профессионального образования «Южно-Уральский государственный медицинский университет» Министерства здравоохранения Российской Федерации, г. Челябинск.
Анцупов В.П., д.т.н., профессор Федерального бюджетного государственного образовательного учреждения высшего профессионального образования «Магнитогорский государственный технический университет им. Г.И. Носова», г. Магнитогорск.
Библиографическая ссылка
Купитман М.Е., Кургузов С.А., Атманский И.А., Русанов В.А., Русанов В.А. ТЕОРЕТИЧЕСКОЕ И ПРАКТИЧЕСКОЕ ОБОСНОВАНИЕ ЦЕЛЕСООБРАЗНОСТИ АРМИРОВАНИЯ ПЕРЕЛОМОВ СУСТАВНЫХ ПОВЕРХНОСТЕЙ КОСТЕЙ ПРЕДНАПРЯЖЕННЫМИ КОНСТРУКЦИЯМИ // Современные проблемы науки и образования. – 2014. – № 3. ;URL: https://science-education.ru/ru/article/view?id=13327 (дата обращения: 15.11.2024).