Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Бочкарева О.В. 1 Новичкова Т.Ю. 1 Снежкина О.В. 2 Ладин Р.А. 2

---

1 ФГКВОУ ВПО "Пензенский артиллерийский инженерный институт"

2 ФГБОУ ВПО "Пензенский государственный университет архитектуры и строительства"

В статье рассмотрена проблема формирования профессиональных качеств личности будущего строителя путем использования на занятиях по математике профессионально ориентированных задач, адекватных основным видам профессиональной деятельности выпускника. Для реализации представленной концепции авторами использован системный подход к развитию профессиональных качеств, основу которого составляют: понимание взаимосвязи содержания математического образования с содержанием профильных дисциплин (содержательный аспект), формирование умений адекватных основным видам профессиональной деятельности (интеллектуальный аспект), развитие потребности использовать математический аппарат для решения профессиональных задач (мотивационный аспект). Основным средством реализации выделенных качеств являются профессионально ориентированные математические задачи. В статье рассмотрены конкретные примеры, доказывающие действенность и практическую значимость предлагаемой методики, представлена собственная трактовка понятия «профессионально ориентированная математическая задача», сформулированы требования к задачам, проведена их классификация, предложены критерии проверки уровня сформированности профессиональных качеств личности путем решения профессионально ориентированных математических задач различной степени сложности.

Статья в формате PDF

135 KB

профессиональная деятельность

профессиональные качества личности

профессионально ориентированная математическая задача

обучение математике

1. Бочкарева О.В. Профессиональная направленность обучения математике студентов инженерно-строительных специальностей вуза: дис... канд. пед. наук. – Пенза, 2006. – 150 с.

2. Бочкарева О.В., Снежкина О.В., Сироткина М.А. Формирование профессиональных умений на занятиях по математике // Молодой ученый. – 2014. – № 2 (61). – С. 735-738.

3. Карпов В. В., Коробейников А. В. Математические модели задач строительного профиля и численные методы их исследования. – М.; СПб., 1999. – 188 с.

4. Ладин Р.А., Снежкина О.В., Бочкарева О.В., Титова Н.В. Математика и междисциплинарные связи // Молодой ученый. – 2014. – № 1. – С. 550-552.

5. Саранцев Г. И. Упражнения в обучении математике. – М.: Просвещение, 2005. – 256 с.

6. Сироткина М.А., Бочкарева О.В., Снежкина О.В. К вопросу о профессиональной направленности обучения математике // Вестник магистратуры. – 2014. – № 2 (29). – С. 59-61.

7. Снежкина О.В., Левова Г.А., Бочкарева О.В., Ладин Р.А. О роли регионального компонента при преподавании дисциплин математического цикла // Новый университет. Серия: Актуальные проблемы гуманитарных и общественных наук. – 2013. – № 11-12 (32-33). – С. 17-20.

8. Ямбогло И.И., Бочкарева О.В., Снежкина О.В. Некоторые аспекты обучения иностранных студентов в российских вузах // Вестник магистратуры. – 2014. – № 1 (28). – С. 25-27.

Проблема формирования профессиональных качеств личности была и остается одной из актуальных в строительном вузе. Немаловажную роль играет в этом и математика. Обучение и развитие личности в математике, как известно, осуществляется через решение задач. Задачи могут выступать в качестве: носителя действий, адекватных содержанию математики; средства целенаправленного формирования знаний, умений, навыков; способа организации и управления учебно-познавательной деятельностью студентов; одной из форм реализации методов обучения; средства связи теории с практикой [5]. В частности, использование в обучении математике бакалавров по направлению «Строительство» профессионально ориентированных задач позволяет формировать у будущих специалистов необходимые профессиональные качества.

В профессионально ориентированной задаче в качестве задачной ситуации выступает некая модель профессиональной ситуации, в которой по известным характеристикам профессионального объекта или явления надо найти другие его характеристики или свойства. Разрешение или исследование представленной профессиональной ситуации способствует развитию у субъекта определенных профессиональных качеств. Таким образом, профессионально ориентированная математическая задача – это задача, условие и требование которой определяют собой модель некоторой ситуации, возникающей в профессиональной деятельности строителя, а исследование этой ситуации средствами математики способствует профессиональному развитию личности студента [1,2].

Среди профессионально ориентированных математических задач, используемых в строительной практике, наибольшее распространение получили задачи на расчет прочности, устойчивости и колебаний элементов строительных конструкций и сооружений (математические модели в виде систем линейных уравнений), исследование напряженно- деформированного состояния стержней, пластин и оболочек (математические модели в виде дифференциальных уравнений и их систем), нахождение оптимального расхода материалов, ресурсов, сырья (математические модели задач линейного программирования); проведение экспериментальных исследований (например, создание новых строительных материалов) [3,4]. Также широкое применение в строительстве нашли такие разделы математики, как теории функций, площадей поверхностей и объемов геометрических тел, гармонического анализа, численных методов, элементов линейной алгебры и аналитической геометрии, теории вероятностей и математической статистики.

Представленные классификации профессионально ориентированных задач охватывают достаточно большой спектр приложений математики в строительной отрасли. Но эти классификации в недостаточной мере ориентированы на основные виды профессиональной деятельности будущего строителя.

В этой связи мы предлагаем провести следующую классификацию профессионально ориентированных математических задач строительного профиля: проектно-конструкторские, организационно-управленческие, производственно-технологические, исследовательские задачи.

К проектно-конструкторским относятся задачи, отражающие применение математических средств при проведении исследований в области проектирования объектов строительства.

Пример задачи. Необходимо спроектировать план застройки массива десятью домами, причем домов первого типа должно быть три, второго типа – пять, третьего типа – два. Сколько вариантов плана можно представить?

Организационно-управленческие задачи касаются вопросов, связанных с использованием математического аппарата в процессе подготовки производственных отчетов, принятия управленческих решений, осуществления контроля за производством и качеством строительных объектов.

Пример задачи. Завод ЖБИ выпускает декоративные плиты двух типоразмеров – и , затрачивая цветные минеральные наполнители (ЦМН) и цветные минеральные заполнители (ЦМЗ), единовременные ресурсы которых ограничены; доход от реализации продукции и различен (табл. 1). Необходимо найти объем производимых плит, чтобы доход завода был максимален.

Таблица 1

Производственно-технологические задачи демонстрируют применение математических знаний при возведении, ремонте и реконструкции зданий, сооружений и строительных конструкций.

Пример задачи. Для придания консоли жесткости используются две опоры и (рисунок 1), где . Наибольшая жесткость конструкции достигается при наибольшей величине угла , тангенс которого определяется формулой: . Определите, на каком расстоянии от точки следует закрепить опоры, чтобы придать конструкции наибольшую жесткость.

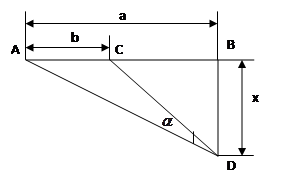
Рис.1. Схема опирания консоли

Исследовательские задачи связаны с использованием математических методов при выполнении экспериментальных и теоретических исследований в области строительства и других отраслей, связанных со строительством.

Пример задачи. По опытным данным зависимости водопоглощенияот температуры обжига Т (табл. 2) определить водопоглощение для промежуточного значения Т=1250С.

Таблица 2

Заметим, что представленные задачи направлены не только на развитие у студентов умений, адекватных основным видам профессиональной деятельности, но и на формирование представления о взаимосвязи содержания математических разделов с профессиональными дисциплинами и строительными отраслями. В процессе решения задач показывается профессионально-практическая значимость математических знаний, что способствует развитию профессиональной мотивации при обучении математике. Все вышеперечисленное позволяет рассматривать профессионально ориентированные задачи как средство формирования профессиональных качеств личности бакалавра-строителя [6,7,8].

Проведенный анализ решения профессионально ориентированных математических задач позволяет выделить следующие уровни сформированности профессиональных качеств.

Первый уровень обеспечивается решением задач на основе использования математического понятия или формулы.

Пример задачи. Координаты центра тяжести панели образуют трехмерный вектор а(150;30;120). Определить координаты центра тяжести этой панели при уменьшении ее геометрической модели в десять раз. Найти расстояние от угла панели до ее центра тяжести.

Решение задачи основано на использовании понятия коллинеарности векторов и формулы для вычисления длины вектора.

Второй уровень обеспечивается решением задач, требующим применения того или иного математического метода.

Пример задачи. Система канонических уравнений для двухэтажной однопролетной статически неопределимой рамы, нагруженной горизонтальной узловой нагрузкой, имеет вид:

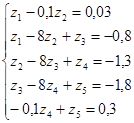
где – искомые угловые перемещения жестких узлов рамы. Раскрыть статическую неопределимость рамы.

На примере данной задачи демонстрируется применение метода Гаусса к решению систем линейных алгебраических уравнений.

Третий уровень обеспечивается решением задач, предполагающим использование аппарата различных математических разделов и аппарата смежных дисциплин (физики, механики, химии и др.).

Пример задачи. Свободно висящий на крюке строительного крана трос соскальзывает с него под действием силы тяжести (трением можно пренебречь). Определить, за какое время соскользнет с крюка весь трос, если в начальный момент трос покоился, а длина троса с одной стороны крюка была равна 10 м, с другой – 8 м.

При составлении математической модели представленной задачи используется знание законов физики, а при исследовании модели – аппарат теории дифференциальных уравнений и линейной алгебры.

Вышесказанное позволяет нам сформулировать требования, предъявляемые к профессионально ориентированным задачам, используемым в рамках математической подготовки бакалавров по направлению «Строительство»:

1) задача должна описывать ситуацию, возникающую в профессиональной деятельности бакалавра-строителя;

2) в задаче должны быть неизвестны характеристики некоторого профессионального объекта или явления, которые надо исследовать субъекту по имеющимся известным характеристикам с помощью средств математики;

3) решение задач должно способствовать прочному усвоению математических знаний, приемов и методов, являющихся основой профессиональной деятельности бакалавра-строителя;

4) задачи должны обеспечить усвоение взаимосвязи математики с общетехническими и специальными дисциплинами;

5) содержание задачи и ее решение требуют знаний по специальным предметам;

6) содержание профессионально ориентированной математической задачи определяет пропедевтический этап изучения понятий специальных дисциплин;

7) решение задач должно обеспечивать математическое и профессиональное развитие личности бакалавра-строителя.

В заключение хотелось бы отметить, для того чтобы профессионально ориентированные математические задачи в должной мере служили средством формирования профессиональных качеств личности бакалавра-строителя, необходимо организовать их систематическое и целенаправленное использование в процессе обучения математике.

Рецензенты:

Усманов В.В., д.п.н., профессор, первый проректор, проректор по научной работе, ФГБОУ ВПО «Пензенский государственный университет архитектуры и строительства», Пенза.

Гарькина И.А., д.т.н., профессор, зам. зав кафедрой «Математика и математическое моделирование», ФГБОУ ВПО «Пензенский государственный университет архитектуры и строительства», Пенза.

Библиографическая ссылка